Trust Region Policy Optimization

Trust region policy optimization(TRPO)는 그 이름에서 드러나듯 최적화 방식 중 trust region방법에 기반한 방식이다. 따라서 최적화의 step size를 “적절"하게 조절해주는 방법임을 추론해볼 수 있다.

Abstract

이 논문에서는 Trust Region Policy optimization(TRPO)이라는 정책 최적화 방법론을 제시한다. 이 방법은 학습과정에서 개선이 보장됨(monotonic improvement)이 증명된 방법이라는데 의의가 있다. 다만, 이론적으로는 매 학습마다 개선이 보장되지만 실제 강화학습의 문제에 적용하기에는 현실적으로 불가능한 제약이 있어 실제 문제 적용에 있어서는 이론적으로 개선이 보장된 방법이 아니라 이를 근사한 방법을 사용하게 된다. TRPO는 natural policy gradient에 뿌리를 두고 있으며 practical algorithm에서 제시하는 풀이방법도 상당부분을 공유한다.

Introduction

저자는 policy optimization 방법을 다음 기준에 따라 세가지로 나눈다.

• Policy Iteration Method

  MDP의 dynamics를 알고 있다면 쉽게 적용할 수 있는 방법이다. Policy evaluation과 policy improvement를 반복하는 방식으로 dynamic programming의 기본적인 방법 중 하나이다.

• Policy Gradient Method

  Policy를 직접 학습시키는 방식으로 value-based 방식과는 다르게 stochastic한 접근을 할 수 있고 연속적인 action space에 대해서도 적용가능한 장점이 있다. Policy gradient theorem을 기반으로 한 방법들이 존재하며 분산이 큰 문제가 있어 분산을 줄이면서 학습하는 방법들이 고안되고 있다.

• Derivative-free optimization Method

  이름 그대로 미분없이 학습하는 방식이다. 논문에서 언급한 cross-entropy method를 예로 들면 다음과 같다. Policy network가 있고 정해진 평균과 분산에 의해 network의 weight 후보들을 뽑아낸다. 100개의 weight set을 뽑았다고 해보자. 그러면 같은 분포에서 sampling한 100개의 다른 weight을 가진 policy network를 갖게 된다. 각각의 network를 활용해 episode를 진행하고 return을 기준으로 성능이 좋은 network를 선택한다. 예를 들어 상위 10%를 정했다고 해보자. 상위 10개의 network를 뽑아내고 이 10개의 network의 평균과 분산을 구한다. 이 새로 구한 평균과 분산으로 다시 100개의 weight set을 뽑고 줄세우는 과정을 반복하면 더 좋은 policy로 수렴하게 될 것이라는게 CEM의 원리이다.

논문에서 제시한 TRPO는 objective function을 직접 최적화하는 것이 아닌 surrogate objective를 최적화하는 방식으로 접근하며(second-order optimization) 무엇보다도 매 학습과정에서 정책의 향상이 보장되는 튼튼한 이론적 토대를 갖는 방법이다. 매 학습과정에서 향상됨을 증명하는 과정이 main contribution이다보니 다른 논문대비 사용되는 수학의 난이도가 높다.

Preliminaries

Preliminaries에서는 논문에서 사용되는 주요 식들을 정리한다. 순서대로 살펴보자.

$$\begin{aligned} \eta(\pi)&=\mathbb{E}_{s_{0}, a_{0}, \ldots}\left[\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}\right)\right], \text { where } \cr s_{0} &\sim \rho_{0}\left(s_{0}\right), a_{t} \sim \pi\left(a_{t} \mid s_{t}\right), s_{t+1} \sim P\left(s_{t+1} \mid s_{t}, a_{t}\right) \end{aligned}$$

우선 $\eta$는 discounted reward의 합에 대한 기대값으로 return이다. 여기서 중요한 것은 $\eta$함수 안에 인자가 $\pi$로 정책이라는 것이다. 따라서 $\eta(\pi)$는 정책 $\pi$를 사용했을 때 얻는 return으로 이 정책을 최대화하는 것이 목표임을 짐작해볼 수 있다. $\rho$는 초기상태의 분포로 이 분포에서 초기상태 $s_{0}$를 sampling하게된다. 행동은 정책함수 $\pi$에 의해 samping되며 마지막 $P$는 state-transition probability로 환경의 dynamics에 의해 결정된다. 쉽게 생각하면 현재 상태 $s_{t}$에서 행동 $a_{t}$를 했을 때 $s_{t+1}$이 될 확률이다.

다음으로는 강화학습에서 통상 사용되는 행동가치, 상태가치 그리고 advantage를 정리한다.

$$ \begin{aligned} Q_{\pi}\left(s_{t}, a_{t}\right)&=\mathbb{E}_{s_{t+1}, a_{t+1}, \ldots}\left[\sum_{l=0}^{\infty} \gamma^{l} r\left(s_{t+l}\right)\right] \cr V_{\pi}\left(s_{t}\right)&=\mathbb{E}_{a_{t}, s_{t+1}, \ldots}\left[\sum_{l=0}^{\infty} \gamma^{l} r\left(s_{t+l}\right)\right] \cr A_{\pi}(s, a)&=Q_{\pi}(s, a)-V_{\pi}(s), \text { where } \cr a_{t} &\sim \pi\left(a_{t} \mid s_{t}\right), s_{t+1} \sim P\left(s_{t+1} \mid s_{t}, a_{t}\right) \text { for } t \geq 0 \end{aligned} $$

여기까지는 강화학습의 기본적인 개념이고 이제부터 본격적으로 이 논문과 관련된 수식이 등장하게 되는데 이 논문 전반의 아이디어는 Kakade & Langford의 논문과 깊이 연결되어 있다.

$$\tag{1} \eta(\tilde{\pi})=\eta(\pi)+\mathbb{E}_{s_{0}, a_{0}, \cdots \sim \tilde{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t} A_{\pi}\left(s_{t}, a_{t}\right)\right]$$

하나씩 살펴보자. 우선 $\tilde{\pi}$와 $\pi$는 각각 다른 정책이다. 이 식에서 말하는 바는 정책 $\tilde{\pi}$의 expected return은 다른 정책 $\pi$에 대한 식으로 표현이 가능하다는 것이며 $\pi$의 expected return과 $\tilde{\pi}$에서 sampling한 trajectory에서 $\pi$에 대해 discounted advantage의 합에 대한 기대값을 더하면 $\tilde{\pi}$의 expected return을 구할 수 있다는 것이다. 다른 정책의 expected return을 구하는데 심지어 다른 정책에서 뽑아낸 trajectory를 따라가며 현재 정책의 discounted advantage합의 기대값에 현재 정책의 expected return을 더하면 같아진다니 신기한 일이 아닐 수 없다. 이에 대한 증명은 Appendix A에 첨부되어 있으며 간단한 MDP를 그려서 해보아도 위 식이 성립하는 것을 확인해 볼 수 있다.

이어서 이후 식 전개를 위해 discounted visitation frequency $p_{\pi}$를 정의한다.

$$\rho_{\pi}(s)=P\left(s_{0}=s\right)+\gamma P\left(s_{1}=s\right)+\gamma^{2} P\left(s_{2}=s\right)+\ldots$$

정책 $\pi$에서 상태 $s$의 discounted frequency는 초기 상태 $s_{0}$가 $s$을 확률, $s_{1}$이 $s$일 확률에 discount가 곱해진 값, 그리고 그 다음상태에서 $s$일 확률에 discount factor의 제곱이 곱해진 값과 같은 형태로 누적합을 해주면 얻을 수 있다. Dicsount factor가 곱해진 것을 확률을 현재시점으로 환산한다고 바라보면 (마치 은행 복리개념처럼) 정성적으로는 정책 $\pi$를 따를 때 상태 $s$에 있을 확률이라고 볼 수 있다.

이렇게 visitation frequency를 정의한 이유는 바로 (1)의 식을 다음과 같이 바꾸어 표현하기 위함이다.

$$\tag{2} \begin{aligned} \eta(\tilde{\pi}) &=\eta(\pi)+\sum_{t=0}^{\infty} \sum_{s} P\left(s_{t}=s \mid \tilde{\pi}\right) \sum_{a} \tilde{\pi}(a \mid s) \gamma^{t} A_{\pi}(s, a) \cr &=\eta(\pi)+\sum_{s} \sum_{t=0}^{\infty} \gamma^{t} P\left(s_{t}=s \mid \tilde{\pi}\right) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a) \cr &=\eta(\pi)+\sum_{s} \rho_{\tilde{\pi}}(s) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a) \end{aligned} $$

우선 (1)과 비교해보면 첫번째줄에서 $\tilde{\pi}$에서 samping한 trajectory의 기대값이 $\sum_{s} P\left(s_{t}=s \mid \tilde{\pi}\right) \sum_{a} \tilde{\pi}(a \mid s)$로 표현되었음을 볼 수 있다. (2)과정에서 이루고자 하는 바는 시간의 summation을 잘 처리해서 상태와 행동의 summation으로 바꾸는 것이다. 첫번째 줄에서 advantage term까지 같이 보고 생각하면 이해하기가 더 수월하다. $\sum_{t=0}^{\infty}$ 오른쪽 전체를 보면 정책 $\tilde{\pi}$일 때 모든 상태와 해당 정책에 의해 결정된 행동들에 대한 advantage의 합으로 advantage 앞쪽은 확률이므로 기대값이 전개된 것으로 볼 수 있다. 그 다음 줄 부터는 timestep $t$와 관련된 term을 몰아주어 앞서 정의한 discounted visitation frequency로 바꾸어 표현한다.

여기서 중요한 아이디어가 등장한다. 앞에서 $\tilde{\pi}$와 $\pi$를 각각 다른 정책이라고 했었다. $\eta(\tilde{\pi})$가 update된 정책, $\eta(\pi)$가 현재 정책이라고하면, $\sum_{s} \rho_{\tilde{\pi}}(s) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)$에서 $\sum_{s} \rho_{\tilde{\pi}}(s)$는 visitation frequency로 어차피 양수이므로 $\sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a) \geq 0$만 만족하면 정책의 성능인 $\eta$가 향상되거나 최소 유지됨을 알 수 있다.

그렇다면 $\tilde{\pi}(s) = \argmax_{a} A_{\pi}(s, a)$와 같이 새로운 정책을 advantage를 크게하는 action으로 정책을 잡아볼 수 있다. (이는 policy iteration방법에서 policy improvement과정에 greedy policy를 하는 것에 비유할 수 있다) 그렇다면 단 하나의 state-action pair라도 양수인 advantage를 가지면 성능 유지(visitation이 0인 경우) 또는 향상을 보장하기에 optimal policy를 향해 나아갈 수 있게 된다. 여기까지는 좋은데 현실적으로 심각한 문제가 발생하게 된다. 우선 우리가 얻게되는 advantage는 실제 advantage가 아니라 추정하는 값으로 항상 오차를 가지고 있을 것이기 때문에 음수가 발생할 수 있으며 다른 하나는 $\pi$를 향상 시켜야 하는데 visitation frequency를 보면 update된 정책인 $\tilde{\pi}$의 visitation frequency를 사용해야 한다는 것이다.

이제 슬슬 왜 이 방법의 이름이 trust region을 갖는지에 대한 단서가 등장한다. 이러한 문제를 풀기위해 새로운 local approximation을 다음과 같이 도입한다.

$$\tag{3} L_{\pi}(\tilde{\pi})=\eta(\pi)+\sum_{s} \rho_{\pi}(s) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)$$

Visitation frequency를 update된 정책으로 사용하지 않고 현재 정책을 사용하고 있음을 볼 수 있다. 이 부분은 정책변화에 대한 visitation frequency 변화를 무시하겠다는 뜻이다. 현실적으로 미래 정책의 visitation frequency를 쓸 수는 없으므로 어쩔 수 없는 타협으로 볼 수 있다. 만약 사용하는 정책이 neural network처럼 parameterized policy $\pi_{\theta}$로 미분가능하다면 $L_{\pi}$는 parameter $\theta_{0}$ 근방에서 1차근사를 해볼 수 있다. (Local approximation)

$$\tag{4} \begin{aligned} L_{\pi_{\theta_{0}}}\left(\pi_{\theta_{0}}\right) &=\eta\left(\pi_{\theta_{0}}\right) \cr \left.\nabla_{\theta} L_{\pi_{\theta_{0}}}\left(\pi_{\theta}\right)\right|_{\theta=\theta_{0}} &=\left.\nabla_{\theta} \eta\left(\pi_{\theta}\right)\right|_{\theta=\theta_{0}} \end{aligned} $$

위 식은 $\theta_{0}$에서 1차근사를 한 식임을 알 수 있다. 다시 말해 $\theta_{0}$ 근방에서 $L_{\pi_{\theta_{\text{old}}}}$를 향상시키는 $\pi_{\theta_{0}} \rightarrow \tilde{\pi}$는 $\eta$도 향상시킴을 의미한다. 하지만 1차근사가 갖는 단점이 어디가지는 않는다. Update를 해야하는 방향은 알 수 있으나 한 step에서 얼마만큼 update를 해야하는지에 대해서는 알 수가 없다.

여기서 다시 Kakade & Langford (2002)가 제시한 방법을 사용하는데, 이 방법의 이름이 conservative policy iteration, 즉 보수적인 정책반복법이다. 이 방법은 $\eta$를 향상시키기는데 필요한 explicit lower bounds를 제시한다.

식(5)에서는 다음과 같은 mixture policy를 보여주는데 현재 정책이 $\pi_{\text{old}}$, 앞서 local approximator에서 얻을 수 있는 가장 좋은 정책을 $\pi^{\prime}=\arg \max _{\pi^{\prime}} L_{\pi_{\text {old }}}\left(\pi^{\prime}\right)$라고 하고 다음과 같이 $\pi_{\text{new}}$를 정의한다.

$$\tag{5} \pi_{\text {new }}(a \mid s)=(1-\alpha) \pi_{\text {old }}(a \mid s)+\alpha \pi^{\prime}(a \mid s)$$

Kakade & Langford는 위의 식에 대해서 다음의 lower bound를 유도하였다.

$$\tag{6} \begin{aligned} \eta\left(\pi_{\text {new }}\right) & \geq L_{\pi_{\text {old }}}\left(\pi_{\text {new }}\right)-\frac{2 \epsilon \gamma}{(1-\gamma)^{2}} \alpha^{2} \cr \text { where } \epsilon&=\max _{s}\left|\mathbb{E}_{a \sim \pi^{\prime}(a \mid s)}\left[A_{\pi}(s, a)\right]\right| \end{aligned} $$

Lower bound를 알았으니 저 lower bound를 높이는 방식을 찾으면 된다고 생각할 수 있지만 일단 식 (5)는 실제로 쓰기가 매우 어려운 형태이다. $\pi^{\prime}$을 보면 local approximator를 가장 크게 하는 $\pi$를 잡아야 하는데 이 자체도 어려울 뿐더러 $\pi_{\text{new}}$는 mixture policy이므로 이렇게 구하기도 힘든 $\pi^{\prime}$을 섞어쓰기까지 해야한다. 게다가 $\epsilon$을 보면 정책 $\pi^{\prime}$을 사용할 때 모든 $\pi$의 모든 상태에 대해서 가장 큰 advantage를 사용하도록 되어있는데 “모든 상태에 대해서 최대"라는 말이 상태공간의 크기를 생각할 때 현실적으로 계산하기 어려울 것임을 알 수 있다.

Preliminaries에서는 이러한 문제를 제기하고 실용적으로 사용할 수 있는 정책향상방법이 필요함을 언급한다.

Monotonic Improvement Guarantee for General Stochastic Policies

Policy iteration방법은 정책을 평가하고 평가된 정책을 이용해 정책개선(greedy action selection 등)을 사용하는 방법이다. 즉 정책평가와 정책개선을 반복하며 control문제를 푸는 방식이다. (6)의 improvement bound를 잘 확장하면 policy iteration으로 control 문제를 풀 수 있게 된다는 아이디어를 갖고 다음의 확장이 이루어 진다.

우선 mixture policy는 언급한대로 쓰기가 어렵다. 대게 우리는 stochastic policy를 사용하게 된다. 따라서 섞어쓰는 비율인 $\alpha$를 $\pi$와 $\tilde{\pi}$의 distance measure로 바꾸어 쓰게된다. Distance measure가 작다면 improvement bound도 작게 움직일 것이고 distance measure가 크다면 improvement bound도 크게 움직일 것이므로 직관과도 일치한다. 그렇다면 남은 문제는 distance measure로 뭘 쓸가 인데 논문에서는 total variantion divergence라는 개념을 distance measure로 도입한다. 정의는 다음과 같다.

$$ D_{\mathrm{TV}}(p | q)=\frac{1}{2} \sum_{i} \lvert p_{i}-q_{i} \rvert $$

분포차이를 계산하는 아주 단순한 식이다. 확률분포에서 $i$번째 값에 대해 차이의 중간지점들을 합한것이다. 그리고 이 분포에서 최대로 다른 정도를 $D_{\mathrm{TV}}^{\max}(\pi, \tilde{\pi})$라고 하고 다음과 같이 정의한다.

$$ D_{\mathrm{TV}}^{\max }(\pi, \tilde{\pi})=\max _{s} D_{T V}(\pi(\cdot \mid s) | \tilde{\pi}(\cdot \mid s)) $$

모든 상태에 대해서 가장 정책의 확률차이가 클 때의 중간값으로 해석할 수 있다. 말 그대로 total variance divergence의 최댓값이다.

여기서 논문은 다음의 정리를 제시한다.

위에 대한 증명은 논문 appendix에 첨부되어 있다. 일단 (8)과 (6)은 거의 같은 form을 가지며 $\alpha$와 $\epsilon$의 의미가 달라진 것이 차이이다. 여기서 bound는 다음의 관계에 의해 더 바뀔 수 있다.

$$ D_{T V}(p \mid q)^{2} \leq D_{\mathrm{KL}}(p \mid q) $$

Total variance에서와 마찬가지로 KL divergence에 대해서도 최댓값을 적용하면 $D_{\mathrm{KL}}^{\max }(\pi, \tilde{\pi})=\max _{s} D_{\mathrm{KL}}(\pi(\cdot \mid s) | \tilde{\pi}(\cdot \mid s))$와 같이 쓸 수 있고 Theorem 1은 다음과 같이 바뀐다.

$$\tag{9} \begin{aligned} \eta(\tilde{\pi}) & \geq L_{\pi}(\tilde{\pi})-C D_{\mathrm{KL}}^{\max }(\pi, \tilde{\pi}) \cr & \text { where } C=\frac{4 \epsilon \gamma}{(1-\gamma)^{2}} \end{aligned} $$

(9)의 policy improvement bound를 사용하여 policy iteration에 적용하면 논문에서 제시하는 Algorithm 1이 된다.

Pseudocode를 따라가보자. 정책을 초기화한 뒤, convergence 조건이 만족될 때까지 반복문을 돌게 된다. 앞서 policy iteration은 정책평가와 정책개선을 반복적으로 사용하는 방법이라고 언급했었는데, 모든 advantage를 계산하는 이 부분이 정책평가에 해당한다. 사실, 이 과정은 모든 state-action pair에 대한 연산을 하는 과정으로 연산량이 어마어마하게 많은 작업임을 염두에 두자. 바로 다음내용은 정책개선으로 (9)를 이용해서 개선된 정책 $\pi_{i+1}$을 구하는 과정이다. 이를 계속 반복하게되면 expected return이 단조증가하도록 할 수 있는 Algorithm 1이 완성된다.

단조증가하는 정책이므로 $\eta\left(\pi_{0}\right) \leq \eta\left(\pi_{1}\right) \leq \eta\left(\pi_{2}\right) \leq \ldots$와 같이 쓸 수 있으며 $M_{i}(\pi) = L_{\pi_i}(\pi) - CD_{\mathrm{KL}}^{\max}(\pi_{i}, \pi)$라고 하면 다음이 성립한다.

$$\tag{10} \begin{aligned} &\eta\left(\pi_{i+1}\right) \geq M_{i}\left(\pi_{i+1}\right) \text { by Equation (9) }\cr &\eta\left(\pi_{i}\right)=M_{i}\left(\pi_{i}\right), \text { therefore }\cr &\eta\left(\pi_{i+1}\right)-\eta\left(\pi_{i}\right) \geq M_{i}\left(\pi_{i+1}\right)-M\left(\pi_{i}\right) \end{aligned} $$

위 식에 의해서 surrogate인 $M_{i}$를 매 iteration에서 최대화하게되면 $\eta$함수를 감소하지 않도록 만들 수 있는 것과 동치이며 이는 minorization-maximization (MM) algorithm의 한 종류이다. 즉 기대 return함수 $\eta$를 최대화해야하는데 이 최대화해야하는 대상 $\eta$의 lower bound를 알고 있으므로 이 lower bound를 최대화하면 $\eta$도 같이 최대화하는 원리이다. $M_{i}$가 $\pi_{i}$에서 $\eta$를 최소화하는 surrogate function으로 사용되었다. 따라서 $M_{i}$를 최대화하면 원래 목적인 $\eta$의 최대화도 달성할 수 있다.

이론적으로 Algorithm 1은 개선을 보장하는 학습방법이라는 의의가 있으나 앞서 언급한 내용으로 인해 현실적인 적용이 매우 어렵다. 따라서 다음 section에서 소개하는 Trust region policy optimization(TRPO)는 Algorithm 1의 approximation으로 KL divergence를 Algorithm 1에서 처럼 penalty로 사용하는 것이 아닌 제약조건으로 사용함으로써 매 iteration의 update양을 늘려 현실적으로 쓸 수 있는 방법으로 만들어준다.

Optimization of Parameterized Policies

정책평가과정에서 모든 상태에 대해 정책을 평가하는 것은 현실적으로 어렵다. 위의 Algorithm 1은 이론적으로 가능할 뿐 현실세계에 적용하기 위해서는 유한한 sample과 임의의 parameterization에 대해 사용가능해야 한다.

정책에 대한 임의의 parameterization은 $\pi_{\theta}(a \mid s)$와 같이 $\theta$에 대한 함수로 정책을 만들면 된다. 여기서 저자는 편의를 위해 notation을 바꾸는데 여기서부터 사용되는 $\theta$는 모두 정책에 대한 parameterization이다.

$$ \begin{aligned} \eta(\theta) &\coloneqq \eta(\pi_{\theta}) \cr L_{\theta}(\tilde{\theta}) &\coloneqq L_{\pi_{\theta}}(\pi_{\tilde{\theta}}) \cr D_{\mathrm{KL}}(\theta \Vert \tilde{\theta}) &\coloneqq D_{\mathrm{KL}}(\pi_{\theta} \Vert \pi_{\tilde{\theta}}) \end{aligned} $$

$\theta_{\mathrm{old}}$도 마찬가지로 이전 정책의 parameterization이다.

위의 notation으로 식 (9)를 쓰면 $\eta(\theta) \geq L_{\theta_{\mathrm{old}}}(\theta) - CD_{\mathrm{KL}}^{\mathrm{max}}(\theta_{\mathrm{old}}, \theta)$이며 등호는 $\theta = \theta_{\mathrm{old}}$일때 성립한다. 따라서 다음의 maximization을 통해 $\eta$를 개선할 수 있다.

$$\underset{\theta}{\operatorname{maximize}}\left[L_{\theta_{\mathrm{old}}}(\theta)-C D_{\mathrm{KL}}^{\max }\left(\theta_{\mathrm{old}}, \theta\right)\right]$$

사실 여기까지는 앞의 식을 notation만 바꿔서 쓴 것에 불과하다. 이제 문제를 해결하기 위해 maximization문제를 제한조건있는 최적화(constrained optimization)으로 바꾸어 풀게된다.

위 식에서 사용된 $C$는 (9)에서 언급된 것 처럼 $\frac{4 \epsilon \gamma}{(1-\gamma)^{2}}$이다. 들어가는 숫자를 생각해보면 $\epsilon$은 지금 advantage 최대값으로 모든 상태에서의 advantage를 계산하게 만든 장본인이고 $\gamma$는 discount factor인데 보통 discount factor는 0.99, 0.95 이런 값들을 주지 갑자기 0.01로 discount를 하지는 않는다. 따라서 $C$의 값이 엄청나게 큰 값이 될 것임을 짐작할 수 있다. $C$는 의미상 penalty에 해당하는데 penalty가 이렇게 크게 들어가다보니 정작 학습의 step size가 너무 작아져서 $\theta_{\mathrm{old}}$에서 $\theta$로의 변화가 미미하게 되고 학습이 잘 되지 않는 문제가 발생한다. 따라서 지금까지 섬세하게 이론적인 토대를 구축한거에 비해서 다소 과감한 문제변형을 하는데 바로 hard constraints를 사용한 제한조건 최적화로의 변경이다.

$$\tag{11}\begin{aligned} &\underset{\theta}{\operatorname{maximize}} L_{\theta_{\text{old}}}(\theta) \cr &\text{ subject to } D_{\mathrm{KL}}^{\max }\left(\theta_{\text{old}}, \theta\right) \leq \delta \end{aligned}$$

$L_{\theta{\text{old}}}$을 최대화하면서 $D_{\mathrm{KL}}^{\max}$를 hard constraints인 $\delta$보다 작거나 같은 조건을 만족하는 최적화로 바꾼 것이다. 여기서 TRPO의 TR, 즉 trust region이 등장한다. $L$을 최대화하되, 무작정 크게하면 단조 증가가 보장되는 범위를 넘어설 수도 있으므로 이전 정책과 현재 정책의 차이가 $\delta$를 넘지 않은 선에서 최대화하는 문제로 변형한 것이다. Hard constraints로 사용된 이 $\delta$가 바로 trust region, 즉 정책 개선이 보장되는 믿을 수 있는 영역을 의미하는 것이다.

하지만 여전히 문제는 남아있다. $D_{KL}$도 쉬운 연산이 아니다. 모든 상태에 대해서 확률분포 상 최대의 KL Divergence를 계산하는 것 또한 만만한 연산이 아니다. 여기서는 heuristic하게 다음과 같은 average KL divergence를 사용해 문제를 해결한다.

$$ \bar{D}_{\mathrm{KL}}^{\rho}\left(\theta_{1}, \theta_{2}\right):=\mathbb{E}_{s \sim \rho}\left[D_{\mathrm{KL}}\left(\pi_{\theta_{1}}(\cdot \mid s) | \pi_{\theta_{2}}(\cdot \mid s)\right)\right] $$

$\rho$는 discounted visitation frequency로 모든 상태가 아닌 방문했던 경로에서 sampling한 path를 따라가며 계산한 것으로 이는 충분히 계산이 가능하다. 이를 반영해서 다음의 최적화 문제로 바꿀 수 있다.

$$\tag{12} \begin{aligned} &\underset{\theta}{\operatorname{maximize}} L_{\theta_{\text {old }}}(\theta) \cr &\text { subject to } \bar{D}_{\mathrm{KL}}^{\rho_{{\theta}_\text { old }}}\left(\theta_{\text {old }}, \theta\right) \leq \delta \end{aligned} $$

이와 유사한 방식의 정책 update는 Section 7, 8에서 비교되며 heuristic이 들어가 찜찜한 부분은 실험적으로 성능을 비교했을 때 (11)을 사용한 것과 유사한 성능이 나왔음을 보이며 정당화된다.

Sample-Based Estimation of the Objective and Constraint

강화학습에서 sample-based estimation은 중요하다. 대부분의 경우 MDP를 모르는 상태에서 최적정책을 찾아야 하며 현실적으로 이를 달성하는 방법은 관측한 데이터를 사용하는 것이다. 이 때 관측한 데이터 기반으로, 즉 sample-based로 접근하려면 최적화하는 문제가 sample로 계산할 수 있는 형태여야 한다. 강화학습 알고리즘들에서 이를 달성하는 방식은 식에서 쉽게 찾을 수 있는데 바로 기대값 $\mathbb{E}$ operator를 사용하는 것이다. 가지고 있는 data를 사용해 추정하려다 보니 기대값을 활용하게 되며 이러한 방법을 Monte Carlo simulation이라고 한다. 간단히 말해 random sampling을 열심히 하면 원하는 수치를 근사시킬 수 있다는 것이다.

이제 (12)의 식을 $\mathbb{E}$로 표현하게 바꾸면 된다. 일단 (12)의 식을 (3)에 의해 전개하면 다음과 같이 된다.

$$\tag{13} \begin{aligned} \underset{\theta}{\operatorname{maximize}} & \sum_{s} \rho_{\theta_{\text {old }}}(s) \sum_{a} \pi_{\theta}(a \mid s) A_{\theta_{\text {old }}}(s, a) \cr &\text { subject to } \bar{D}_{\mathrm{KL}}^{\rho_{\text {old }}}\left(\theta_{\text {old }}, \theta\right) \leq \delta \end{aligned} $$

여기서 visitation frequency $\rho$부분인 $\sum_{s} \rho_{\theta_{\text{old}}}(s)[\cdots]$는 $\frac{1}{1 - \gamma} \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}}}[\cdots]$로 바꾸게 된다. 앞의 식은 각 상태별로 visitation frequency를 가중치처럼 취급해 합하는 과정이다. 바꾸게 되는 식은 초반부에 언급한 discounted visitation frequency의 정의식을 참고하면 이해하기가 쉬워진다. 정의를 보면 time step이 진행될 수록 discount를 적용하게 되는데 각 상태별로 visitation frequency를 더하는 것은 $\gamma$를 비율로 하는 등비무한급수의 합으로 계산할 수 있다.

그 다음으로는 advantage 값인 $A_{\theta_{\text{old}}}$를 $Q$-value로 바꾸는 것이다. Advantage는 행동가치에서 상태가치를 뺀 값으로 정의가 되는데 $a$에 대한 summation을 살펴보면 각각의 행동들에 대해 어차피 속해있는 상태 $s$는 같으므로 상수를 빼는 것과 같아 최적화문제의 해를 바꾸지 않는다. 상수만큼 뺐냐 빼지 않았냐의 차이일 뿐이다.

마지막으로 $\sum_{a}$부분은 importance sampling을 사용해준다. 이 때, $q$는 sampling distribution으로 old policy로 생각할 수 있으며 각 상태 $s_{n}$이 loss에 기여하는 정도로 아래와 같이 표현하게 된다.

$$ \sum_{a} \pi_{\theta}\left(a \mid s_{n}\right) A_{\theta_{\text {old }}}\left(s_{n}, a\right)=\mathbb{E}_{a \sim q}\left\lbrack\frac{\pi_{\theta}\left(a \mid s_{n}\right)}{q\left(a \mid s_{n}\right)} A_{\theta_{\text {old}}}\left(s_{n}, a\right)\right\rbrack $$

이를 모두 반영해주면 문제는 이제 아래와 같이 바뀐다.

$$ \begin{aligned} \underset{\theta}{\operatorname{maximize}} &\mathbb{E}_{s \sim \rho_{\theta_{\text {old}}}, a \sim q} \left[\frac{\pi_{\theta}(a \mid s)}{q(a \mid s)} Q_{\theta_{\text {old }}}(s, a)\right] \cr &\text { subject to } \mathbb{E}_{s \sim \rho_{\theta_{\text {old}}}}\left[D_{\mathrm{KL}}\left(\pi_{\theta_{\text {old }}}(\cdot \mid s) | \pi_{\theta}(\cdot \mid s)\right)\right] \leq \delta \end{aligned} $$

이제 목적함수와 제한조건이 모두 기대값 형태로 표현되어 sample-based 방식을 사용할 수 있게 되었다. 남은 과정은 data를 활용해서 위의 최적화 문제를 풀면 되는 것이다.

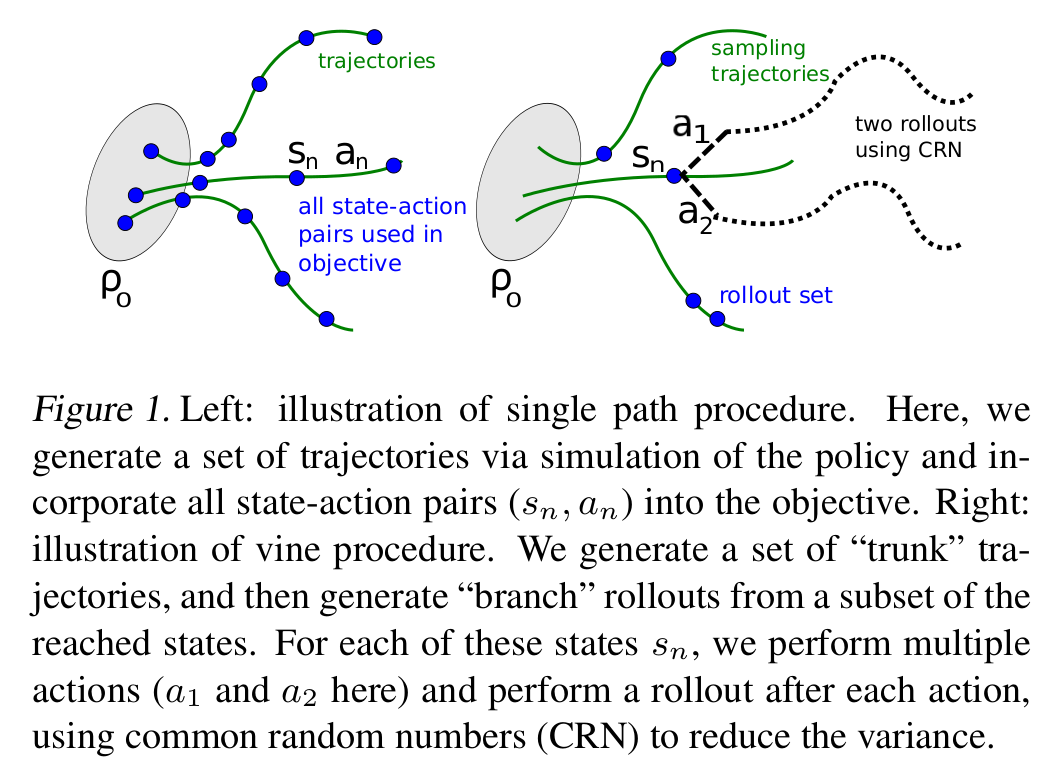
여기서 저자는 두가지 방식을 제시한다. 첫 번째 방식은 single path라는 방식으로 policy gradient estimation 방식으로 각각의 trajectory에서 sampling하는 방식이다. TRPO라고 하면 이 방식을 우선 생각하면 된다. 다른 방식은 vine이라는 방식인데 덩굴이라는 이름에서 보여지듯 single path와는 대비되는 방식으로 rollout set을 구성하여 각각의 상태에 대해서 여러가지 행동을 해보는 방식이다.

Single Path

Single path는 초기상태분포 $\rho_{0}$에서 초기상태 $s_{0}$를 sampling하고 이전 정책 $\pi_{\theta_{text{old}}}$에 따라 행동을 선택하며 일정 timestep을 진행해 trajectory를 만든다. 예를 들어 $T$개의 timestep만큼 simulation을 진행하면 $s_{0}, a_{0}, s_{1}, a_{1}, \ldots, s_{T-1}, a_{T-1}, s_{T}$의 trajectory를 얻게 된다. 이 떄 $q(a \mid s) = \pi_{\theta_{\text{old}}}$를 사용해서 (14)식에 넣어주면 된다. $Q_{\theta_{\text{old}}}(s, a)$는 각 상태에서 return을 계산해 대입하면 된다.

Vine

Vine은 single path처럼 $s_{0}$를 sampling하고 $\pi_{\theta_i}$를 사용해 trajectory를 만들어 낸다. Single path와 차이점은 single path는 하나의 trajectory를 만들어내지만 vine은 덩굴처럼 여러개의 trajectory를 만들게 된다. 이렇게 여러개의 trajectory를 만들고 trajectory들 중에서 $N$개의 상태에 대해 subset을 정하고 이를 $s_1, s_2, \ldots, s_N$라고 쓰며 roll-out set이라고 한다. 각각의 rollout set의 $s_n$에서 $K$번의 action을 sampling 할 수 있다. ($a_{n,k} \sim q(\cdot \mid s_{n})$) 이렇게 $s_{n}$에서 sampling 한 $a_{n,k}$에서 trajectory를 따라가며 $\hat{Q}_{\theta_i}(s_{n}, a_{n,k})$를 추정할 수 있다.

하나의 rollout-set에 대해서 $L_{\theta_{\text{old}}}$는 다음과 같이 계산할 수 있다.

$$\tag{15} L_{n}(\theta)=\sum_{k=1}^{K} \pi_{\theta}\left(a_{k} \mid s_{n}\right) \hat{Q}\left(s_{n}, a_{k}\right) $$

이 때 action space $\mathcal{A} = {a_1, a_2, \ldots, a_K}$이다. 이 식은 importance sampling을 사용해 surrogate objective를 추정하면 아래와 같이 표현된다. (self-normalized estimator 참고)

$$\tag{16} L_{n}(\theta)=\frac{\sum_{k=1}^{K} \frac{\pi_{\theta}\left(a_{n, k} \mid s_{n}\right)}{\pi_{\theta_{\text {old }}}\left(a_{n, k} \mid s_{n}\right)} \hat{Q}\left(s_{n}, a_{n, k}\right)}{\sum_{k=1}^{K} \frac{\pi_{\theta}\left(a_{n, k} \mid s_{n}\right)}{\pi_{\theta_{\text {old }}}\left(a_{n, k} \mid s_{n}\right)}} $$

$s_n$에 대해서 $K$개의 행동에 대해서 추정하였으므로 각각의 rollout set $s_n \sim \rho(\pi)$에 대해서 평균을 구하면 $L_{\theta_{\text{old}}}$에 대한 estimator를 얻을 수 있다.

Vine은 여러번의 simulation에 대한 평균이므로 분산이 줄어들 것을 기대할 수 있지만 연산량도 매우 커지게 됨을 예상해 볼 수 있다.

Practical Algorithm

이번 section에서 앞의 두 가지 single path와 vine을 기반으로 앞서 실용적으로 사용하기 어려웠던 문제를 해결한 알고리즘을 제시한다.

이 알고리즘은 다음의 과정을 반복해서 수행한다.

1. Single path나 vine을 사용해 $Q$-value에 대해서 Monte Carlo 추정을 하면서 state-action pair data를 모은다.
2. Sample 평균을 이용해 (14)를 계산한다.
3. (14)의 제한조건 최적화 문제를 풀어 $\theta$를 update한다. 이 떄, conjugate gradient algorithm을 사용한 뒤 line search를 사용해 policy parameter를 update한다.

3번은 간단하게 쓰여진 것에 반해서 실제로는 많은 단계를 포함한다. 세부적인 사항은 Appendix C에서 다루고 있는데 이 부분을 좀 더 살펴보자. (14)의 제한조건 최적화문제는 다음 문제를 푸는 것이다. $$ \operatorname{maximize} L(\theta) \text { subject to } \bar{D}_{\mathrm{KL}}\left(\theta_{\mathrm{old}}, \theta\right) \leq \delta $$ 이 과정에서 natural policy gradient의 내용이 사용된다. 즉 목적함수인 $L$은 1차근사를 하고 제한조건인 $D_{\mathrm{KL}}$에 대해서는 이차근사를 한다. 여기서는 natural policy gradient의 아이디어를 그대로 사용한다고 볼 수 있다. Fisher information matrix는 KL divergence의 두 분포에 대한 Hessian임이 알려져있다. 즉, Fisher information matrix는 그 자체로 KL divergence metric에 대해서 공간의 curvature를 정의한다. 따라서 이를 이용해 이차근사를 적용할 수 가 있는 것이다. 다만 natural policy gradient에서 방향과 step size가 계산이 가능하다고 하더라도 Fisher information matrix를 구하는 비용도 만만치 않고 natural policy gradient 연산에는 Fisher information matrix의 역함수가 포함되어 있다. 행렬의 크기와 역함수의 계산비용을 감안하면 이는 계산하기에 너무 비싼 연산이 되어버린다. 따라서 이 때 발생하는 연산량의 문제를 해결하기 위해서 저자는 conjugate gradient method를 도입하는 것이다. Conjugate gradient method를 통해서 search direction을 찾게 되고 그 다음으로 얼마만큼 이 gradient를 움직여 줄지를 결정해야한다. 이 과정에 필요한 연산은 conjugate gradient를 사용하면서 얻을 수 있으므로 충분히 계산이 가능하다.

이제 위의 3단계에서 언급된 line search가 어디서 사용되는지 알아보자. 위에서 step size를 구했지만 이 step size가 trust region에 들어간다는 보장이 없다. 지금까지 논의된 중요한 내용 중 하나는 $L$을 향상시키되 trust region안에 있도록 하는 것이다. 이를 식으로 나타내면 $L_{\theta_{\text {old }}}(\theta)-\mathcal{X}\left[\bar{D}_{\mathrm{KL}}\left(\theta_{\text {old }}, \theta\right) \leq \delta\right]$을 만족하는 것이고 이 때, $\mathcal{X}[\cdots]$는 안의 식이 true일 때 0으로 penalty를 주지 않으며 안의 식이 false일 때 $\infty$로 설정되어 무한대의 penalty를 주어 해당 상황이 일어나지 않게끔 한다. 따라서 앞서 구한 step size를 사용해서 trust region식을 만족하도록 줄여나가야 하는데 이 때 사용하는 것이 바로 line search인 것이다. 이 과정이 없게 되면 trust region내의 이동을 보장할 수 없게된다.

이제 전체 과정을 정리하면 다음과 같다.

• TRPO는 KL divergence에 대한 제한조건을 갖고 surrogate objective 함수를 최적화하는 문제로 바꾼다. 이 때 Lagrange multiplier처럼 최적화 식을 쓰면 문제가 발생한다. 식 (9)에서 $C$가 정의된 것을 살펴보자. $\gamma$는 reward discount로 보통 0.99같은 값을 쓰는데 이 값을 사용하게 되면 $C$는 분자에서 10000배를 키워주게 된다. 즉 $C$가 너무 커지다보니 penalty가 크게 들어가면서 각각의 step이 매우 작아지게 되는 것이다. 이러한 문제를 해결하기 위해서 TRPO에서는 아에 KL divergence 변화에 대해 hard constraint $\delta$를 사용함으로써 이러한 문제를 피한다.
• 식 (11)에서 (12)로 넘어가는 과정에서 저자가 heuristic을 적용하였다고 언급한 것처럼 이론식을 그대로 지키려면 $D_{\textrm{KL}}^{\textrm{max}}$를 사용하는 것이 맞으나 수치계산에서 parameter set에 대해 최대 KL divergence계산을 하는 것은 어렵다. 따라서 평균으로 대체한다.
• Kakade & Langford(2002)에서는 advantage function에 대한 추정오차를 반영하지만 단순화를 위해서 TRPO에서는 advantage function의 추정오차는 무시하였다.

Connections with Prior Work

개인적으로 생각하기에 이 논문에서 가장 많은 이론적 토대를 두고 있는 것은 Kakade의 natural policyt gradient논문이다. (12)에서 유도된 식에 대해 목적함수를 일차근사, 제한조건을 이차근사한 것이 natural policy gradient이다. Natural gradient는 다음과 같이 표현된다. Fixed penalty coefficeint(Lagrange multiplier)가 사용되고 있음에 유의하자.

$$ \begin{aligned} \underset{\theta}{\operatorname{maximize}} &\left[\left.\nabla_{\theta} L_{\theta_{\text {old }}}(\theta)\right|_{\theta=\theta_{\text {old }}} \cdot\left(\theta-\theta_{\text {old }}\right)\right] \cr &\text { subject to } \frac{1}{2}\left(\theta_{\text {old }}-\theta\right)^{T} A\left(\theta_{\text {old }}\right)\left(\theta_{\text {old }}-\theta\right) \leq \delta \cr &\text { where } A\left(\theta_{\text {old }}\right)_{i j} = \left.\quad \frac{\partial}{\partial \theta_{i}} \frac{\partial}{\partial \theta_{j}} \mathbb{E}_{s \sim \rho_{\pi}}\left[D_{\mathrm{KL}}\left(\pi\left(\cdot \mid s, \theta_{\text {old }}\right) | \pi(\cdot \mid s, \theta)\right)\right]\right|_{\theta=\theta_{\text {old }}} \end{aligned} $$

이 때, $\theta_{\text {new }}=\theta_{\text {old }}+\left.\frac{1}{\lambda} A\left(\theta_{\text {old }}\right)^{-1} \nabla_{\theta} L(\theta)\right|_{\theta=\theta_{\text {old }}}$의 step size에 해당하는 $\frac{1}{\lambda}$는 algorithm parameter로 주어져야 한다. TRPO는 이 부분을 각각의 학습 step에서 조절하도록 하였다는데 차이가 있다. 논문에서도 언급하듯, 얼핏 보면 step size 조절방법만 바꾸어준게 그리 대단하나 싶지만 실제로 이 방식을 개선함으로써 큰 문제들에 대해서도 작동하게 할 수 있을만큼 알고리즘 성능의 유의한 차이를 가져왔다고 언급한다.

Experiments

논문에서는 실험을 통해 다음의 질문에 답하고자 하였다.

1. Single path와 vine의 성능은 어떤 특징을 갖는가?
2. TRPO는 이전 방식들에 비해 성능 측면에서 어떤 차이를 갖는가?
3. TRPO는 large-scale 문제로 확장될 수 있는 방법인가? 다른 방식들과 최종 성능, 시간, sample complexity측면에서 어떤 차이를 갖는가?

질문 1., 2.를 위해서 TRPO의 single path, vine 각각에 대한 TRPO와 다른 policy optimization algorithm에 대한 성능비교를 하는 실험과 (3)을 확인하기 위해 Atari game을 비롯한 환경에서 비교를 하였다.

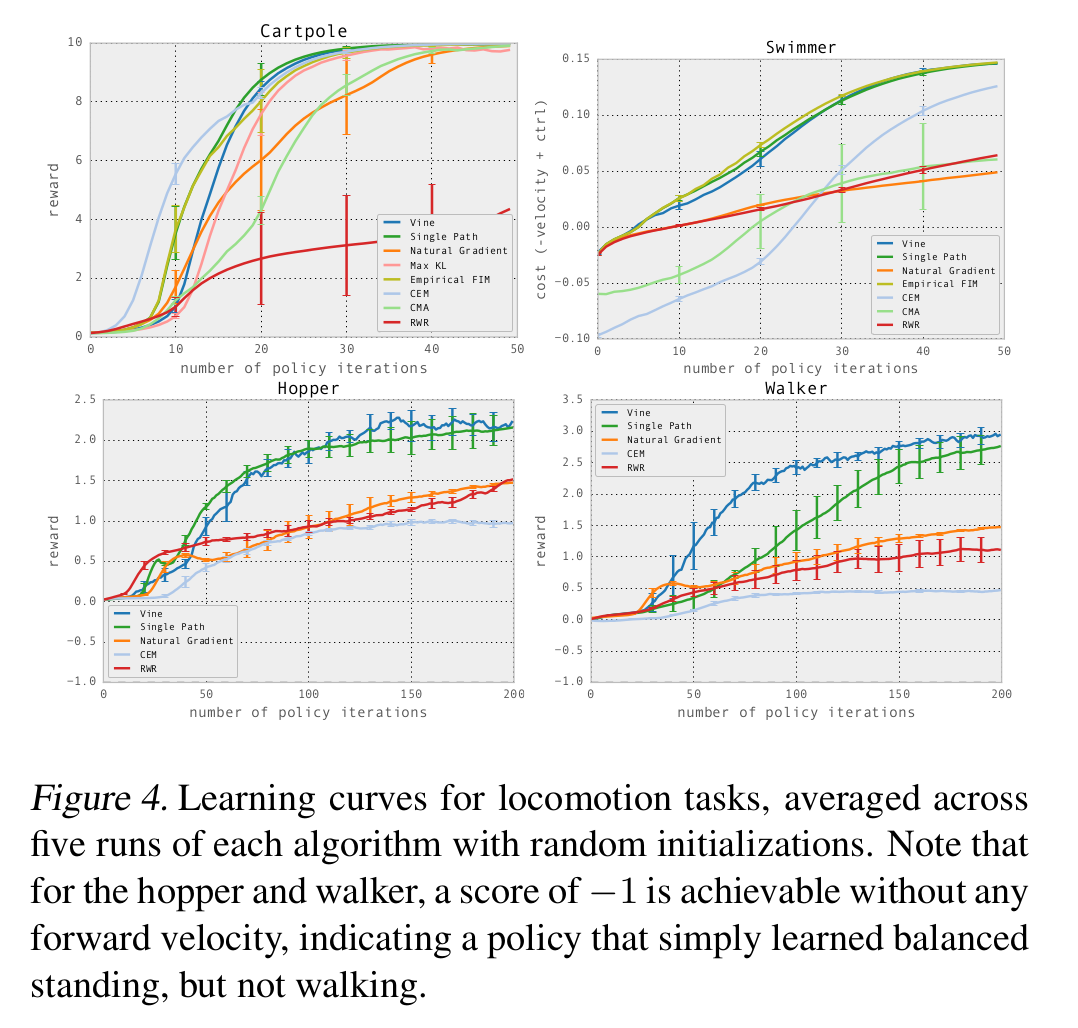
다음은 MuJoCo simulator의 Swimmer, Hoppper, Walker 환경의 결과이다. single path와 vine 모두 다른 알고리즘 대비 좋은 성능을 보여주고 있다.

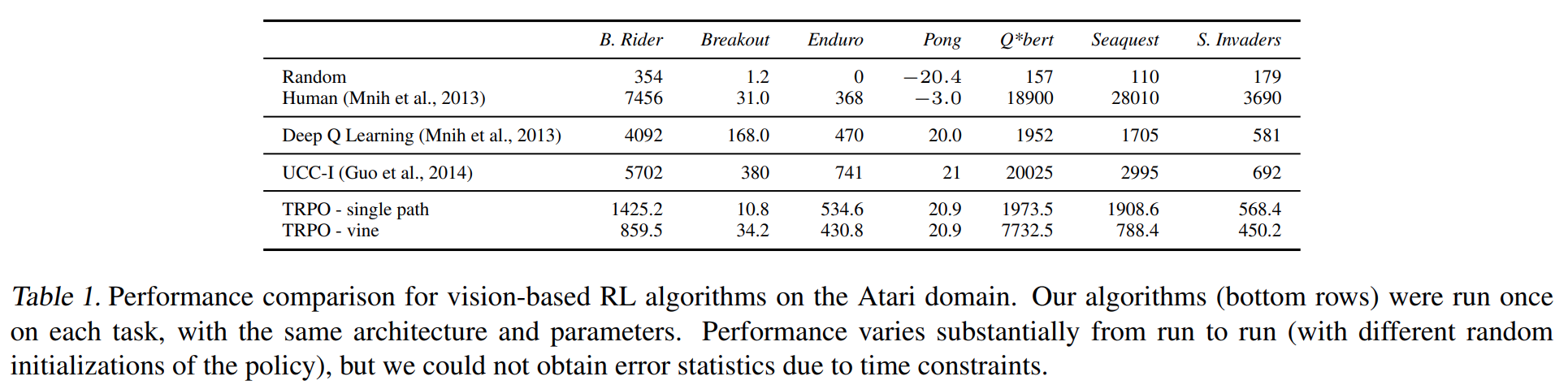
다음은 Atari게임 중 일부 게임들에 대한 성능 비교이다. TRPO가 DQN에 비해서도 성능이 크게 개선되지 않고 일부 게임에서는 현저히 떨어지는 성능을 보이는 것을 볼 수 있다. 하지만 TRPO는 다른 알고리즘보다 더 범용적으로 사용될 수 있는 알고리즘으로써 이 정도의 성능을 만들었다는 의의가 있다. 일례로 DQN은 action space가 연속공간일 경우에는 적용할 수가 없다.

Discussion

TRPO논문은 이론적으로는 expected return에 대한 local approximation에 대해서 KL divergence 제한조건을 반영해 개선이 보장되는 이론을 만들었다는데 의의가 있다. 사용되는 수학이론이 꽤나 깊은 편으로 이 자체로 의미있는 contribution이며 이와 더불어 실용적으로 사용할 수 있는 알고리즘까지 제시하고 policy learning task의 실험결과들을 통해 학습을 할 수 있음을 보였다. 논문에서 언급하는 것처럼 scalable하고 증명된 튼튼한 이론적 토대를 가진 알고리즘이다. 다만, 다양한 문제에 적용하기위해서는 계산비용이 상당하다는 단점을 갖고 있다. 이를 개선한 PPO가 발표되는데 PPO는 TRPO의 배경을 이해하고 있다면 쉽게 읽을 수 있는 논문이다.

Bibliography

Schulman, John, et al. “Trust region policy optimization.” International conference on machine learning. PMLR, 2015.