4.5 Singular Vector Decomposition

Singular Vector Decomposition (SVD)는 보통 선형대수학 수업교재의 후반부에 나온다. 앞서 다룬 Eigendecomposition의 일반화된 형태일뿐만 아니라 선형대수학의 기본적인 개념을 종합해서 사용하기 때문일 것이다.

학부과정에서 선형대수학을 수강할 때 Gilbert Strang의 교재를 사용했었다. Strang은 SVD에 대해 다음과 같이 언급한다.

“Fundamenetal theorem of linear algebra”

실제로 SVD는 모든 행렬에 대해 적용가능하고 항상 존재한다는 강력한 성질을 가지지만 이런 성질과 더불어 fundamental theorem이라고 할 만큼 많은 의미를 함의하기 떄문에 저렇게 말씀하신게 아닐까 싶다. 여기서는 SVD에 대해 다룬다.

Singular Value Decomposition

앞서 다루었던 분해는 대부분 $n \times n$ 크기의 행렬에 한정해서 적용할 수 있었다. 이와는 다르게 SVD는 일반적인 행렬 모두에 대해 적용가능한 개념이다. 심지어 역행렬 $\boldsymbol{P}^{-1}$가 존재해야 할 수 있다는 등의 조건도 없다. 항상 가능하다. 뿐만 아니라, Linear mapping $\Phi: V \rightarrow W$을 표현하는 $\boldsymbol{A}$가 기하학적 관점에서 두 벡터공간을 어떻게 변환하는지를 단계적으로 보여준다. SVD에 대해서 알아보자.

$\boldsymbol{\Sigma}$의 대각성분인 $\sigma_{i}, i = 1, \ldots, r$를 singular values라고 한다. 그리고 이 singular values는 첫 번째 행부터 순차적으로 작아지는 내림차순으로 정렬되어있어야 한다. 따라서 $\sigma_{1}, \geqslant, \sigma_{2}, \geqslant \cdots, \geqslant \sigma_{r} \geqslant 0$이다. 그리고 $\boldsymbol{u}_{i}$는 left-singular vectors라고 하며 $\boldsymbol{v}_{j}$는 right-singular vectors라고 한다.

이제 분해된 각각의 행렬을 살펴보자. 우선 $\boldsymbol{\Sigma}$을 singular value matrix라고 하며, singular value matrix는 SVD를 할 때 유일하다. Singular value matrix는 행렬 $\boldsymbol{A}$와 같은 크기인 $\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}$이다. 따라서 singular value matrix는 singular value와 zero-padding으로 구성된 형태이다. 많은 경우 데이터는 행의 개수 $m$이 열의 개수 $n$보다 큰 경우가 대부분이다. $m > n$일 때 singular value는 $n$번째 행까지 채워지며 그 밑으로는 $\boldsymbol{0}^{\top}$으로 채워진다. 따라서 다음과 같은 형태를 갖게 된다.

$$ \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{1} & 0 & 0 \cr 0 & \ddots & 0 \cr 0 & 0 & \sigma_{n} \cr 0 & \cdots & 0 \cr \vdots & \ddots & \vdots \cr 0 & \cdots & 0 \end{bmatrix} $$

반대로 $m < n$이라면 $m$번째 열까지 Singular value가 채워지고 그 오른쪽으로 $\boldsymbol{0}$벡터들이 채워지게 된다.

$$ \boldsymbol{\Sigma} = \begin{bmatrix} \sigma_{1} & 0 & 0 & 0 & \cdots & 0\cr 0 & \ddots & 0 & 0 & \ddots & 0 \cr 0 & 0 & \sigma_{m} & 0 & \cdots & 0 \end{bmatrix} $$

Eigendecomposition의 식과 SVD의 식을 비교해보면, symmetric, positive definite 행렬에 대한 SVD가 eigendecomposition임을 알 수 있다. 즉 eigendecomposition은 SVD의 특수한 경우이다.

Geometric Intuitions for the SVD

Eigendecomposition에서와 비슷하게 SVD는 linear transformation matrix $\boldsymbol{A}$가 순차적으로 어떻게 변환하는지에 대한 기하학적 설명을 제공한다. 각 행렬의 형태는 다르지만 eigendecomposition이 $\boldsymbol{PD} \boldsymbol{P}^{-1}$이라는 순차적인 선형변환으로 해석했듯, SVD도 $\boldsymbol{U \Sigma}\boldsymbol{V}^{\top}$의 순차적인 변환으로 해석한다.

간략하게 정리하면 SVD는 일반행렬 $\boldsymbol{A} \in \mathbb{R}^{m \times n}$을 $n$차원 공간에서 $m$차원으로의 변환에 대해 다음과 같은 세가지 단계를 거치게 된다.

1. $\boldsymbol{V}^{\top}$에 의해 Basis를 변환한다.
2. $\boldsymbol{\Sigma}$에 의해 Basis를 Scaling하고 $n$차원에서 $m$차원으로 차원을 바꾸게 된다.
3. $\boldsymbol{U}$에 의해 Basis를 변환한다.

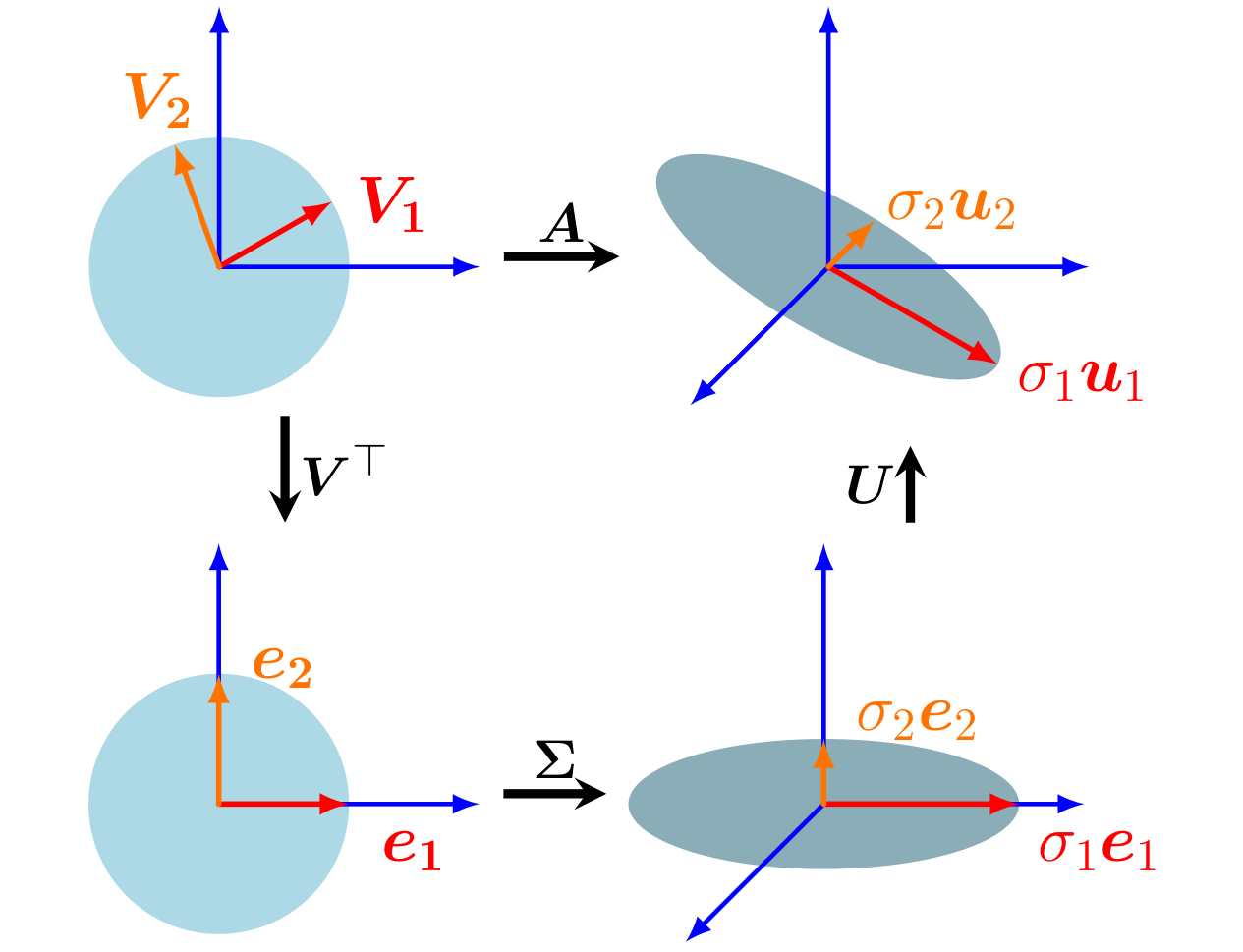
이제 각 단계에서 일어나는 일들을 세부적으로 알아보자. 결과적으로 우리는 선형변환 $\Phi: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$을 설명하고자 하며, $\mathbb{R}^{n}$과 $\mathbb{R}^{m}$을 구성하는 standard bases $B$와 $C$가 각각 있다고 하자. 그리고 각각의 변환된 basis는 $\tilde{B}, \tilde{C}$로 표기한다.

1. 행렬 $\boldsymbol{V}$는 basis $\tilde{B}$를 Standard Basis $B$로 변환해 준다. SVD에서 사용하는 것은 $\boldsymbol{V}^{\top} = \boldsymbol{V}^{-1}$(Orthogonal하니깐 Transpose가 Inverse이다)이므로 반대 방향, 즉 $B$에서 $\tilde{B}$의 basis로 바꾸어준다. 따라서 변환하는 벡터 $\boldsymbol{x}$는 $\tilde{B}$의 basis로 표현된다. 위 그림에서 살펴보면, 왼쪽 상단의 벡터 공간은 붉은색과 오렌지색의 basis를 사용한다. 여기에 $\boldsymbol{V}^{\top}$변환을 거치면서 왼쪽하단의 기본단위벡터로 표현하는 공간으로 변환된다.
2. $\boldsymbol{\Sigma}$ 변환을 함으로써 앞의 과정을 통해 얻은 $\tilde{B}$의 좌표계에서 $\boldsymbol{\Sigma}$는 해당성분을 $\sigma$만큼 Scaling 하고 차원을 더하거나 제거하게된다. 이 결과는 $\tilde{C}$에 표현된다. 왼쪽하단에서 오른쪽하단으로의 변환을 보면 붉은색과 오렌지색은 각각 Scaling되었고 없었던 차원이 추가된 것을 볼 수 있다.
3. $\boldsymbol{U}$는 $\mathbb{R}^{m}$차원에서의 Basis 변환으로 $\tilde{C} \rightarrow C$로 변환시킨다. 오른쪽하단에서 오른쪽상단으로의 그림은 차원은 유지하되 Basis가 다르게 표현되고 있는 것을 나타내고 있다.

SVD와 eigendecomposition의 가장 두드러지는 차이는 codomain에서의 basis이다. Eigendecomposition은 같은 벡터공간내에서 일련의 선형변환을 거쳐 최종적으로 기존의 basis로 표현되는 공간으로 돌아오지만, SVD는 domain과 codomain에서 basis가 모두 변경된다. 그도 그럴 것이 도착하는 차원부터가 다르다. 그리고 SVD에서 $\boldsymbol{\Sigma}$에 의해 이러한 차원간 basis변환이 정의된다.

Example Problem

교재 4.12의 예제문제를 Figure 4.9를 보며 이해해보자.

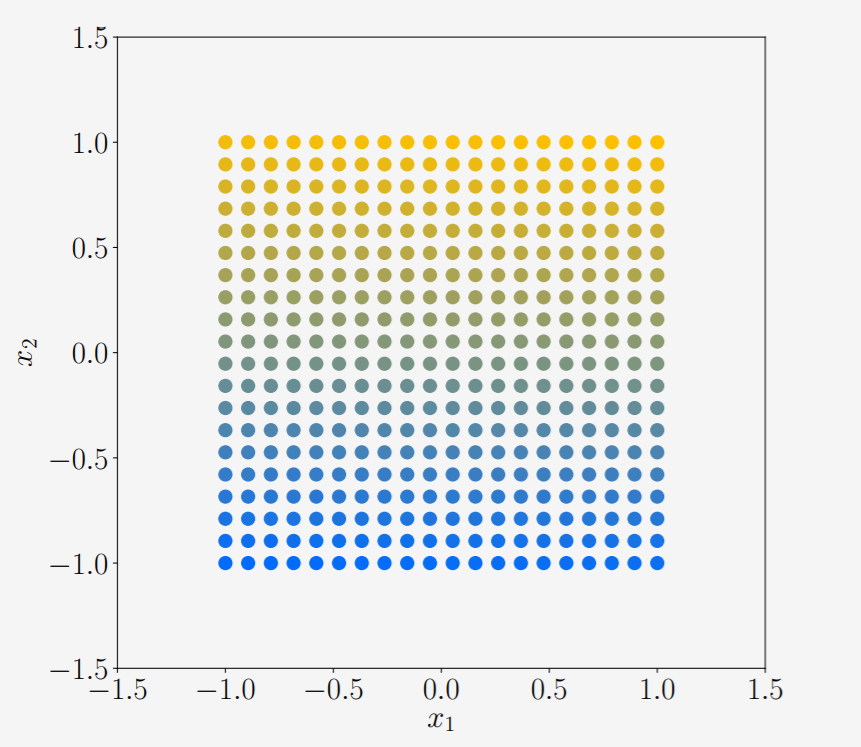
변환 $\boldsymbol{A}$는 2차원 벡터 $\mathcal{X} \in \mathbb{R}^{2}$를 3차원으로 변환하는 행렬이다. 변환하고자 하는 2차원 벡터공간은 $x, y$가 각각 -1.0 ~ 1.0의 값을 가지고 있는 사각형 공간으로 다음과 같다.

행렬 변환을 SVD로 나타내고 의미를 해석해보자.

$$ \begin{aligned} \boldsymbol{A} &= \begin{bmatrix} 1 & -0.8 \cr 0 & 1 \cr 1 & 0 \end{bmatrix} \cr &= \boldsymbol{U\Sigma} \boldsymbol{V}^{\top} \cr &= \begin{bmatrix} -0.79 & 0 & -0.62 \cr 0.38 & -0.78 & -0.49 \cr -0.48 & -0.62 & 0.62 \end{bmatrix} \begin{bmatrix} 1.62 & 0 \cr 0 & 1.0 \cr 0 & 0 \end{bmatrix} \begin{bmatrix} -0.78 & 0.62 \cr -0.62 & -0.78 \end{bmatrix} \end{aligned} $$

1. $\boldsymbol{V}^{\top}$이 곱해지면 다음의 연산을 통해 각 점들은 새로운 위치로 이동하게 된다. $$\boldsymbol{V}^{\top}\boldsymbol{x} = \begin{bmatrix} -0.78 & 0.62 \cr -0.62 & -0.78 \end{bmatrix} \begin{bmatrix} x_{1} \cr x_{2} \end{bmatrix}$$ 결과적으로 위의 변환은 $\mathcal{X}$를 회전시키게된다. 차원은 여전히 2차원임에 유의하자.

   

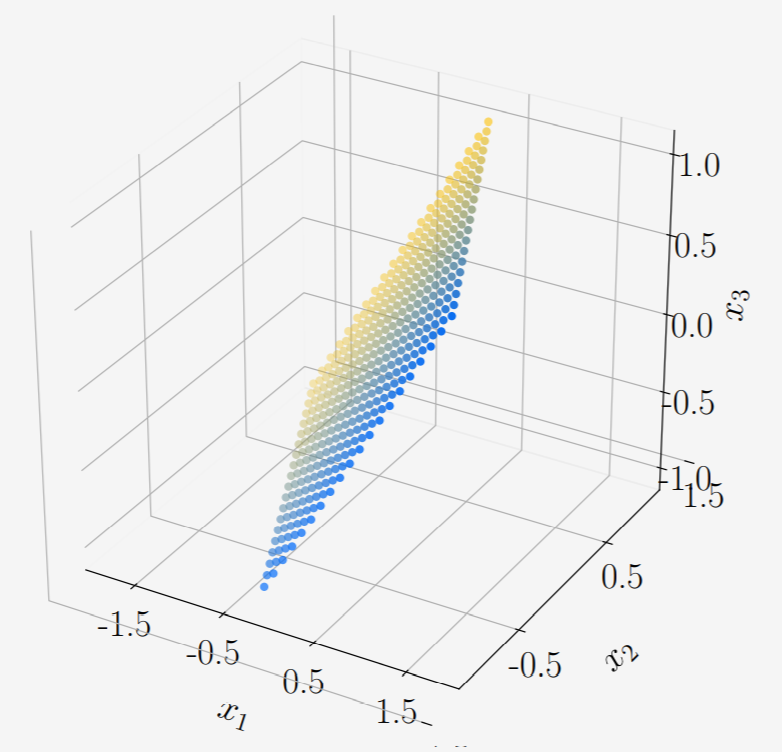
2. Singular value matrix $\boldsymbol{\Sigma}$는 위에서 변환된 Basis방향으로 각각 1.62배, 1.0배를 해주고 새로운 차원을 추가해준다. 밑에 그림을 보면 한쪽방향으로 1.62배만큼 늘어난 사각형으로 변해있고 3차원 공간에 표현된 것을 볼 수 있다. 눈여겨볼점은 차원이 추가가 되었을 뿐 성분 자체는 0이었으므로 $x_{3}$방향의 성분은 모두 0이다.

   

3. 마지막으로 변환 $\boldsymbol{U}$에 의해 최종 목적지인 $\boldsymbol{A}$의 codomain $\mathbb{R}^{3}$공간으로 변환시키게 된다. $\boldsymbol{U}$는 Singular value matrix에 의한 변환을 같은 차원내에서 basis change를 하는 역할이다. 이 변환에서는 모든 방향성분이 존재하는 행렬이므로 $x_{3}$도 값을 가질 수 있다.

   

Construction of the SVD

여기서는 어떻게 SVD가 항상 존재할 수 있고, 또 어떻게 계산하는지를 다룬다.

행렬 $\boldsymbol{A} \in \mathbb{R}^{m \times n}$의 SVD를 구하는 것은 codomain $\mathbb{R}^{m}$과 domain $\mathbb{R}^{n}$에 대해 $U = (\boldsymbol{u}_{1}, \ldots, \boldsymbol{u}_{m})$과 $V = (\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{n})$인 orthonormal bases를 찾는 것과 같다. 이 두 집합의 basis를 통해 $\boldsymbol{U}, \boldsymbol{V}$를 만들면 된다.

SVD를 구하는 과정은 다음의 순서대로 하면 된다.

1. Right-singular vector의 orthonormal set인 $\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{n} \in \mathbb{R}^{n}$을 찾는다. Spectral theorem에 의해 symmetric 행렬은 orthonormal basis인 eigenvector를 가지며 대각화가 가능하다. 임의의 행렬 $\boldsymbol{A} \in \mathbb{R}^{m \times n}$에 대해 $\boldsymbol{A}^{\top} \boldsymbol{A}$은 항상 symmetric하고 positive semidefinite하므로 $\boldsymbol{A}^{\top} \boldsymbol{A}$은 대각화가 가능하다. $$ \begin{aligned} \boldsymbol{A}^{\top} \boldsymbol{A} &= \boldsymbol{PD} \boldsymbol{P}^{\top} \cr &= \boldsymbol{P} \begin{bmatrix} \lambda_{1} & \cdots & 0 \cr \vdots & \ddots & \vdots \cr 0 & \cdots & \lambda_{n} \end{bmatrix} \boldsymbol{P}^{\top} \end{aligned} $$ $\boldsymbol{P}$는 직교행렬이며 orthonormal eigenbasis로 구성된다. 따라서 $\lambda_{i} \geqslant 0$은 $\boldsymbol{A}^{\top} \boldsymbol{A}$의 eigenvalue이다. 그런데 여기서 대각화와 right-singular vectors를 구하는게 무슨 상관이 있을까? SVD는 $\boldsymbol{A} = \boldsymbol{U \Sigma} \boldsymbol{V}^{\top}$이므로 이를 그대로 $\boldsymbol{A}^{\top} \boldsymbol{A}$에 대입하면, $$ \begin{aligned} \boldsymbol{A}^{\top} \boldsymbol{A} &= ( \boldsymbol{U \Sigma} \boldsymbol{V}^{\top} )^{\top} ( \boldsymbol{U \Sigma} \boldsymbol{V}^{\top} ) \cr &= \boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} \end{aligned} $$ 이 때, $\boldsymbol{U}, \boldsymbol{V}$는 orthogonal matrix이므로 $ \boldsymbol{U}^{\top} \boldsymbol{U} = \boldsymbol{I} $이다. 따라서 다음이 성립한다. $$ \begin{aligned} \boldsymbol{A}^{\top} \boldsymbol{A} &= \boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} \cr &=\boldsymbol{V} \begin{bmatrix}\sigma_{1}^{2} & 0 & 0 \cr 0 & \ddots & 0 \cr 0 & 0 & \sigma_{n}^{2} \end{bmatrix} \boldsymbol{V}^{\top} \end{aligned} $$ 앞서 얻은 결과와 대응시켜보면 다음의 관계가 성립한다. $$ \begin{aligned} \boldsymbol{V}^{\top} &= \boldsymbol{P}^{\top} \cr \sigma_{i}^2 &= \lambda_{i} \end{aligned} $$ 따라서, $\boldsymbol{A}^{\top} \boldsymbol{A}$의 eigenvector가 구성하는 $\boldsymbol{P}$는 $\boldsymbol{A}$에 대한 SVD의 right-singular vector가 구성하는 $\boldsymbol{V}$와 같다. 또한 $\boldsymbol{A}^{\top} \boldsymbol{A}$의 Eigenvalue는 $\boldsymbol{\Sigma}$의 Singular value 제곱값이다.

2. Left-singular vector의 orthonormal set인 $\boldsymbol{u}_{1}, \ldots, \boldsymbol{u}_{m} \in \mathbb{R}^{m}$을 찾는다. 앞에서 한 과정을 $\boldsymbol{A} \boldsymbol{A}^{\top} \in \mathbb{R}^{m \times m}$에 대해 똑같이 적용해주면 된다. 같은 과정을 거치면 다음의 결과를 얻는다. $$ \begin{aligned} \boldsymbol{A} \boldsymbol{A}^{\top} &= ( \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} ) ( \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V} )^{\top} \cr &= \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} \boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top} \cr &= \boldsymbol{U} \begin{bmatrix}\sigma_{1}^{2} & 0 & 0 \cr 0 & \ddots & 0 \cr 0 & 0 & \sigma_{m}^{2} \end{bmatrix} \boldsymbol{U}^{\top} \end{aligned} $$ 같은 이유로 $\boldsymbol{A} \boldsymbol{A}^{\top}$의 orthonormal eigenvector는 $\boldsymbol{A}$에 대한 SVD의 left-singular vectors와 같고 $\boldsymbol{U}$를 구성한다. 그리고 이렇게 구해진 eigenvector는 SVD의 codomain에 대한 orthonormal basis set을 구성한다.

3. $\boldsymbol{A}$의 변환에 대해 $\boldsymbol{v}_{i}$의 orthogonality를 보존하면서 $\boldsymbol{u}, \boldsymbol{v}$를 연결하는 관계(singular values)를 찾는다. 앞의 과정을 통해 $\boldsymbol{U}, \boldsymbol{V}$를 구할 수 있으므로 남은 것은 $\boldsymbol{\Sigma}$뿐이다. Orthonormal set $V$에서 $U$로 연결하는 변환을 만드는 것이 목표이다. $\boldsymbol{A}$에 대해 $\boldsymbol{v}_{i}$의 image가 orthogonal함을 이용하면 이를 보일 수 있다.(Orthogonal matrix에 의해 벡터를 변환하면 각도는 보존된다) $\boldsymbol{V}$의 두 eigenvector $\boldsymbol{v}_i, \boldsymbol{v}_{j}, i \neq j$는 서로 직교하므로 inner product는 0이다. $$ \begin{aligned} ( \boldsymbol{A} \boldsymbol{v}_{i} )^{\top} ( \boldsymbol{A} \boldsymbol{v}_{j} ) &= \boldsymbol{v}_{i}^{\top} ( \boldsymbol{A}^{\top} \boldsymbol{A} ) \boldsymbol{v}_{j} \cr &= \boldsymbol{v}_{i}^{\top} (\lambda_{j} \boldsymbol{v}_{j} ) \cr &= \lambda_{j} \boldsymbol{v}_{i} \boldsymbol{v}_{j} \cr &= 0 \end{aligned} $$ $m \geqslant r$인 경우 $\mathbb{R}^{m}$의 $r$차원 subspace의 basis는 ${ \boldsymbol{A} \boldsymbol{v}_{1}, \ldots, \boldsymbol{A} \boldsymbol{v}_{r}}$가 된다. $\mathbb{R}^{m}$에서의 basis이므로 이들은 $\boldsymbol{U}$의 basis가 되며 다음과 같이 normalization을 함으로써 left-singular vector를 구할 수 있다. $$ \begin{aligned} \boldsymbol{u}_{i} :&= \frac{\boldsymbol{A} \boldsymbol{v}_{i}}{\Vert \boldsymbol{A} \boldsymbol{v}_{i} \rVert} \cr &= \frac{1}{\sqrt{\lambda_{i}}} \boldsymbol{A} \boldsymbol{v}_{i} \cr &= \frac{1}{\sigma_{i}} \boldsymbol{A} \boldsymbol{v}_{i} \end{aligned} $$ 따라서 $\boldsymbol{A}^{\top} \boldsymbol{A}$의 eigenvector, 즉 right-singular vectors $\boldsymbol{v}_{i}$를 얻으면 위에서 계산한 $\boldsymbol{A}$의 normalized image를 통해 left-singular vectors $\boldsymbol{u}_{i}$를 얻을 수 있다. 그리고 singular value matrix에 의해 이 둘은 연결된다. 위식을 이항하면 다음의 식을 얻을 수 있는데 이 식을 Singular value equation이라고 한다. $$\boldsymbol{A} \boldsymbol{v}_{i} = \sigma_{i} \boldsymbol{u}_{i}, i = 1, \ldots, r$$ 이 식은 eigenvalue equation과 상당히 닮아있는데 eigenvector에 해당하는 벡터부분이 다르다는 차이가 있다. 열이 행보다 많은 $(n > m)$ 경우, Singular value equation은 $i \leqslant m$까지만 성립하며 $i > m$인 $\boldsymbol{u}_{i}$에 대해서는 정보를 얻을 수 없다. 반대로 행이 열보다 많은 ($m > n$) 경우, Singular value equation은 $i \leqslant n$에 대해서만 성립한다. $i > n$인 $\boldsymbol{v}_{i}$는 $\boldsymbol{A} \boldsymbol{v}_{i} = \boldsymbol{0}$이 된다.

Singular value equation에서 $\boldsymbol{v}_{i}$를 붙여서 $\boldsymbol{V}$를 만들고 $\boldsymbol{u}_{i}$를 붙여서 $\boldsymbol{U}$를 만들면 다음과 같이 쓸 수 있다. $$\boldsymbol{AV} = \boldsymbol{U \Sigma}$$ $\boldsymbol{A}$에 대해서 정리하면 $\boldsymbol{A}$의 SVD인 $\boldsymbol{A} = \boldsymbol{U \Sigma}\boldsymbol{V}^{\top}$이 구해진다.

Example Problem

다음 행렬의 SVD를 찾아보자.

$$ \boldsymbol{A} = \begin{bmatrix} 1 & 0 & 1 \cr -2 & 1 & 0 \end{bmatrix} $$

Step 1: Right-singular vectors as the eigen basis of $\boldsymbol{A}^{\top} \boldsymbol{A}$

앞에서 살펴본 바와 같이 Right-singular vector를 구하기 위해서는 $\boldsymbol{A}^{\top} \boldsymbol{A}$에 대해 Eigendecomposition을 하면 된다. $$ \begin{aligned} \boldsymbol{A}^{\top} \boldsymbol{A} &= \begin{bmatrix} 1 & -2 \cr 0 & 1 \cr 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 1 \cr -2 1 & 0 \end{bmatrix} \cr &= \begin{bmatrix} 5 & -2 & 1 \cr -2 & 1 & 0 \cr 1 & 0 & 1 \end{bmatrix}\end{aligned} $$ 이 행렬에 대해 Eigendecomposition을 적용하면 다음과 같다. $$ \begin{aligned} \boldsymbol{A}^{\top} \boldsymbol{A} &= \begin{bmatrix} \frac{5}{\sqrt{30}} & 0 & \frac{-1}{\sqrt{6}} \cr \frac{-2}{\sqrt{30}} & \frac{1}{\sqrt{5}} & \frac{-2}{\sqrt{6}} \cr \frac{1}{\sqrt{30}} & \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{6}} \end{bmatrix} \begin{bmatrix} 6 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{5}{\sqrt{30}} & \frac{-2}{\sqrt{30}} & \frac{1}{\sqrt{30}} \cr 0 & \frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \cr \frac{-1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \end{bmatrix} \cr &= \boldsymbol{PD}\boldsymbol{P}^{\top}\end{aligned} $$ $\boldsymbol{V}$는 SVD에서 right singular vectors $\boldsymbol{V}$이므로, $$ \boldsymbol{V} = \boldsymbol{P} = \begin{bmatrix} \frac{5}{\sqrt{30}} & 0 & \frac{-1}{\sqrt{6}} \cr \frac{-2}{\sqrt{30}} & \frac{1}{\sqrt{5}} & \frac{-2}{\sqrt{6}} \cr \frac{1}{\sqrt{30}} & \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{6}} \end{bmatrix} $$

Step 2: Singular-value matrix

Singular values는 $\boldsymbol{A}^{\top} \boldsymbol{A}$의 Eigenvalues의 square root이므로 쉽게 구할 수 있다. 또한 $\operatorname{rank}(\boldsymbol{A}) = 2$이므로 두 개의 Non-zero singular values $\sigma_{1} = \sqrt{6}, \sigma_{2} = 1$가 존재한다. $$ \boldsymbol{\Sigma} = \begin{bmatrix} \sqrt{6} & 0 & 0 \cr 0 & 1 & 0 \end{bmatrix} $$

Step 3: Left-singular vectors as the normalized image of the right-singular vectors

위의 공식에 대입하면 다음과 같이 $\boldsymbol{u}_{i}$를 얻을 수 있다. $$ \begin{aligned} \boldsymbol{u}_{1} &= \frac{1}{\sigma_{1}} \boldsymbol{A} \boldsymbol{v_{1}} \cr &= \frac{1}{\sqrt{6}} \begin{bmatrix} 1 & 0 & 1 \cr -2 & 1 & 0 \end{bmatrix} \begin{bmatrix} \frac{5}{\sqrt{30}} \cr \frac{-2}{\sqrt{30}} \cr \frac{1}{\sqrt{30}} \end{bmatrix} \cr &= \begin{bmatrix} \frac{1}{\sqrt{5}} \cr \frac{-2}{\sqrt{5}} \end{bmatrix} \cr \boldsymbol{u}_{2} &= \frac{1}{\sigma_{2}} \boldsymbol{A} \boldsymbol{v_{2}} \cr &= \frac{1}{1} \begin{bmatrix} 1 & 0 & 1 \cr -2 & 1 & 0 \end{bmatrix} \begin{bmatrix} 0 \cr \frac{1}{\sqrt{5}} \cr \frac{2}{\sqrt{5}} \end{bmatrix} \cr &= \begin{bmatrix} \frac{2}{\sqrt{5}} \cr \frac{1}{\sqrt{5}} \end{bmatrix} \cr \boldsymbol{U} &= [ \boldsymbol{u}_{1}, \boldsymbol{u}_{2} ] = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 & 2 \cr -2 & 1 \end{bmatrix} \end{aligned} $$ 하지만 컴퓨터에서 계산할 때, SVD를 계산하기 위해 $\boldsymbol{A}^{\top} \boldsymbol{A}$를 사용하는 방식은 비효율적이어서 사용하지 않는다. 자세한 계산방법은 사용하는 LAPACK에 따라 다르다.

Eigenvalue Decomposition vs. Singular Value Decomposition

여기서는 eigendecomposition과 SVD를 비교한다.

• Eigendecomposition $$ \boldsymbol{A} = \boldsymbol{PD} \boldsymbol{P}^{-1} $$
• SVD $$ \boldsymbol{A} = \boldsymbol{U \Sigma} \boldsymbol{V}^{\top} $$
• SVD는 어떠한 크기의 행렬에도 적용이 가능한 반면 eigendecomposition은 정사각행렬 $\mathbb{R}^{n \times n}$형태이고 $\mathbb{R}^{n}$의 Basis, 즉 full rank인 행렬에만 적용이 가능하다.
• Eigendecomposition의 $\boldsymbol{P}$의 벡터는 orthogonal할 필요는 없다. 하지만 SVD의 $\boldsymbol{U}, \boldsymbol{V}$의 벡터는 orthonormal하며 벡터의 위치변경은 rotation에 해당한다.
• Eigendecomposition과 SVD 모두 다음의 단계를 거치며 변환된다.
  1. Change of basis in the domain
  2. Independent scaling of each new basis vector and mapping from domain to codomain
  3. Change of basis in the codomain 한편, SVD는 domain과 codomain이 다른 차원의 벡터공간을 가질 수 있다는 차이점이 있다.
• SVD에서 $\boldsymbol{U}, \boldsymbol{V}$는 서로 역행렬의 관계가 아닌 반면 eigendecomposition의 $\boldsymbol{P}, \boldsymbol{P}^{-1}$은 역행렬 관계에 있다.
• SVD의 singular value matrix $\boldsymbol{\Sigma}$는 모두 실수이고 음수가 아닌 값을 가진다. 이 성질은 eigendecompositino의 diagonal matrix에서 항상 성립하지는 않는다.
• Projection 관점에서 eigendecomposition과 SVD는 밀접하게 연관되어있다.
  • $\boldsymbol{A}$의 Left-singular vectors는 $\boldsymbol{A} \boldsymbol{A}^{\top}$의 eigenvector이다.
  • $\boldsymbol{A}$의 right-singular vectors는 $\boldsymbol{A}^{\top} \boldsymbol{A}$의 eigenvector이다.
  • $\boldsymbol{A}$의 0이 아닌 singular values는 $\boldsymbol{A} \boldsymbol{A}^{\top}$과 $\boldsymbol{A}^{\top} \boldsymbol{A}$의 0이아닌 eigenvalues의 square root값이다.
• Symmetric matrix $\boldsymbol{A} \in \mathbb{R}^{n \times n}$에 대해서 eigenvalue decomposition과 SVD는 같다. (Spectral Theorem)

SVD Application: Recommender system

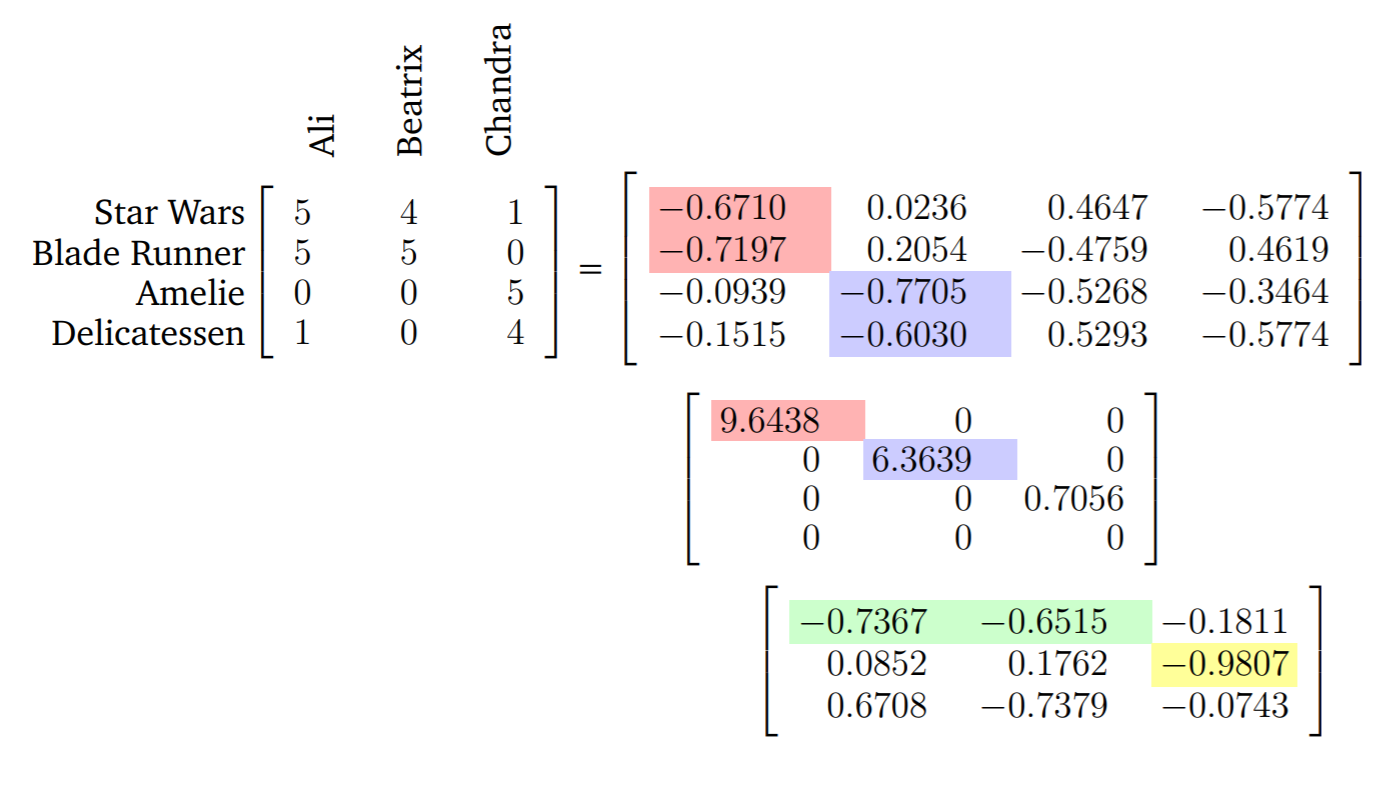
이번에는 SVD를 실생활의 문제에서 어떻게 활용할 수 있는지를 알아보자. 교재의 Example 4.14에 해당하는 문제이다. 세명의 사람 Ali, Beatrix, Chandra가 있고 이들이 네 편의 영화 Star Wars, Blade Runner, Amelie, Delicatessen에 대해 평가를 내렸다고 하자. 평가는 최악은 0, 최고는 5로 0~5의 스케일을 갖는다. 순서대로 영화를 행으로, 사람을 열로 놓고 각 값은 평가라고 할 때 다음과 같은 행렬을 만들 수 있다.

$$ \boldsymbol{A} = \begin{bmatrix} 5 & 4 & 1 \cr 5 & 5 & 0 \cr 0 & 0 & 5 \cr 1 & 0 & 4 \end{bmatrix} $$

SVD를 활용하면 사람들이 영화를 어떻게 평가를 했는지 그리고 어떤사람이 어떤 영화를 좋아하는지를 구조화해서 보여줄 수 있다. 특히, Left-singular vectors $\boldsymbol{u}_{i}$는 정형화된 영화간의 관계(stereotypical movies)를 $\boldsymbol{v}_{i}$는 정형화된 사람간의 관계(Stereotypical viewers)를 보여준다.

Left-singular vector $\boldsymbol{u}_{1}$를 보면, Star Wars, Blade Runner와 같은 Sci-Fi 장르에서 큰 값을 가지고 있음을 볼 수 있다. 따라서 $\boldsymbol{u}_{1}$은 Sci-Fi라는특정 장르를 가리키는 벡터로 추정할 수 있다. $\boldsymbol{v}_{1}$은 Ali와 Beatrix에게서 높은 값을 가리킨다. (Transpose 되어있음에 유의) 즉 $\boldsymbol{v}_{1}$는 Sci-Fi 장를 좋아하는 사람을 가리킨다고 의미를 부여할 수 있다.

$\boldsymbol{u}_{2}$는 Amelie, Delicatessen에 대해서 큰 값을 가지며 Sci-Fi장르와는 반대방향이고 거리도 멀게 나타난다. 즉 이 벡터는 French art house film theme이라는 의미를 부여할 수 있게된다. 위와 마찬가지로 $\boldsymbol{v}_{2}$는 Chandra와 같이 해당 장르를 좋아하는 사람으로 의미를 부여할 수 있을 것이다.

그리고 사람이 영화를 ‘어떻게’ 평가할 것인지에 대한 정보가 $\boldsymbol{\Sigma}$에 나타나게 된다. 예로, 극단적인 Sci-Fi 매니아라면 Sci-Fi 영화만 좋아하고 다른 장르에 대해서는 0점을 줄 것이다. 이와 같은 논리가 $\boldsymbol{\Sigma}$에 표현된다.

결과적으로, 특정 영화는 의미를 부여할 때 장르의 선형결합으로 분해되어 표현되고, 같은 방식으로 특정 사람은 영화장르 선호에 의한 선형결합으로써 분해되어 표현된다.

Reference

• Deisenroth, M. P., Faisal, A. A., & Ong, C. S. (2020). Mathematics for machine learning. Cambridge, United Kingdom: Cambridge University Press.