Skeleton-Aware Networks for Deep Motion Retargeting

Primal skeleton과 shared latent space를 도입해 다른 skeleton을 가지는 경우에도 motion retargeting을 할 수 있는 방법을 제안한다.

Abstract

논문에서는 다양한 skeleton을 공통의 skeleton으로 압축해 표현하는 방식을 제시하고 이렇게 압축된 skeleton을 primal skeleton이라고 한다. 이 primal skeleton을 만들기 위해 저자는 skeleton의 특징 중 하나인 계층적인 구조와 인접한 joint들의 정보를 압축하는 convolution, pooling, unpooling layer를 제시하고 이를 활용해 homeomorphic(이체동형) skeleton에 motion retargeting을 가능하게 하는 구조를 제시한다.

Introduction

이 논문에서는 retargeting 문제를 multimodal translation between unpaired domains로 정의한다. 전달하려는 motion이 학습데이터에 항상 있을 수는 없으므로 paired 되어있지 않은 데이터를 활용할 수 있어야하며 motion은 다 같은 동작이 아닌 고유의 modality를 가지므로 multimodal에 대한 학습이 이루어져야 할 것이다. 이 논문의 main contribution은 다음과 같다.

1. Skeleton의 정보를 인지하면서(skeleton-aware) 미분가능한 형태로 표현하는 motion processing framework을 제시한다. 간단하게 skeleton에 필요한 정보를 활용할 수 있는 convolution, pooling, unpooling layer를 제시하였다고 보면 된다.
2. 다른 skeleton에 적용 가능한 motion retargeting 방법론을 제시한다. 즉, motion을 만들어 낸 skeleton과 다른 joint 개수를 가지고 있는 skeleton에도 motion retargeting이 가능한 architecture를 제시하였다.

Related Work

IK에서부터 deep learning을 사용하는 motion retargeting 방법론의 변화와 특히 최근에 적용되는 convolutional layer의 활용, 시계열의 활용에 대한 연구들을 언급한다.

Overview

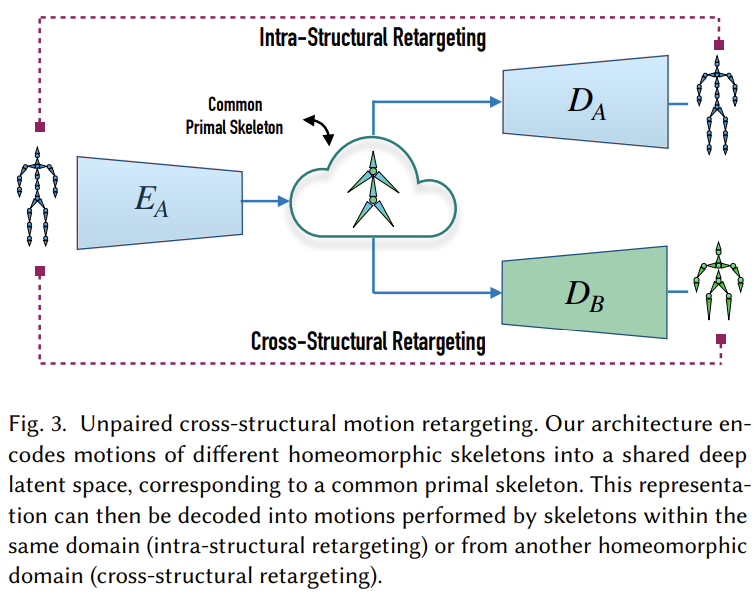
Main contribution에서 밝히는 것처럼 이 논문은 primal skeleton을 만드는 방식과 unpaired cross-structural motion retargeting을 목표로 한다.

Deep motion representation

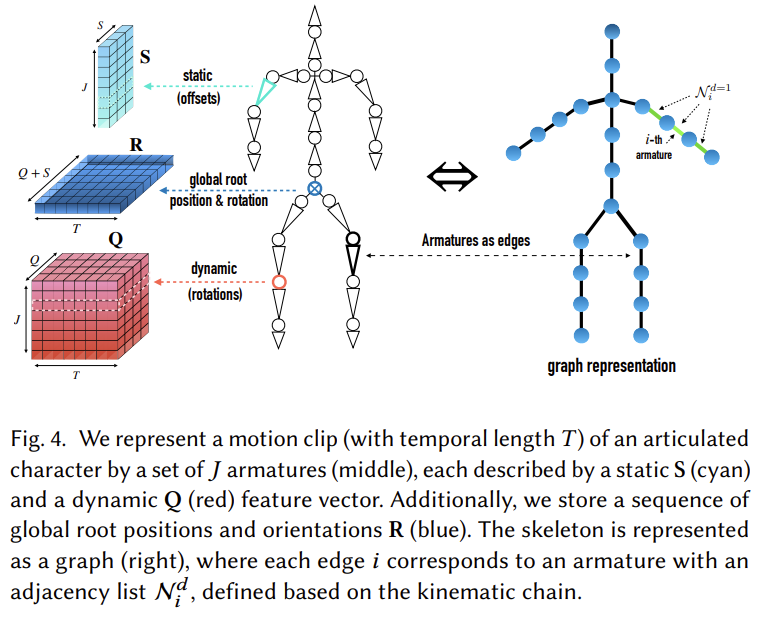
Motion sequence는 temporal set of armatures의 관점에서 본다. Aramature는 문맥상 link로 생각하여도 무리가 없다. 다시 말해, 일련의 움직임은 시간에 따른 link의 집합으로 보는 관점이다. 이 논문 전반에 걸쳐 offset정보를 static, time-independent 성질로 표현하고 회전정보는 dynamic, time-dependent로 표현한다. Offset은 3차원 벡터, 회전은 quaternion으로 표기한다. 이 둘을 통칭해 static-dynamic representation of motion feature라는 표현을 사용한다.

Deep Skeletal Operators

계속 언급되는 operator, 구체적으로는 convolution, pooling, unpooling에 대한 것으로 논문에서 말하는 skeleton-aware라는 성질은 이러한 operator/layer가 skeleton이 갖는 계층적인 구조와 다른 joint와의 인접성을 고려한다는 것을 의미한다.

Skeleton-aware Deep Motion Processing

Motion Representation

Motion representation은 특별한 차이 없이 보통 motion을 표현할 때 필요한 정보들을 이 논문에서도 똑같이 사용한다.

$T$는 motion sequence, $\boldsymbol{S} \in \mathbb{R}^{J \times S}$는 offset에 대한 정보로 static component라고 한다. $J$는 number of armature로 링크 개수라고 생가하면 된다. $\boldsymbol{Q} \in \mathbb{R}^{T \times J \times Q}$는 dynamic component로 회전량을 표현한다. Offset은 위치벡터이므로 $S=3$이고 회전량은 quaternion으로 표현하므로 $Q=4$이다.

Skeleton의 구조는 kinematic chain으로 표현되며 여기서 adjacency lists $\mathcal{N}^{d}$라는 개념을 도입한다. $\mathcal{N}^{d}$는 $i$번째 edge에서 거리가 $d$와 같거나 작은 edge의 집합을 의미한다.

이 내용들은 Figure 4에서 잘 표현된다.

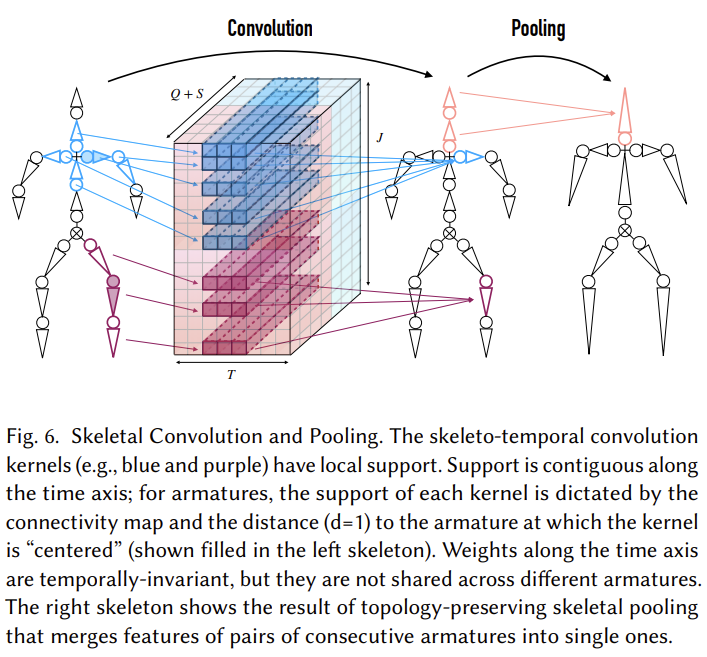
Skeletal Convolution

위의 convolution에서 시간축인 $T$로는 temporally-invariant한게 kernel이 적용되고 있음에 유의하자. 동시에 joint끼리는 독립적으로 처리된다. Static component인 offset은 tile & concatenation으로 붙어있는 구조이다.

저자는 여기서 skeleto-temporal convolution을 다음과 같이 적용하였다. 각각의 armature에 대해 적용된다.

$$\tag{1} \hat{\mathrm{Q}}_{i}=\frac{1}{\left|\mathcal{N}_{i}^{d}\right|} \sum_{j \in \mathcal{N}_{i}^{d}} \mathbf{M}_{j} * \mathbf{W}_{j}^{i}+\mathbf{b}_{j}^{i} $$

$\boldsymbol{M}_{j} \in \mathbb{R}^{T \times(Q + S)}$는 $j$번째 armature를 나타내고 $\boldsymbol{W}_{j}^{i} \in \mathbb{R}^{k \times (Q+S) \times K}$, $\boldsymbol{b}_{j}^{i} \in \mathbb{R}^{K}$에서 $k$ temporal support를, $K$는 learned filters를 의미한다. Convolution을 거치기 전후에 armature의 수는 보존된다. 여기서 말하는 support는 인접해있는 armature와의 connectivity map이라고 볼 수 있다.

Convolution을 거치게 되면 마치 image를 다룰 때 CNN이 그러하듯, 주변정보(여기서는 인접 aramature)의 정보를 압축해 갖고 있게 된다.

Topology Preserving Skeletal Pooling

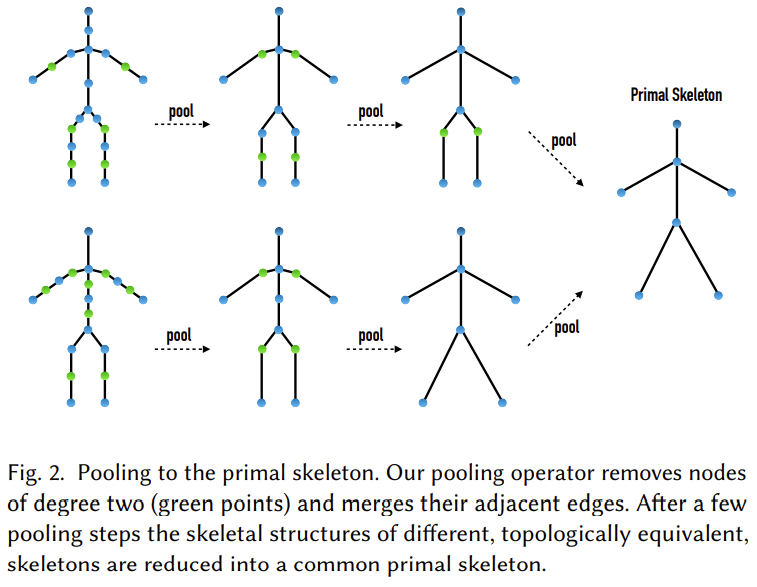
앞의 convolution은 차원을 줄이지 않는다. 하지만 primal skeleton을 만든다는 것은 다양한 skeleton들을 공통으로 사용할 수 있는 skeleton configuration으로 만들겠다는 것이므로 skeleton의 구조를 축소해주어야 한다. 즉 skeleton의 armature 개수를 조절해 주어야 한다는 뜻이고 이는 현재 skeleton에서 어떤 방식으로든 armature를 빼버린다는 말이 된다.

저자는 이러한 목적으로 pooling을 사용하며 저자가 제시한 방식은 node를 연결하는 edge의 degree가 2인 edge에 대해서 pooling을 적용한다. Figure 6의 오른쪽에 이러한 방식이 잘 도식화되어있다. Pooling 자체는 max pooling, average pooling이 모두 가능하다고 한다. Unpooling은 pooling의 반대과정으로 단순하게 feature ativation을 복사해서 늘려주는 것으로 learnable parameter를 포함하지 않는다. Pooling이후 original resolution으로 복구하기 위해서 사용된다.

Evaluation

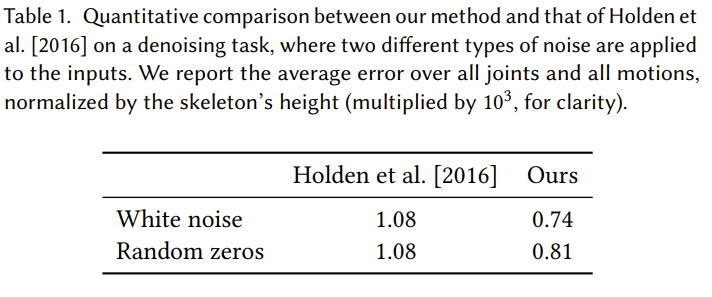
위에서 제시한 convolution이 skeletal-aware한 성질을 가지면서 convolution, pooling의 과정과 unpooling이 잘 되는지 확인하기 위한 목적으로 autoencoder를 사용해 검증한다. 2016년 Hodlen이 사용한 convolution, pooling과 비교가 이루어지며 autoencoder에 적용하였을 때 reconstruction에 대한 $l_{2}$ loss를 비교하면 더 낮은 loss를 갖는 것을 볼 수 있다.

Cross-structural Motion Retargeting

여기서는 앞에서 정의한 convolution, pooling, unpooling block을 활용하여 다른 skeleton에 대한 retargeting을 하는 방법을 다룬다.

Problem Setting

$\mathcal{M}_{A}, \mathcal_{B}$는 각각의 motion domain을 나타내며 skeletal structure는 $\mathcal{S}_{A}, \mathcal{S}_{B}$로 표기한다. 각각의 motion $i \in \mathcal{M}_{A}$는 $(\boldsymbol{S}_{A}, \boldsymbol{Q}_{A}^{i})$ pair로 표현한다. $\boldsymbol{S}_{A} \in \mathcal{S}_{A}$는 앞서 언급한대로 offset, $\boldsymbol{Q}_{A}^{i}$는 joint회전 정보이다.

다른 skeleton $\boldsymbol{S}_{B} \in \mathcal{S}_{B}$에 대해 현재 motion $(\boldsymbol{S}_{A}, \boldsymbol{Q}_{A}^{i})$이 가진정보를 $\tilde{\boldsymbol{Q}}_{B}^{i}$로 mapping하는 문제가 된다. 이는 다음과 같이 표현한다.

$$\tag{3} G^{A \rightarrow B}\left(\left(\mathrm{~S}_{A}, \mathrm{Q}_{A}^{i}\right) \in \mathcal{M}_{A}, \mathrm{~S}_{B} \in \mathcal{S}_{B}\right) \rightarrow\left(\mathrm{S}_{B}, \tilde{\mathrm{Q}}_{B}^{i}\right) $$

Network Architecture

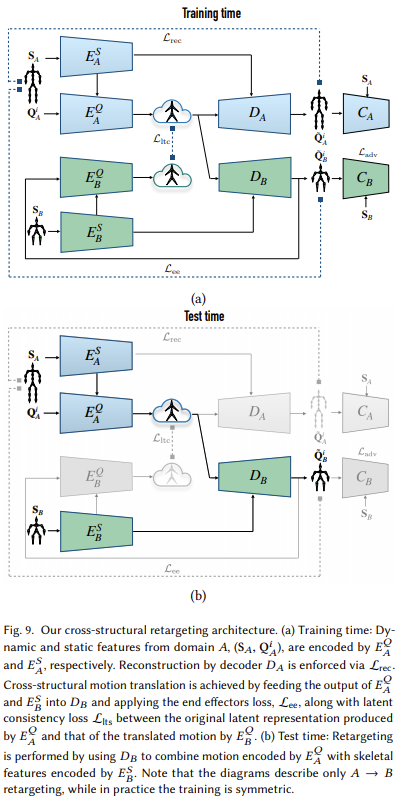
Network architecture는 위와 같다. Training time에서는 latent space를 훈련시켜야 하므로 당연하게 모든 block을 활용하며 test time에서는 본격적으로 다른 skeleton에 retargeting을 해야하므로 static component는 $B$에서 오지만 회전량과 관련된 정보는 latent space에서 제공받는 것을 볼 수 있다. 당연한 것이지만 구조를 볼 때 아무 skeleton으로 retargeting할 수 있는 것은 아닌 것을 파악할 수 있다. Training time에서 “사용할” skeleton 구조에 대한 latent consistency loss를 형성하므로 학습 때 아예 보지 못한 skeleton에 대해서는 정상적인 retargeting을 기대할 수 없다.

학습을 결정하는 loss는 다음과 같다.

• Reconstruction Loss

  Joint rotation과 joint position에 대한 오차를 계산한다.

  $$ \begin{aligned} \tag{4} \mathcal{L}_{\mathrm{rec}} &=\mathbb{E}_{\left(\mathrm{S}_{A}, \mathrm{Q}_{A}^{i}\right) \sim \mathcal{M}_{A}}\left[\left\lVert\left(D_{A}\left(\overline{\mathrm{Q}}_{A}^{i}, \overline{\mathrm{S}}_{A}\right), \mathrm{S}_{A}\right)-\mathrm{Q}_{A}^{i}\right\rVert^{2}\right] \end{aligned} $$ $$ \begin{aligned} \tag{5} &+\mathbb{E}_{\left(\mathrm{S}_{A}, \mathrm{Q}_{A}^{i}\right) \sim \mathcal{M}_{A}}\left[\left\lVert\mathrm{FK}\left(D_{A}\left(\overline{\mathrm{Q}}_{A}^{i}, \overline{\mathrm{S}}_{A}\right), \mathrm{S}_{A}\right)-\mathbf{P}_{A}^{i}\right\rVert^{2}\right] \end{aligned} $$

• Latent Consistency Loss

  Latent consistency loss는 shared representation에서 retargeted motion이 원본 clip과 동일한 dynamic feature를 갖도록 만들어준다.

  $$\tag{6} \mathcal{L}_{\mathrm{ltc}}=\mathbb{E}_{\left(\mathrm{S}_{A}, \mathrm{Q}_{A}^{i}\right) \sim \mathcal{M}_{A}}\left[\left\lVert E_{B}^{Q}\left(\tilde{\mathrm{Q}}_{B}^{i}, \overline{\mathrm{S}}_{B}\right)-E_{A}^{Q}\left(\mathrm{Q}_{A}^{i}, \overline{\mathrm{S}}_{A}\right)\right\rVert_{1}\right] $$

• Adversarial Loss

  Unpaired data를 사용하므로 discriminator로 하여금 실제 motion과 생성된 motion을 구별하도록 훈련시켜 보다 자연스러운 motion을 만들 수 있게 한다.

  $$\tag{7} \mathcal{L}_{\mathrm{adv}}=\mathbb{E}_{i \sim \mathcal{M}_{A}}\left[\left\lVert C_{B}\left(\tilde{\mathrm{Q}}_{B}^{i}, \overline{\mathrm{s}}_{B}\right)\right\rVert^{2}\right]+\mathbb{E}_{j \sim \mathcal{M}_{B}}\left[\left\lVert 1-C_{B}\left(\mathrm{Q}_{B}^{j}, \overline{\mathrm{s}}_{B}\right)\right\rVert^{2}\right] $$

• End-Effector Loss

  다른 skeleton에 대해서도 retargeting 할 수 있도록 훈련하는 것이 목적이지만 같은 수의 end-effector는 최소한 공유해야 한다. Humanoid로 치면 양발의 끝, 양손의 끝과 같은 점들은 공통으로 가지고 있어야 한다. 이를 활용하면 foot sliding도 완화하기는 하지만 완벽하게 없애지는 못하므로 보통 foot sliding은 IK post processing으로 처리해주게 된다.

  $$\tag{8} \mathcal{L}_{\mathrm{ee}}=\mathbb{E}_{i \sim \mathcal{M}_{A}} \sum_{e \in \mathcal{E}}\left\lVert \frac{V_{A_{e}}^{i}}{h_{A_{e}}}-\frac{V_{B_{e}}^{i}}{h_{B_{e}}}\right\rVert^{2} $$

따라서 full loss는 다음과 같다.

$$\tag{9} \mathcal{L}=\mathcal{L}_{\mathrm{rec}}+\lambda_{\mathrm{ltc}} \mathcal{L}_{\mathrm{ltc}}+\lambda_{\mathrm{adv}} \mathcal{L}_{\mathrm{adv}}+\lambda_{\mathrm{ee}} \mathcal{L}_{\mathrm{ee}} $$

Loss에 대한 가중치는 다음을 사용하였다고 한다. $$ \lambda_{\mathrm{ltc}}=1, \lambda_{\mathrm{adv}}=0.25, \lambda_{\mathrm{ee}}=2 $$

Experiments and Evaluations

동일 skeleton에 대한 성능을 intra-structural loss로, 다른 skeleton에 대한 loss를 cross-structural loss로 정의하였고 ground-truth에 대해서 position값의 평균오차로 계산하였다고 한다. 선으은 다음과 같다.

위의 표는 ablation study결과를 포함한다. 모든 loss를 적용하였을 때 cross-structural에서 가장 좋은 성능을 보이고 있음을 확인할 수 있다.

실제로 Figrue 11을 보면 다른 skeleton에 대해서도 다른 방법대비 자연스러운 모습을 보여준다.

Discussion and Future Work

논문에서는 common encoding space를 정의하는데 필요한 operator를 제시하였으며 이를 활용해 다른 skeleton에 retargeting이 이루어 질 수 있음을 보였다. 반면 T-pose가 크게 다른 skeleton에 대해서는 retarget이 잘 되지 않았다는 언급이 있다. 사실 이 부분은 다른 방법에서도 공통적으로 겪는 어려움일 것이다. 저자는 homeomorphic하지 않은 skeleton에도 적용할 수 있도록 보다 일반화된 primal skeleton에 대한 가능성을 언급하며 논문을 끝맺는다.

Bibliography

Aberman, Kfir, et al. “Skeleton-aware networks for deep motion retargeting.” ACM Transactions on Graphics (TOG) 39.4 (2020): 62-1.