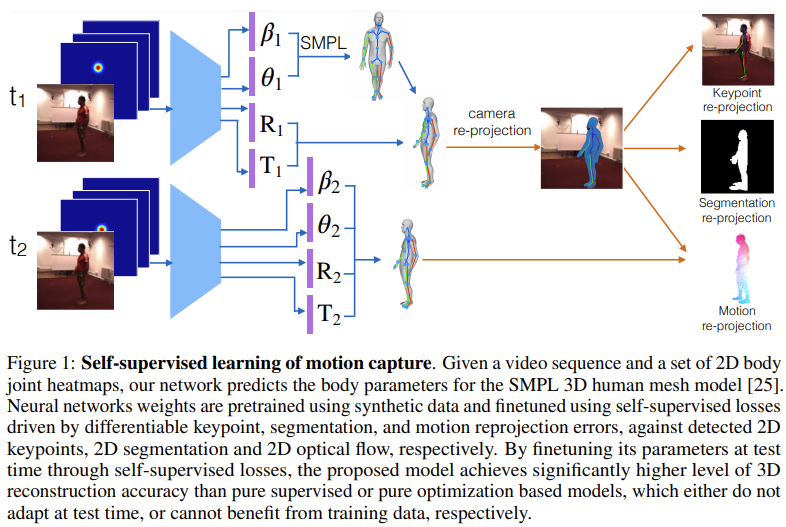
Self-supervised Learning of Motion Capture

Motion capture에 self-supervised learning을 적용해 단일 카메라의 정보(image)만을 사용해서도 사람의 3차원 mesh를 효과적으로 얻는 방법을 제안한다.

Abstract

논문에서 언급하는 당시 SOTA인 단일 카메라를 사용하는 motion capture는 최적화기반으로 이루어진다. 여기서의 최적화는 3D 사람모델의 parameter에 대한 최적화로 이를 re-projection한 결과는 비디오에서 측정한 person segmentation, optical flow, keypoint detection 등의 정보와 일치해야 한다. 즉, 이 차이가 줄어드는 방향의 최적화가 이루어진다. 하지만 이러한 최적화는 local minima에 쉽게 빠지므로 최적화를 돕기 위해 간혹 촬영장 사진에서 보이는 초록색 배경을 사용하거나 초기값의 튜닝, 여러 카메라의 정보 사용 등을 사용한다. 이 논문에서는 단일 카메라 입력을 사용해 motion capture하는 방법을 제안하였으며 learning based로 이루어진다.

최적화 기반의 방식은 mesh와 skeleton의 parameter를 직접 최적화하였지만 논문에서 제시하는 model은 하나의 카메라에서 얻은 RGB신호를 통해 neural network를 최적화해 3D shape과 skeleton configuration을 예측하도록 훈련한다. 논문제목에서 알 수 있듯이 이 과정에서 self-supervision이 사용된다. Self-supervision에 사용되는 정보는 (a) skeletal keypoints, (b) dense 3D mesh motion, (3) human-background segmentation이 있다.

Introduction

많은 motion capture관련 논문에서 언급하는 것처럼 이 논문에서도 좋은 motion 데이터를 얻는 작업이 쉽지 않음을 언급한다. 이 논문은 이러한 수고로움을 덜기 위해 이미지에서 3D mesh로의 mapping을 학습하는 방식을 제안한다.

We propose a neural network model for motion capture in monocular videos, that learns to map an image sequence to a sequence of corresponding 3D meshes.

애초에 supervised learning을 하는 것이 motion에서 어려운 이유는 3D mesh에 대한 annotation 데이터셋이 없기 때문이다. (large scale annotation of 3D human shapes in realistic video input is currently unavailable) 따라서 3D annotation이 없는 상황을 타개하기 위해서 human rendered model에 대해 데이터에 대한 supervised learning 방식과 3D keypoints, motion and segmentation, matching with corresponding detected quantities in 2D정보에 대해 3D-to-2D rendering 값을 self-supervised learning 방식으로 함께 사용한다. 즉, 레이블이 있는 데이터에 대한 지도학습과 3D정보를 2D로 projection한 값에 대한 self-supervised 방식을 조합했다고 생각하면 된다. 3D에서 2D에 대한 estimation값은 선행연구 결과를 사용하였다고 한다.

사람의 3D mesh model로는 유명한 SMPL을 사용한다. SMPL에서 global pose는 body parts가 이루는 각도인 $\theta$를 통해 정의되고, local shape을 조절하는 mesh surface parameter $\beta$에 의해 정의된다. 이렇게 pose와 surface parameter가 주어지면 mesh를 미분가능하게 해석적인 꼴로 나타낼 수 있으며 이렇게 얻어진 mesh는 원하는 위치로 rotation이나 translation을 줄 수도 있게 된다.

SMPL이 parameter에 의해서 pose를 만들어 내는, 다시 말해 rendering을 하는 역할을 하며 저자가 제시한 모델은 바로 이 rendering logic을 reverse engineering하는 것이다. 주어진 이미지들에 대해 사람을 감지하고 각 frame에서 사람의 형태에 대해 SMPL의 parameter, focal length, 3D rotation, 3D translation를 구성하는 모델이 이 논문에 주요 주제인 것이다.

2개의 연속적인 motion에 대해 3D mesh 예측값이 생기면 이 3D motion vector들을 각각 다르게 projection하고 2D optical flow vector와 비교한다.

$t_{1}$과 $t_{2}$에서는 각각 하나의 비디오와 2D body joint heatmap이 주어지게 된다. 이 정보를 사용해서 neural network는 SMPL 3D human mesh model의 body parameter들을 예측하게 된다. 이 때 학습에서 neural network의 weight은 레이블이 있는 데이터로 먼저 학습시켜 초기화시켜주고 keypoint, segmentation, motion reprojection error값들을 이용해 finetuning 해주게 된다. 물론 이 때 keypoint, segmentation, motion reprojection은 각각 2D keypoints, 2D segmentation, 2D optical flow로 예측된 값들이다. Self-supervised loss로 finetuning한 결과는 단순히 supervised나 optimization 기반 방식을 사용한 것보다 유의하게 좋은 accuracy를 달성했다고 한다.

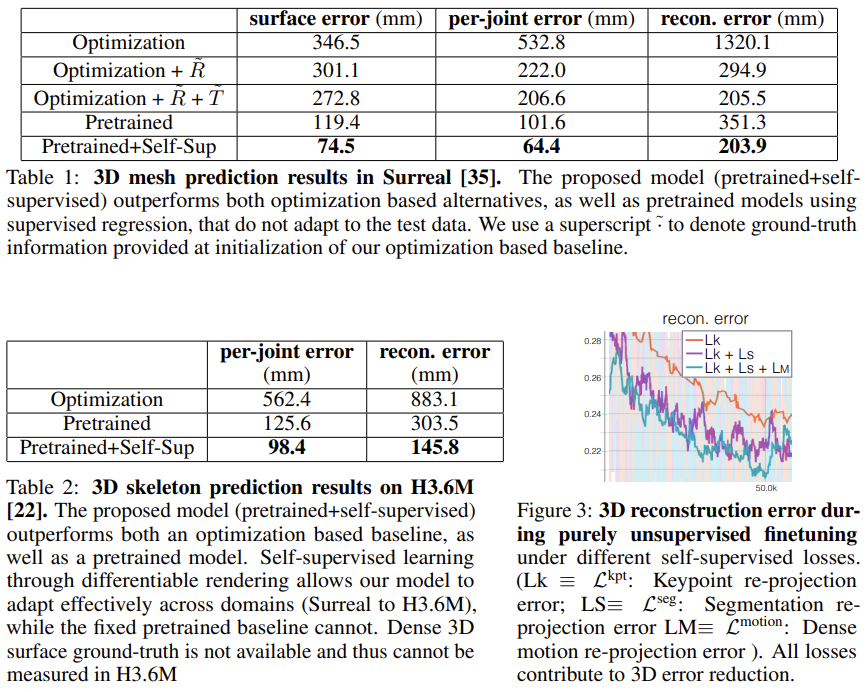
논문에서는 3D dense human shape tracking에 대해서 SURREAL과 H3.6M 데이터셋애 대해 정성적, 정량적 비교실험을 수행한다. 비교 대상은 optimization version과 supervised model이다.

Related Work

3D Motion Capture

3D motion capture는 보통 네 대 이상의 카메라를 사용하는 문제에 대해서는 좋은 성능을 보여왔으나 단일 카메라를 사용하는 경우에는 skeleton만 추출하는 문제도 쉽지 않은 문제로 여겨져왔다. 본 논문에서는 3D skeleton과 3D mesh estimation을 따로따로 해결하는 문제가 아닌 coupled된 문제로 인식하고 end-to-end로 differentiable한 formulation을 만들어 해결했다는 점을 강조한다.

3D human pose estimation

3D pose estimation은 이름 그대로 RGB image로부터 3차원 공간에서 사람의 pose를 추정하는 문제이다. FrankMocap의 README를 보면 어떤 문제를 풀고자 하는지 바로 이해할 수 있다.

Deep geometry learning

Geometry는 기하학적 구조를 의미하는 말로 사람의 pose도 사람이 가질 수 있는 조건에 conditioning된 geometry를 푸는 것으로 볼 수 있을 것이다. 이러한 측면에서 관련 연구를 언급한다.

Learning Motion Capture

앞서 소개된대로 neural network는 SMPL을 3D human shape에 대한 parameterized model로 바라본다. $\theta$, $\beta$는 각각 joint angle과 surface deformation parameters를 의미한다. 이 parameter들이 주어지면 다음의 식을 통해 정해진 개수($n=6890$)의 3D mesh vertex 좌표들을 얻을 수 있다. $\boldsymbol{X}_{i} \in \mathbb{R}^{3}$은 $i$번째 mesh vertex의 3차원 좌표를 의미한다.

$$\tag{1} \mathbf{X}_{i}=\overline{\mathbf{X}}_{i}+\sum_{m} \beta_{m} \mathbf{s}_{m, i}+\sum_{n}\left(T_{n}(\theta)-T_{n}\left(\theta^{*}\right)\right) \mathbf{p}_{n, i}$$

$\overline{X}_{i} \in \mathbb{R}^{3}$은 정지자세의 $i$의 위치이며 $\beta_{m}$은 skin surface blendshape의 blend coefficient, $\boldsymbol{s}_{m, i} \in \mathbb{R}^{3}$은 $m$번째 skin surface의 $i$번째 vertex, $\boldsymbol{p}_{n, i} \in \mathbb{R}^{3}$은 $n$번째 skeletal pose blendshape에서의 $i$번째 vertex, $T_{n}(\theta)$는 $n$번째 pose blendshape의 상대적인 회전행렬을 concatenate한 벡터로의 함수이며 $T_{n}(\theta^{*})$는 같은 함수인데 정지상태의 pose $\theta^{*}$를 입력으로 받는 함수이다.

Notation이 워낙 많다보니 장황한 느낌이 있는데 이는 어떤 pose에서 joint의 위치가 아닌 mesh vertex의 3차원 좌표를 의미하기 때문에 생기는 복잡한 표현이다. 사람의 피부위의 점들을 모두 표현하는 방식이다보니 직관적으로 바로 상상이 되지는 않는다. 다만 왼쪽부터 각 항의 의미를 보면 기준이 되는 rest pose에서 출발해 skin의 좌표를 잡고 이어 회전량과 offset이 곱해지는 걸로 보아 어떤 단계로 mesh vertex를 구성해가는지 짐작은 가능하다. 여기서 중요한 점은 식 (1)이 미분가능한 형태라는 점이다. 따라서 SGD와 같은 일반적인 deep learning framework을 적용하기가 쉽다.

논문에서 제시한 모델은 RGB image가 주어졌을 때 SMPL의 parameter $\beta, \theta$를 예측한다. 학습을 위해서는 앞서 언급한대로 synthetic monocular video 데이터셋을 사용한 superivision 방식과 3D keypoints, segmentation and vertex motion, matching with their 2D equivalents의 미분가능한 성질을 이용해 self-supervision 방식을 모두 사용한다.

Paired supervision from synthetic data

여러 차례 supervision 방식을 사용한다고 했는데 어떻게 사용했는지 알아보자. Surreal 데이터셋은 synthetic dataset이다. 사람이 직접 촬영한 것이 아닌 합성된 데이터 셋으로 SMPL 모델에 의해 생성된 캐릭터로 구성되어 있으며 Human H3.6M 데이터셋의 움직임을 사용한다. 이 데이터셋에서는 $\beta, \theta$에 접근할 수 있으므로 이 데이터들을 이용해 $\theta, \beta$를 pretrain 할 수 있다. 훈련시킬때는 일반적인 지도학습의 regression loss를 사용하면 된다. 지도학습 부분은 특별히 복잡한 과정 없이 Surreal 데이터셋 정보를 이용해 (1)식에 대한 regression의 loss로 훈련시켜 pretrained weight을 만든게 전부다.

Self-supervision through differentiable rendering

이제 self-supervision 부분이 남았다. Self-supervision은 3D-to-2D rendering된 결과와 keypoints, segmentation, optical flow의 2D estimation과의 차이를 줄이는 것이 목표다. Self-supervision은 train, test time에 모두 사용될 수 있으며 여기서는 모델의 weight을 test set에 가깝게 만드는데 사용된다.

Keypoint re-projection error

Keypoint re-projection의 과정을 생각해보자. 우선 image가 주어지고 이 image안의 사람에 대해 3D body joint를 예측하고 이를 다시 2차원으로 projection하면 이 결과가 바로 re-projection이 되며 실제 값과의 오차가 re-projection error가 된다. 다만 이 논문에서는 예측하고자 하는게 3D joint position이 아닌 3D mesh이다. 논문에서는 3D mesh vertices와 3D body joints를 다음과 같은 선형관계를 갖는 것으로 모델링하였다.

$$\tag{2} \boldsymbol{X}_{kpt}^{\top} = \boldsymbol{A} \cdot \boldsymbol{X}^{\top}$$

이 때, $\boldsymbol{X} \in \mathbb{R}^{4 \times n}$으로 $n$개의 mesh vertices에 대한 차원 좌표값을 나타낸다. 여기서 벡터크기가 4가 되는 이유는 추정컨데 바로 뒤에 다루어질 camera projection matrix가 $3 \times 4$ 형태라서 이에 맞추어주기 위함으로 생각한다. 3D-to-2D projection을 할 때 모델은 focal length, rotation of the camera, translation of the 3D mesh off the center of the image 총 세가지를 예측해야한다. Rotation은 Euler angle을 사용한다. $k$번째 keypoint에 대한 re-projection equation은 다음과 같다.

$$\tag{3} x_{k p t}^{k}=P \cdot\left(R \cdot \mathbf{X}_{k p t}^{k}+T\right)$$

$P=\operatorname{diag}\left(\left[f \quad f \quad 1 \quad 0\right]\right)$로 predicted camera projection matrix이며 $T=[T_{x} \quad T_{y} \quad 0 \quad 0]^{\top}$으로 object centering과 관련된 perturbation을 처리한다. 따라서 Keypoint projection error는 다음과 같다.

$$\tag{4} \mathcal{L}^{\mathrm{kpt}}=\left\lVert x_{k p t}-\tilde{x}_{k p t} \right\rVert_{2}^{2}$$

$\tilde{x}_{kpt}$는 실제값 또는 detected 2D keypoint 값이다.

Motion re-proejction error

두 개의 sequence $I_{1}, I_{2}$가 주어졌을 때, 앞의 모델은 각각에 대해 $\beta, \theta, R, T$를 예측하게 된다. 식 (1)을 통해 $i=1, \cdots, n$에 대해 $\boldsymbol{X}_{1}^{i}$, $\boldsymbol{X}_{2}^{i}$를 얻을 수 있다. 이 3차원 mesh vertices는 pixel로 (3)에 의해 projection하면서 $\left(x_{1}^{i}, y_{1}^{i}\right), i=1 \cdots n,\left(x_{2}^{i}, y_{2}^{i}\right), i=1 \cdots n$로 옮겨진다. 따라서 3차원 모션에서 예측한 2D body flow는 다음과 같이 나타낼 수 있다.

$$\left(u^{i}, v^{i}\right)=\left(x_{2}^{i}-x_{1}^{i}, y_{2}^{i}-y_{1}^{i}\right), i=1 \cdots n$$

2차원 이미지에서 대응하는 mesh의 변위벡터의 집합으로 읽을 수 있다. 모션은 결국 pose의 순차적 이동이므로 변위의 집합으로 모션을 만들어 낼 수 있다. 이렇게 2차원 optical flow로 추정한 것을 $\mathcal{OF} = (\tilde{u}, \tilde{v})$라고 하자. 여기서 말하는 optical flow는 FlowNet 2.0에서 제시한 방법이다. 속도벡터정도의 의미를 부여할 수 있을 것이다. $\mathcal{OF}(x_{1}^{i}, y_{1}^{i})는 differentiable warping으로 부터 얻어지는 결과이다. 이러한 방식으로 motion re-projection error를 다음과 같이 정의한다.

$$\mathcal{L}^{\text {motion }}=\frac{1}{\mathbf{1}^{T} \mathbf{v}} \sum_{i}^{n} \mathbf{v}^{i}\left(\left\lVert u^{i}\left(x_{1}^{i}, y_{1}^{i}\right)-\tilde{u}\left(x_{1}^{i}, y_{1}^{i}\right)\right\rVert_{1} + \left\lVert v^{i}\left(x_{1}^{i}, y_{1}^{i}\right)-\tilde{v}\left(x_{1}^{i}, y_{1}^{i}\right) \right\rVert_{1}\right)$$

Segmentation re-projction error

이름대로 주어진 이미지의 segmentation이 잘 되었는지를 확인하는 error로 Chamfer distance라는 개념을 도입한다. Chamfer distance는 segmentation된 픽셀을 1 아닌 값을 0이라고 할 때, 예측한 segmentation값이 가장 가까운 1이어야 하는 픽셀로 부터 얼마나 떨어져 있는지를 나타내는 matrix이다. Model projected segmentation을 $M$으로, figure-ground binary image segmentation을 $I$라고 하면 다음과 같은 element-wise곱의 합으로 정의한다.

$$\mathcal{L}^{\mathrm{seg}}=\mathcal{S}^{M} \otimes \mathcal{C}^{I}+\mathcal{S}^{I} \otimes \mathcal{C}^{M}$$

이 때, $x_{2d}^{i}, i \in 1, \cdots, n$을 model projected vertex pixel좌표의 집합이라고 하고 $x_{seg}^{p}, p \in 1, \cdots, m$을 segmentation map $S^{I}$의 중심으로 정렬된 pixel의 집합이라고 하면 다음과 같은 projected segmentation loss를 정의할 수 있다.

$$\tag{5} \mathcal{L}^{\text {seg-proj }}=\underbrace{\sum_{i=1}^{n} \min_{p}\left\lVert x_{2 d}^{i}-x_{s e g}^{p}\right\rVert_{2}^{2}}_{\text {prevent over-coverage }}+\underbrace{\sum_{p}^{m} \min_{i}\left\lVert x_{s e g}^{p}-x_{2 d}^{i}\right\rVert_{2}^{2}}_{\text {prevent under-coverage }} $$

첫 번째 term은 모델에 의해 projection된 segmentation 중 image segmentation가 cover하는 영역이며 두 번째 term은 image segmentation의 영역이 모델에 의한 projected segmentation에 의해 cover되는 영역이다. 대체로 $i$ notation은 기존 이미지에 바로 segmentation이 적용된 결과로, $m$ notation은 모델을 거쳐 re-projection된 결과라는 것을 상기하고 보면 이해하기가 조금 더 편해진다.

여기까지 오면서 개인적으로는 수식의 의미에 매몰되다 보니 정작 중요한 self-supervised에 대한 내용이 잘 안느껴졌었다. 정리해보면 위 Figure 2에서 $\mathcal{L}^{\text{kpt}}$가 왼쪽에 표현된다. $\tilde{x}$는 2D 이미지 그 자체에 대한 keypoint혹은 keypoint detection의 결과이고 $x$는 Figure 1의 모델을 거쳐서 re-projection한 결과이다. 여기서 실제 정답 keypoint는 주어지지 않으며 굳이 학습의 방향을 말한다면 이미지에 바로 적용한 keypoint detection결과가 정답과 유사한 역할을 준다고 볼 수 있을 것이다. 요점은 정답은 주어지지 않고 다른 알고리즘의 도움을 받아 keypoint에 대한 mapping을 만들어간다는 측면에서 self-supervision을 하고있다고 볼 수 있다. 나머지 $\mathcal{L}^{\text{seg}}$와 $\mathcal{L}^{\text{motion}}$도 같은 방식으로 self-supervision을 수행한다.

Experiments

실험은 Surreal과 H3.6M 두 데이터셋에 대해 수행된다. 실험의 목적은 Surreal에서 H3.6M으로 Figure 1모델이 domain transfer가 성공적으로 된다는 것을 보이는 것이다. 따라서 Surreal 데이터셋에 대해서는 supervision을 충분히 활용하지만 H3.6M에 대해서는 3D ground truth를 전혀 사용하지 않는다.

Figure 1의 모델은 우선 skeleton과 surface parameter를 Surreal 데이터 셋에 대해 supervised 방식으로 학습시킨다. 그리고 Section 3의 self-supervision방식을 Surreal과 H3.6M 두 테스트 셋에 대해 수행한다. Self-supervision의 경우는 2D keypoint와 segmentation의 ground truth를 사용한다. Segmentation의 경우 Surreal은 매우 정확한 결과를 보여주지만 H3.6M에서는 단순히 배경을 빼는 방식으로 만들다 보니 segmentation의 품질이 상당히 떨어진다.

위 Figure 4를 보면 위의 네 개는 Surreal, 아래 네 개는 H3.6M이다. Segmentation ground truth를 보면 H3.6M의 품질이 훨씬 낮은 것을 볼 수 있다. 특히 아래에서 세번째와 가장 마지막 행을 보면 segmentation 품질이 좋지 않다는 것을 쉽게 확인할 수 있다. 하지만 이 논문에서 제시한 모델을 사용하면 6번째 열에서 볼 수 있는 것처럼 훨씬 개선된 품질의 mask를 얻을 수 있고 다른 예측결과들도 실제 input과 비교해볼 때 상당한 품질의 결과를 만들어 낸 것을 볼 수 있다.

Evaluation metric

정량적 비교를 위해 per-joint error, reconstruction error, surface error를 per-joint error와 surface error는 L2 loss를 사용하며 reconstruction error는 다음의 식을 사용한다. $T$는 3D translation을 의미한다.

$$ \min_{T} \frac{1}{K} \sum_{k=1}^{K} \left\lVert \left(\mathbf{X}_{k p t}^{k}+T\right)-\left(\tilde{\mathbf{X}}_{k p t}^{k}\right) \right\rVert_{2} $$

Ablation study는 다음 모델들과 비교하며 이루어진다.

• Pretrained: supervised learning만 사용한 것으로 self-supervised adaptation이 사용되지 않는다.
• Direct optimization: self-supervision을 사용하지만 neural network대신에 body mesh parameter인 $(\theta, \beta)$, rotation $R$, translation $T$, focal length $f$를 직접 최적화한다.

논문에서 제시한 방식이 다른 방식보다 큰 폭의 성능향상을 내고 있음을 보여준다.

Conclusion

이 논문에서는 dense human 3D body tracking을 learning based로 해결하는 방법을 제시하였다. 크게 supervised learning part와 self-supervised learning part로 구성된다. Supervised learning에서는 synthetic data(Surreal)에 대해 사전학습을 시켜 제시한 모델이 적절한 weight을 갖도록 해준다. 그 다음에 H3.6M 데이터로 self-supervision을 사용해 domain transfer를 한다. 이 때, self-supervised 방식을 사용하기 위해 mesh motion, keypoints, segmentation에 대해 미분가능한 rendering 방식을 제시하고 이 결과를 2D equivalent quality와 비교해 loss를 만들어 fine tuning을 하게 된다. 2D equivalent quality는 이미 나와있는 2D estimation 알고리즘들을 이미지에 바로 적용하는 방식으로 사용한다.

Self-supervised가 가지는 장점인 unlabelled 데이터를 활용해 baseline 알고리즘들 보다 성능을 향상시키는 것을 보여주며 이는 3D annotation이 매우 힘든 motion capture에서 매우 유용한 성과라고 생각한다.

Bibliography

Tung, Hsiao-Yu Fish, et al. “Self-supervised learning of motion capture.” arXiv preprint arXiv:1712.01337 (2017).