Reinforcement Learning as One Big Sequence Modeling Problem

강화학습은 주로 MDP로 문제 formulation을 한다. MDP는 discrete-time에 대한 stochastic process를 다루는 유용한 도구이다. 생각해보면, sequence modeling도 유사한 점이 있음을 알 수 있다. 이 논문에서는 sequence modeling에서 좋은 성능을 보여주며 de facto standard가 된 Transformer를 강화학습에 적용하려는 시도를 보여준다.

Abstract

강화학습의 목적은 기대 보상의 총합, return을 최대화하는 좋은 policy를 찾는 것이다. 이 때 정책은 single-step policy를 추정하는 문제이다. 여기서 single-step은 Markov property를 의미하는 단어이다. 논문의 핵심은 강화학습을 sequence modeling 문제로 바라봄으로써 높은 보상을 받는 일련의 action을 예측하는 문제로 접근하는 것이다. 모델은 sequence modeling에서 SOTA를 보여주고 있는 Transformer를 사용하므로 여타 강화학습논문처럼 모델이 어떤구조인지보다는 지금까지의 강화학습, 특히 imitation learning이나 goal-conditioned RL, offline RL의 framework에 sequence modeling framework를 어떻게 적용할 수 있는지에 초점이 맞추어진다.

Introduction

이 논문은 강화학습 문제를 어떻게 sequence modeling framework으로 접근할 것인지에 대해 다루며 따라서 강화학습의 기본적인 내용을 이해한 상태로 보아야 읽기가 쉽다.

We can also view reinforcement learning as analogous to a sequence generation problem, with the goal being to produce a sequence of actions that, when enacted in an environment, will yield a sequence of high rewards.

이 논문은 다음의 질문으로 함축할 수 있다.

Does the toolbox of contemporary sequence modeling itself provide a viable reinforcement learning algorithm?

강화학습의 학습과정은 $s, a, r, \cdots$와 같은 trajectory를 만들게 되고 이 논문에서는 이 trajectory를 seqeunce로 취급한다. 강화학습의 model-based의 trajectory optimizer의 역할에 대응하는 것으로는 beam search를 사용한다.

저자는 제안한는 방법의 이름은 Trajectory Transformer로 이름 자체에서도 trajectory를 sequence로 처리할 것임이 잘 드러나는 좋은 명명이라 생각한다. Beam search방법을 강화학습에 맞도록 NLP에서 처럼 높은 likelihood를 좇는게 아닌 높은 보상을 받도록 바꾸어주며 이 방법으로 offline benchmark에서 기존 강화학습의 SOTA방법들과 비등한 결과를 얻었다고 한다. 기존의 sequence modeling을 강화학습에 적용하였을 뿐만 아니라 unsupervised learning의 이점을 강화학습에도 도입하였다는데 의의가 있다.

Related Work

앞서, sequence model을 강화학습에 적용하는 방법의 연구가 없었던 것은 아니다. 다만 이전 방법들은 강화학습의 기본적인 방법론을 그대로 이용하면서 trajectory의 representation쪽을 다루었다면 이 논문에서는 가능한한 모든 강화학습의 모든 pipeline을 sequece modeling의 방법으로 바꾸는 것이다. 이렇게 하는 중요한 이유는 강화학습문제를 알고리즘의 고도화보다 sequence model이 갖는 장점인 풍부한 representational capacity을 활용해보기 위함이라고 한다. Trajectory Transformer는 하나의 high-capacity sequence model을 훈련시켜 상태, 행동, 보상의 joint distribution을 표현하며 predictive model이나 behavior policy (imitation learning), behavior constraint (offline RL)에 사용할 수 있다고 한다. 참고로 imitation learing은 말 그대로 사람과 같은 expert를 잘 따라하는 학습기법으로 behavior cloning과 inverse reinforcement learning과 같은 방법이 있으며 offline RL은 online RL처럼 환경과 상호작용하는 것이 아니라 이전의 경험들만을 사용해 하는 방식으로 상호작용없이 trajectory 정보만을 사용해 좋은 policy를 학습하는 task를 일컫는다.

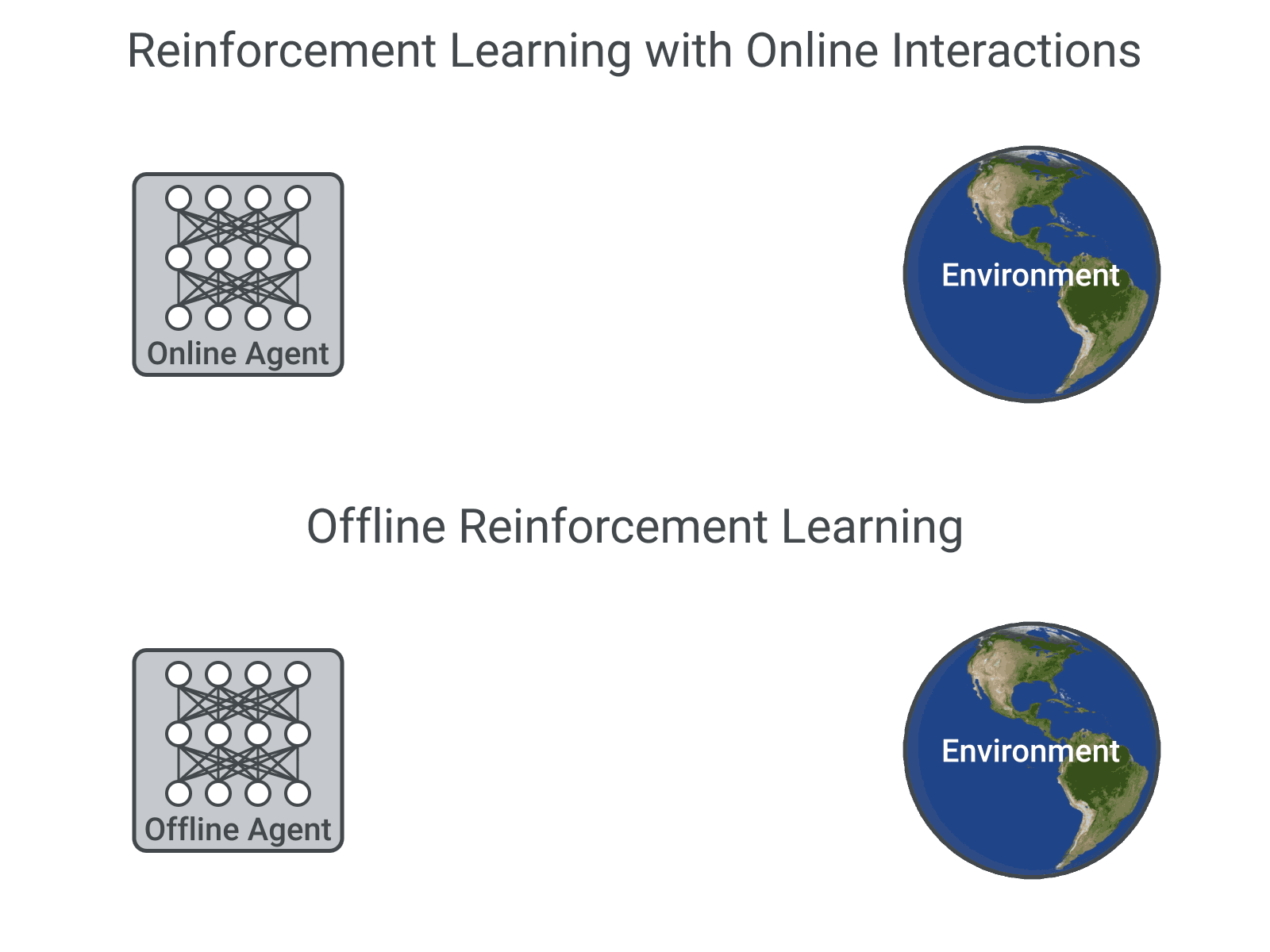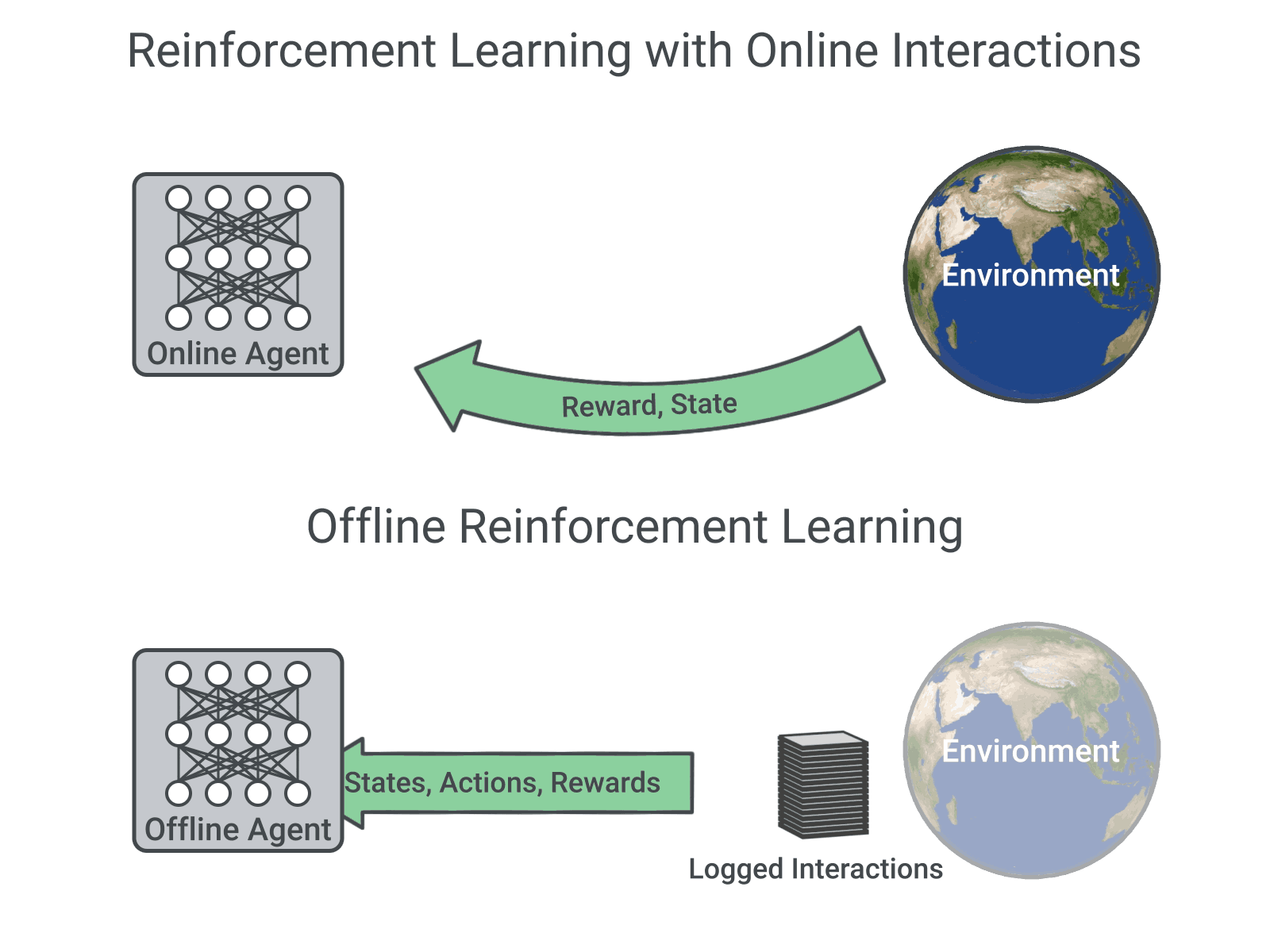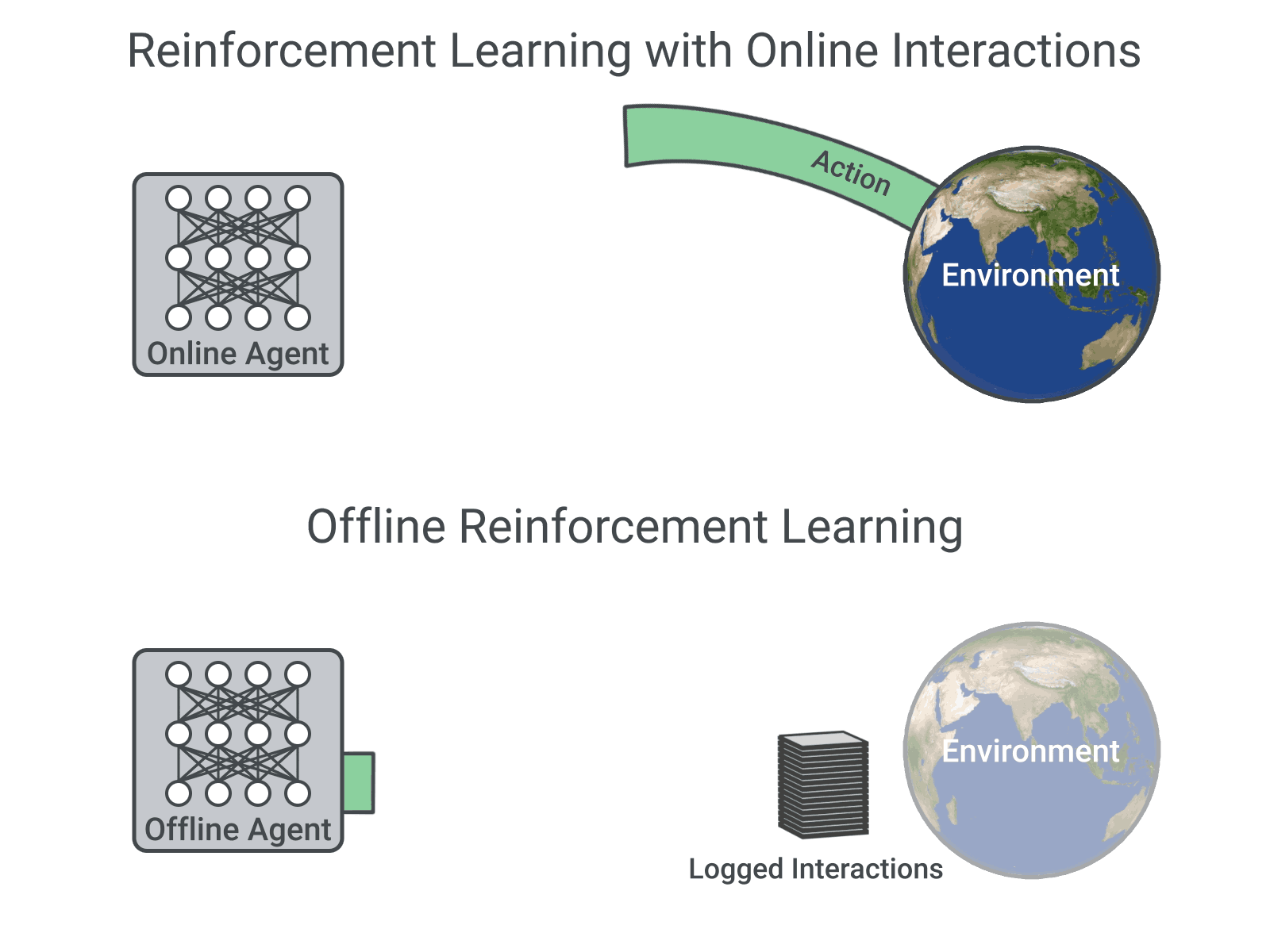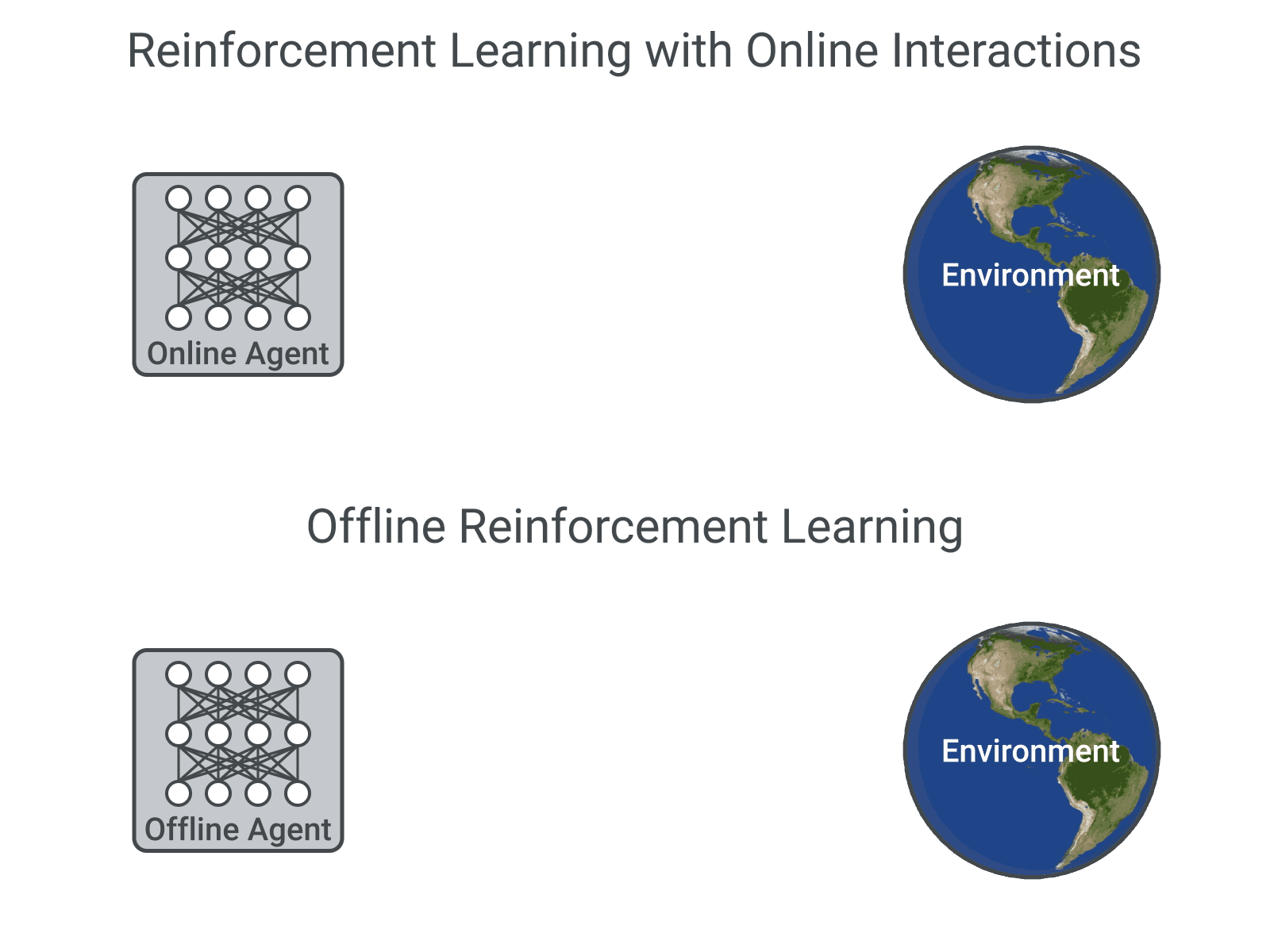
Trajectory transformer는 기존 강화학습 방법 중에서 model-based 방법과 유사하다. Model-free와는 다르게 model-based learning은 환경의 역할을 해주는 model이 있어 이를 사용해 planning을 하게 된다. 비슷한 목적으로 trajectory transformer는 beam search algorithm을 사용해 action을 선택하게 된다. 그리고 상태와 행동을 학습하는 과정이 언어모델로 강화학습 framework처럼 명시적인 exploration이 없으므로 행동에 대해 in-distribution bias가 자연스럽게 생기게 된다. 논문에서는 이러한 점을 explicit pessimism을 피할 수 있는 장점으로 언급하는데 개인적으로는 exploration측면에서는 충분히 다양한 예제를 보지 못할 것으로 생각되어 장점보다는 trade-off에 가깝지 않나 생각한다. 이 section에서는 강화학습 알고리즘의 component들을 sequence model인 Transformer로 치환하였다는 내용을 언급한다.

Reinforcement Learning and Control as Sequence Modeling

제시한 Trajectory Transformer를 소개한다. 서두에 Trajectory Transformer는 구현측면에서는 model과 search trajectory가 NLP에서 사용하는 것과 거의 동일하다고 강조한다. 여러번 언급되듯 이 논문의 핵심은 강화학습 benchmark에서 SOTA를 찍었다는 식이 아니라 sequence modeling의 방법들을 강화학습에 적용하였다는 것이며 NLP의 모델을 거의 유사하게 가져왔으므로 주의깊게 보아야 할 부분은 architecture가 어떻게 생겼는지보다는, 어떻게 강화학습의 continuous state, action과 같은 trajectory data를 sequence modeling에 사용할 수 있도록 설계하였는지이다.

Trajectory Transformers

Trajectory Transformer에서 가장 중요한 부분은 어떻게 trajectory data를 unstructured sequence로 처리할 것인지이다. 언어모델을 생각해보면 각 단어는 부여받은 vector로 문장을 구성하게 되는데 이 단어 벡터에 대응되는 표현이 필요해진다.

예를 들어 trejectory $\tau$가 $N$개의 상태를 갖고 $M$개의 행동을 가지며 scalar rewards를 받는 구조로 되어있다고 해보자. 이를 표현하면 다음과 같다.

$$ \tau=\left\lbrace\mathbf{s}_{t}^{0}, \mathbf{s}_{t}^{1}, \ldots, \mathbf{s}_{t}^{N-1}, \mathbf{a}_{t}^{0}, \mathbf{a}_{t}^{1}, \ldots, \mathbf{a}_{t}^{M-1}, r_{t}\right\rbrace_{t=0}^{T-1} $$

Subscript $t$는 timestep을 superscript는 각 상태와 행동의 차원을 나타낸다. 연속적인 상태와 행동은 각 차원에서 discretization을 필요로 한다. Discretization은 다음과 같이 차원마다 정해진 수의 bin을 사용해 표현한다.

어떤 상태가 연속값으로 $s_{t}^{i} \in [l^{i}, r^{i})$라고 해보자. 이 때 $s_{t}^{i}$의 tokenization은 다음과 같다.

$$\tag{1} \bar{\boldsymbol{s}}_{t}^{i} = \left\lfloor V \frac{\boldsymbol{s}_{t}^{i} - l^{i}}{r^{i} - l^{i}} \right\rfloor + V_{i}$$

$V_{i}$는 상태들이 겹치지 않게 해도록 만들어주는 offset이고 각 상태는 가질 수 있는 범위에서 normalize한 뒤(minmax norm) per-dimension vocabulary size $V$를 곱해주게 된다. Action token $\bar{\boldsymbol{a}}_{t}^{j}$도 비슷한 원리로 offset을 $V \times (N + j)$만큼 주게 된다. Discretized reward $\bar{r}_{t}$는 $V \times (N + M)$으로 offset을 준다. 겹치지 않게 하려다보니 순서대로 상태차원의 수, 행동차원의 수 만큼 비켜서 더하고 있음을 알 수 있다.

이를 정리해 보면 매 timestep마다 상태, 행동, 보상의 차원수에 해당하는 sequence가 생성이되므로 timestep $T$만큼 진행되면 $T \times (N + M + 1)$의 sequence가 생성된다. 저자가 언급하기를 이러한 표현방식은 비효율적으로 보일 수 있지만 Gaussian transition과 같은 simplifying assumption을 사용하지 않고 trajectory의 분포를 효과적으로 모델링할 수 있게 해준다고 한다. Continuous state를 다루는 문제에서 분포를 Gaussian으로 잡는 경우를 많이 보았는데 이 때마다 분포가정에 대해 의문이 있었다. 이런 측면에서, 논문에서 제시한 방식은 분포가정이 없어 충분히 설득력있다고 생각된다.

모델의 기본적인 구조는 GPT에서 사용된 Transformer decoder이다. 다만 여기서는 large-scale 언어 모델에서 사용하는 것보다 작은 구조를 사용하였다고 한다. 4개의 layer와 self-attention heads를 사용한 구조가 사용되었다. 훈련과정에서는 teacher-forcing procedure를 사용하였다고 한다. teacher-forcing은 훈련과정에서 초기 학습향상을 위해 순서예측을 할 때 순차적으로 예측값을 넣어주는 것이 아닌 ground truth를 넣어주어 학습효율을 올리는 방법이다. Trajectory Transformer의 parameter를 $\theta$라고 할때, induced conditional probability를 $P_{\theta}$로 표현하며 쉽게 생각해 predicted token으로 보면 된다. 학습에서 최대화하여야하는 objective는 다음과 같이 표현된다.

$$ \mathcal{L}(\bar{\tau})=\sum_{t=0}^{T-1}\left(\sum_{i=0}^{N-1} \log P_{\theta}\left(\overline{\mathbf{s}}_{t}^{i} \mid \overline{\mathbf{s}}_{t}^{<i}, \bar{\tau}_{<t}\right)+\sum_{j=0}^{M-1} \log P_{\theta}\left(\overline{\mathbf{a}}_{t}^{j} \mid \overline{\mathbf{a}}_{t}^{<j}, \overline{\mathbf{s}}_{t}, \bar{\tau}_{<t}\right)+\log P_{\theta}\left(\bar{r}_{t} \mid \overline{\mathbf{a}}_{t}, \overline{\mathbf{s}}_{t}, \bar{\tau}_{<t}\right)\right) $$

여기서 $\bar{\tau}_{<t}$는 timestep 0에서부터 timestep $t-1$까지의 tokenized trajectory에 대한 표기이다.

이 식은 바깥에서부터 보면 이해하기가 용이하다. 우선 가장 바깥쪽에서 $T$만큼의 timestep마다 계산한 각각을 더한걸 최대화하는 것이 목표이다. 이 때 내부의 값은 $+$를 기준으로 나누어 보면 각각 다음의 합이다.

• 각각의 상태마다 이전 tokenized trajectory이 주어졌을 때 현재 상태의 tokenized 상태에 대해서 이전 dimension에 대해 다음 dimension의 tokenized state가 되는 확률의 $\log$를 더하게 된다. 결과적으로 상태에 대한 likelihood 추정이라고 생각한다.
• 위와 완전히 동일한 내용을 action에 대해서 적용한다.
• 위와 완전히 동일한 내용을 reward에 대해서 적용한다.

즉, 기본 단위인 한 상태의 $s, a, r$에 대한 likelihood 계산으로 이해하였다. 이를 최대화 하는 것이므로 Maximum likelihood의 아이디어를 따라가는 식이라고 생각한다. 의아한 부분은 각각의 likelihood를 이전 상태, 행동에 대해 autoregressive한 방식으로 계산하는데, 각각의 상태와 행동이 순차적인 의미를 갖지는 않음에도 이렇게 계산한다는 것이다. Pixel RNN과 같은 논문에서도 픽셀간의 autoregressive한 계산이 있는데 굳이 의미를 부여하면 어느정도 두 방법이 바라보는 시계열처리 기법의 유사성이 있지 않나 생각해보았다.

다만 이를 그냥 계산할 수는 없는게 self-attention은 quadratic complexity를 가지므로 반드시 conditioning token의 수를 제한해야한다. 논문에서는 512로 설정했다고 한다. 이는 다시 말해 $\frac{512}{N + M + 1}$개의 transition을 반영한 self-attention을 수행한다는 의미가 된다. 이 부분은 꽤 단점이 될 수 있는게 상태의 수와 행동의 수에 대해서 discretization을 모두 한 결과가 $N + M + 1$인데 이 값이 512까지가 최대치라는 점이다. Discretization임을 감안하면 처리할 수 있는 horizon이 아주 길게까지 처리하는건 한계점이 있어 보인다.

Transformer Trajectory Optimization (TTO)

여기서는 Trajectory Transformer가 어떻게 control문제에 적용할 수 있는지를 다룬다. 여기서 말하는 control은 정책개선과 같이 정책을 향상시키는 방법으로써의 control이다. 논문에서는 크게 세가지 setting을 다룬다.

• Imitation learning
• Goal-conditioned reinforcement learning
• Offline reinforcement learning

모두 Beam search에 기반하고 있으며 위의 순서대로 sequence model decoding algorithm(여기서는 Beam search)에서 modification이 점점 이루어지게 된다. 여기 언급된 모든 방식을 Transformer tranjectory optimization(TTO)라고 통칭한다.

Imitation Learning

Imitation learning일 때의 setting은 간단하다. trajectory transformer가 이미 expert(training data)로부터 학습한 모델이므로 시작상태인 $\boldsymbol{s}_{0}$부터 예측을 하기만 하면 된다. 이는 sequence modeling의 목적과 완전히 일치하며 beam search를 변경 없이 그대로 사용하면 된다. 이 과정은 Algorithm 1으로 기술할 수 있다.

알고리즘의 결과로 얻는 것은 데이터분포에서 가장 높은 확률을 갖는 tokenized trajectory $\bar{\tau}$이다. 이러한 방법은 behavior cloning의 model-based 버전처럼 생각해 볼 수 있다. 예측할 sequence length를 action dimension만큼 잡으면 autoregressive policy를 사용한 behavior cloning과 같아지게 된다.

Goal-conditioned reinforcement learning

Transformer 구조를 보면 causal attention mask를 사용해서 미래의 데이터를 가려주는 부분이 있다. 강화학습 framework관점에서 trajectory prediction context에서는 physical causality를 반영하는 의미를 부여할 수 있다. 하지만 미래정보를 알고 있는 상황에서의 과거에 대한 conditional probability는 앞으로 일어나기를 바라는 future context의 의미를 가지므로 유의미하게 사용할 수 있다. 내용은 복잡하지만 결과적으로 도착하고자 하는 상태의 정보를 학습에 사용하겠다는 것이 goal-conditioned의 의미이다.

만약 trajectory의 끝부분이 도착하고자 하는 future context라면, 다음상태의 trajectory를 다음과 같이 확률로써 decode할 수 있다.

$$ P\left(\overline{\mathbf{s}}_{t}^{i} \mid \overline{\mathbf{s}}_{t}^{<i}, \bar{\tau}_{<t}, \overline{\mathbf{s}}_{T-1}\right) $$

위의 형태를 goal-reaching method로 바로 사용할 수 있다. 식을 보면 가장 오른쪽에 항상 도착하고자 하는 상태로 conditioning하고 있음을 알 수 있다. 이렇게 항상 final goal state를 conditioning하면 lower-diagonal attention mask를 다음과 같이 만듦으로써 mask를 고정시킬 수 있다.

$$ \lbrace\overline{\mathbf{s}}_{T-1}, \overline{\mathbf{s}}_{0}, \overline{\mathbf{s}}_{1}, \ldots, \overline{\mathbf{s}}_{T-2}\rbrace $$

이렇게 goal state를 sequence의 맨 앞으로 가져다 놓음으로써 모든 예측에서 goal state을 attend 하게 하면서 기존 attention 구현을 유지할 수 있게 된다. 이러한 방식의 goal conditioning은 기존의 goal conditioned policy나 model-free RL에서의 relabeling technique과 유사점이 있다고 한다. 참고로 relabeling technique에서 HER를 인용하고 있다. 논문에서 제시한 framework에서 goal-conditioned 조건을 반영하는 것은 복잡하지 않다. 마찬가지로 sequence labeling framework을 그대로 사용하면서 주어진 evidence에 대해 가장 가능성이 높은 sequence를 예측하게 된다.

Offline reinforcement learning

Algorithm 1에서 소개된 beam search는 데이터 분포의 확률로 sequence optimization을 하게 된다. Objective식에서 token prediction에 대한 log-probabilities를 predicted reward signal로 바꾸게 되면 앞서 제시된 Trajectory Transformer와 reward-maximizing behavior를 찾는 search strategy(beam search)를 그대로 사용할 수 있게 된다. 이 방식은 사실상 기존 제시한 방법에서의 beam search에서 transition의 log-probability를 optimality의 log-probability로 대체하는 효과를 갖는다. 최적성(optimality)라는 단어를 사용한 이유는 predicted reward signal부분이 결과적으로 보상의 합(sum of rewards)가 되기 때문이다.

그럼 기존의 token prediction부분을 reward prediction으로 바꾸었으므로 beam-search는 reward-maximizing procedure가 된다. 문제는 beam search에서 얼마나 많은 후보군을 둘 지 결정할 때 이는 당장 만들어내는 인접한 예측값들의 likelihood, 여기서는 보상의 합이 되므로 근시안적이 된다는 것이다. 논문에서는 discount factor와 같은 개념을 적용해 이 문제를 다룬다. Training trajectory에서 매 transition마다 reward-to-go라는 다음의 성질을 추가해준다.

$$ R_{t}=\sum_{t^{\prime}=t}^{T-1} \gamma^{t^{\prime}-t} r_{t^{\prime}} $$

이 reward-to-go는 더하는 형태로 기존 값과 합치는게 아니라 말 그대로 augment하는 개념으로 다른 값들 처럼 discretization을 거치고 immediate reward를 예측할 때 함께 계산되도록 만들어 주었다고 한다. Monte Carlo value estimate에 대해 greedy한 action selection은 online data collection을 하지 않는 상황에서는 sample efficiency가 떨어지고 suboptimal에 잘 빠지는 것으로 알려져있다. 저자는 reward-to-go 추정을 beam search를 guiding하는 heuristic으로 사용하였다고 하며 따라서 이 추정치가 정확하지는 않다고 밝힌다. 추가로 offline RL에서 이러한 reward-to-go 추정은 behavior policy의 가치를 추정하지만 일반적으로 TTO를 통해 달성하는 가치값과 일치하지는 않는다고 한다. Heuristic을 사용하기는 하지만 reward-to-go를 trajectory에 augmenting해 예측하는 방식은 classifier를 훈련하는 정도로 간단하다고 한다.

이러한 setting에서 제시한 transformer는 reward와 reward-to-go를 매 $N + M + 1$ token 마다 예측하게 된다. (즉, 한 timestep의 예측 token마다 예측한다는 뜻이다) 여기서 모든 중간단계의 token을 log-probabilities를 사용해 sampling한다. 구체적으로는 full transition인 $(\bar{\boldsymbol{s}}_{t}, \bar{\boldsymbol{a}}_{t}, \bar{r}_{t}, \bar{R}_{t})$을 likelihood maximizing beam search를 사용해 sampling하고 이 transition을 sequence model에서의 vocabulary처럼 사용한다. 이렇게 탐색된 결과 중 cumulative reward + reward-to-go 추정치의 합이 큰 경우를 걸러내면 된다.

이 section에서는 sequence modeling으로 model-based planning algorithm을 만들고 predictive model과 reward-maximizing trajectory로 어떻게 사용하는지를 보였다. 저자는 이러한 접근이 가능한 것은 sequence modeling와 trajectory optimization과 밀접한 관련이 있기 때문이라고 말한다. 동시에, 중요한 차이점을 언급하는데, 행동과 상태를 함께 모델링하고 같은 절차로 sampling을 하는 것은 모델이 out-of-distribution 행동을 사용하는 것을 억제하게 만든다고 한다. 행동을 상태에 의존하지 않는 unconstrained optimization variable로 취급하는 것은, learned model을 사용한 maximizing reward 문제를 classifier에 대한 adversarial example을 찾는 것과 유사한 문제로 만들어주어 model exploitation을 용이하게 만들어 준다.

Experiments

실험에선는 다음 두 가지를 집중적으로 확인한다.

• Trajectory Transformer가 long-horizon predictor로써 일반적인 dynamic model parameterization 모델들과 accuracy가 대등하게 나오는가?
• Offline RL, imitation learning, goal-reaching의 문제에서 제시한 sequene modeling tool인 beam search algorithm이 control algorithm으로 사용가능한가?

당연히 두 질문의 답은 그렇다이다.

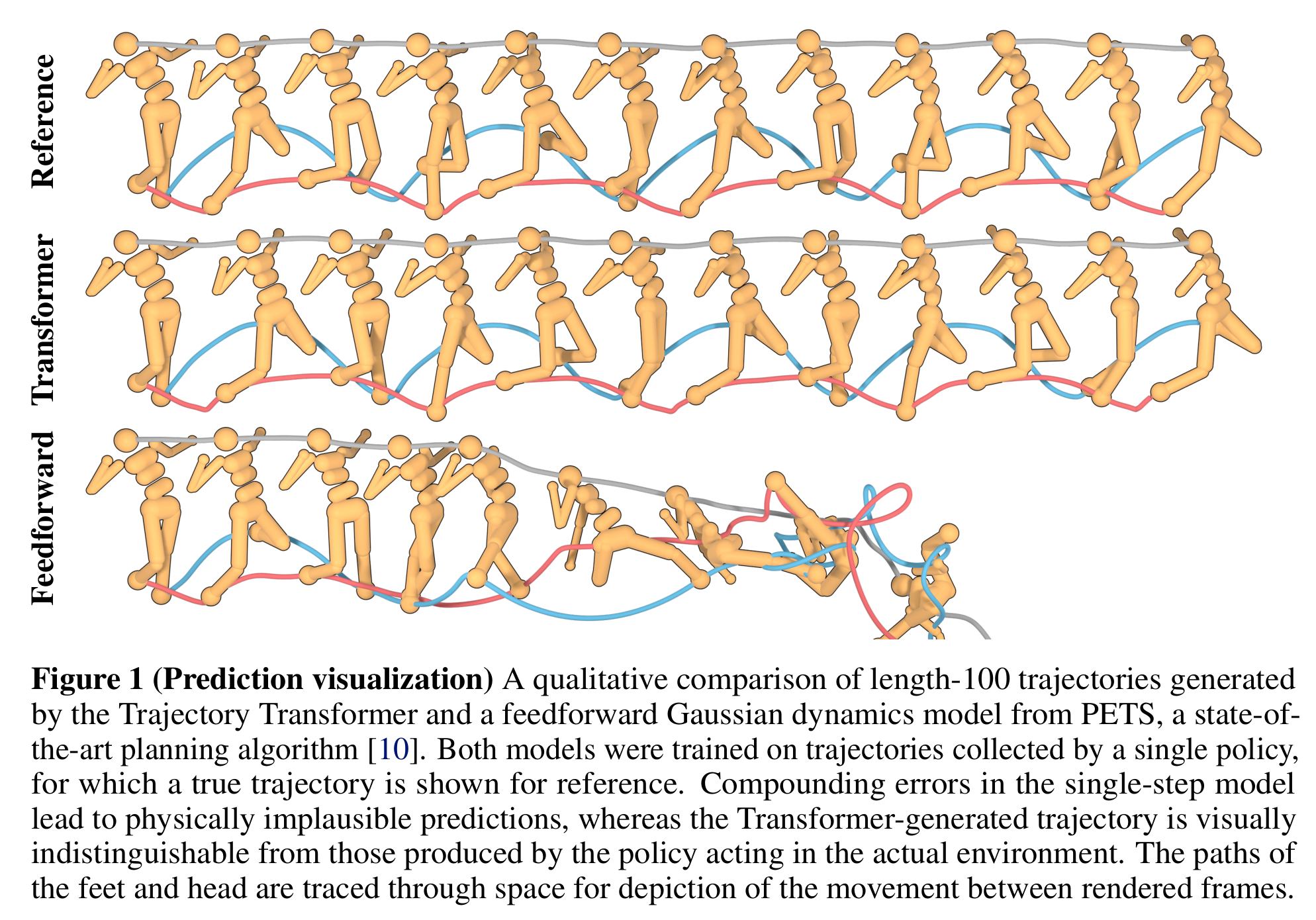
우선 long horizon predictive test에서는 좋은 성능을 보여주었다. Humanoid reference trajectory와 비교해서 Trajectory Transformer가 planning을 잘 해주고 있음을 볼 수 있다.

논문에서는 Markovian Transformer라는 구조와도 ablation study를 하는데 이 구조는 Trajectory Transformer가 직전 한 step만 볼 수 있도록 나머지는 모두 masking해주는 것이다.

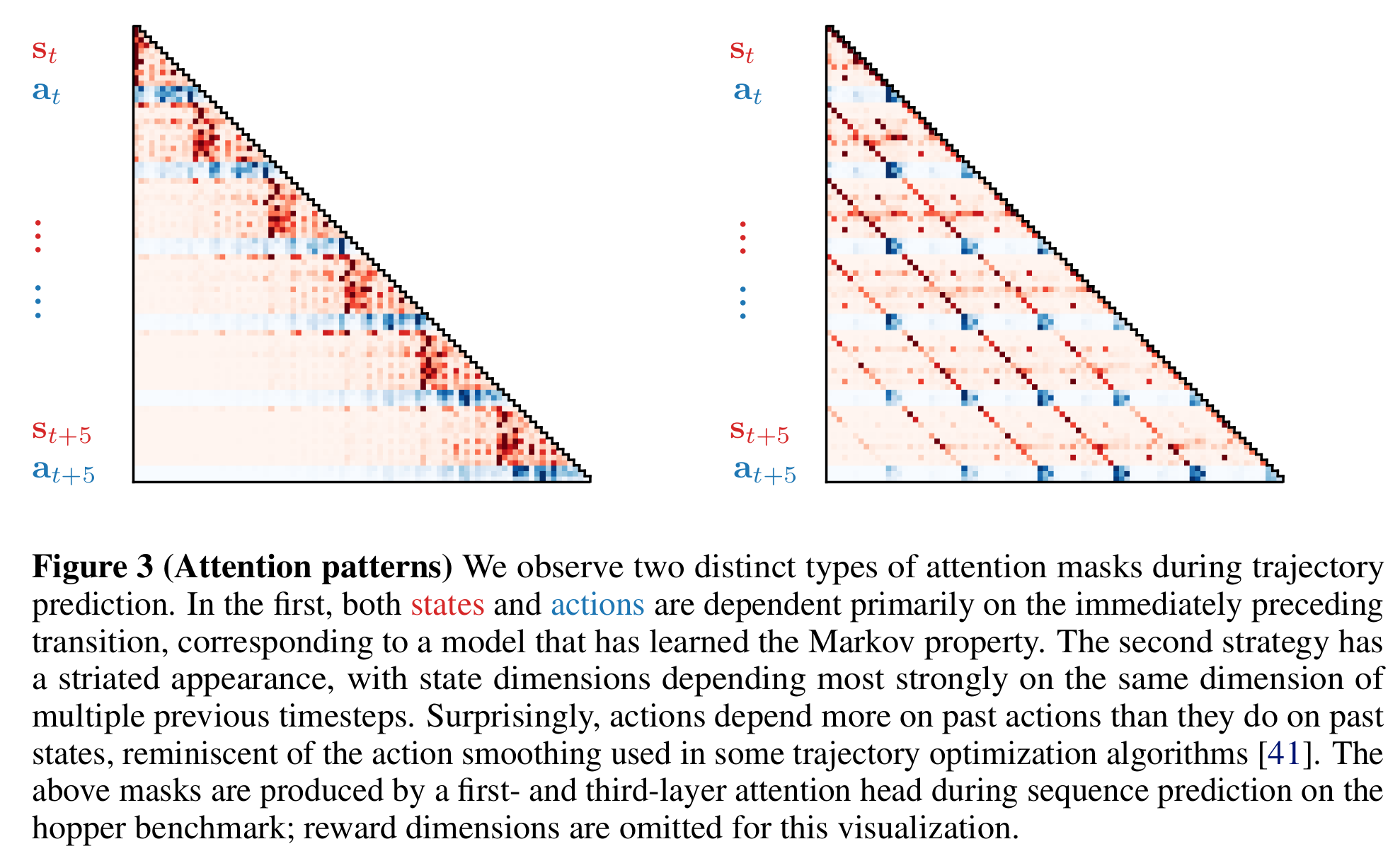
Attention pattern에 대해서도 언급하는데 다음과 같은 두 가지 재미있는 attention pattern이 나왔다고 한다.

Figure 3는 self-attention 구조 중 두 가지 attention block에서의 attention mask패턴인데 오니쪽은 Markov property를 학습한 것으로 해석할 수 있다. Attention이 모두 직전 상태와 행동에 강하게 집중되는 것을 볼 수 있다. 두 번째 재미있는 패턴은 action을 결정할 때 이전 상태보다 이전에 선택한 action들에 attention이 강하게 들어갔다는 점이다. 위 그림은 hopper benchmark에서 추출한 것이며 reward는 생략되었다.

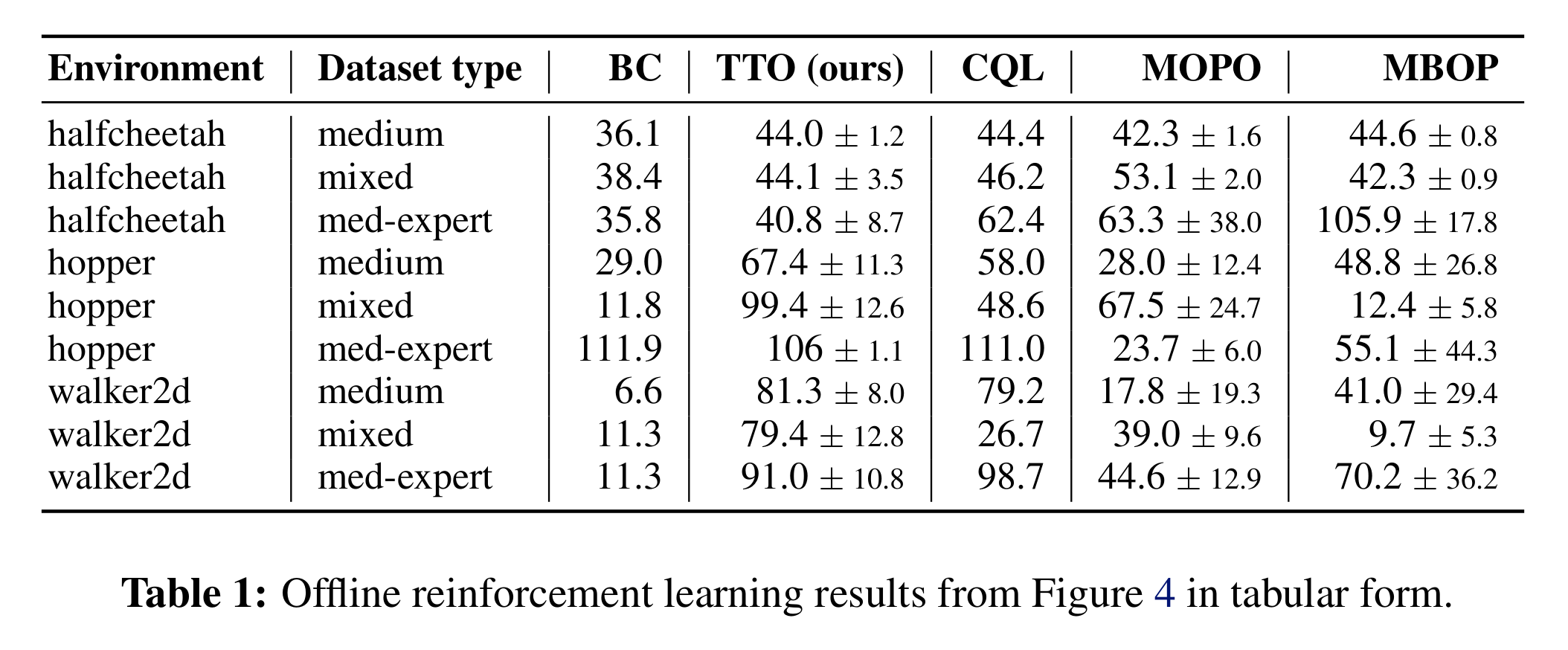
Offline RL의 benchmark도 보면 기존 offline RL방법들에 비견할만한 점수를 보여주고 있다.

Discussion

이 논문에서는 sequence modeling의 도구를 사용해 imitation learning, goal-reaching, offline reinforcement learning task를 수행할 수 있음을 부여주었다. 일반적인 online RL의 문제가 아니라 offline RL에의 적용이지만 기존 강화학습 framework으로 풀던 문제를 sequence modeling의 framework으로 접근해 유의한 성능을 거두었다는데 의의가 있다. Sequence model에서 Transformer architecture가 거두고 있는 상당한 성과를 볼 때 상당히 기대되는 접근방법이기도 하다. 저자는 TTO가 그동안 강화학습에서 Markov property와 같이 기본적으로 전제했던 가정들을 사용하지 않고도 offline RL에서 경쟁력있는 결과를 얻었다는 점을 강조하며 논문을 마무리한다.

Bibliography

Janner, Michael, Qiyang Li, and Sergey Levine. “Reinforcement Learning as One Big Sequence Modeling Problem.” arXiv preprint arXiv:2106.02039 (2021).

Reference

• An Optimistic Perspective on Offline Reinforcement Learning