Pitfalls of In-domain Uncertainty Estimation and Ensembling in Deep Learning

이 논문에서는 in-domain uncertainty estimation에서 현재 사용하는 metric들이 가지는 맹점들에 대해 다루고 다양한 ensembling techniques을 통해 얻은 deep ensemble equivalent score (DEE)라는 metric을 제시한다.

Abstract

논문에서 관심있는 대상은 in-domain uncertainty estimataion의 metric에 대한 것으로 특히 image 분류 문제이 있어 현재 사용되는 불확실성에 대한 정량화 방법과 metric이 가지는 맹점을 언급하며 Deep ensemble equivalent (DEE)라는 score를 제시한다. 그리고 복잡한 ensemble technique들도 몇 개의 독립적으로 훈련된 network의 ensemble 모델과 성능측면에서 동일함을 보인다.

Introduction

일반적으로 불확실성 측면에서 우리가 모델에게 기대하는 바는 OOD(out-of-domain) 데이터에 대해서는 in-domain 데이터보다 더 높은 불확실성을 갖기를 바란다. 딥러닝 모델이 잘못된 예측에 대해서 지나치게 높은 confidence 가지지 않도록 모델로 하여금 domain에 대한 이해를 시키는 것은 중요한 문제이다. 저자는 이러한 관점에서 metric과 ensemble 방법에 대해 유의할 점들을 소개한다.

Pitfalls of metrics

저자는 이 논문에서 in-domain에서 사용되는 uncertainty estimation metric (log-likelihood, Brier score, calibration metrics, etc.)이 다른 모델간에 직접 비교가 어렵다는 것을 보인다. 그리고 이러한 성질로 인해 모델의 uncertainty estimation 성능에 대한 ranking을 만드는 것이 어렵기 때문에 보다 합리적인 evaluation scheme을 제시한다고 한다. 예로 temperature scaling은 모델간 공정한 비교를 위해서 필수적이라는 것을 보인다던지 calibrated log-likelihood는 이 논문에서 지적하는 많은 in-domain uncertainty estimation task의 맹점을 피할 수 있는 metric임을 보이는 것이 이에 해당한다.

Pitfalls of ensembles

논문의 main contribution 중 하나는 deep ensemble equivalent (DEE)라는 measure를 제시하는 것이다. 이 지표는 ensemble 시켰을 때 동일한 성능을 얻기 위해서는 몇 개의 모델이 필요한지를 측정한다. DEE를 사용하게되면 다른 metric에서는 어려웠던 다른 dataset 혹은 architecture를 사용한 ensemble 방법에 대해서도 동일한 scale에서 비교할 수 있다는 장점이 있다.

Missing part of ensembling

저자는 test-time data augmentation (TTA) 기법이 uncertainty estimation에서 매우 효과적이었음을 확인하였다고 한다. 이 방법은 large-scale classification에서 자주 사용되는 방법인데 uncertainty estimation과 ensembling에서도 매우 효과적임을 보여준다.

Scope of the Paper

이 section에서는 논문에서 사용한 방식이 in-domain uncertainty에 대해서만 측정할 수 있도록 최대한 다른 기법은 자제하고 표준적인 방법을 사용했음을 밝힌다. 최적화나 ensemble 방법에 있어서도 훈련을 가속하고 더 나은 성능을 제공하는 방법이 있지만 최대한 raw power of ensembling techniques을 측정하기 위해 다른 방법들은 지양했다고 한다.

Pitfalls of In-domain Uncertainty Estimation

여기서는 Brier score, log-likelihood 등의 metric들이 어떤 맹점이 있는지, 그리고 이 맹점들로 인해 evaluation이 크게 달라질 수 있음을 보인다.

Log-likelihood and Brier Score

In-domain uncertainty를 확인하는 방법으로 가장 많이 사용되는 지표 중 하나는 average test log-likelihood이다.

$$ \mathrm{LL}=\frac{1}{n} \sum_{i=1}^{n} \log \hat{p}\left(y=y_{i}^{*} \mid x_{i}\right) $$

LL은 틀린 label에 높은 proability score가 부여되었을 때 또는 정답 label에 낮은 probability score가 부여되었을 때 penalize하는 지표이다. 문제는 LL이 softmax temperature $T$에 매우 예민하다는 것이다. 참고로 여기서 softmax는 일반적인 분류문제에서 neural network의 마지막 activation으로써의 softmax이며 $T$는 보통 훈련중에는 $T=1$로 고정된 값을 사용하거나 validation set에 대해 tuning되는 값이다.

$$\hat{p}(y \mid x) = \operatorname{Softmax}(z(x) / T)$$

이 때 $T$는 학습중에 implicit하게 학습되므로 test data에 대해 최적의 temperature라고 볼 수 없다. 하지만 최적의 temperature는 validation data에 대해 log-likelihood를 가장 크게 하는 값으로 찾을 수 있으며 이렇게 찾은 $T$를 사용하는 방식을 temperature scaling 또는 calibration이라고 한다. 단순한 방법이지만 temperature scaling은 LL을 사용할 때 상당한 성능향상을 보여준다. 저자가 문제로 삼는 부분 중 하나는 대부분의 경우(in practice) LL의 비교가 suboptimal temperature에서 이루어지고 있으며 이는 방법들 간의 성능에 대한 순위가 임의로 결정될 수 있는 여지를 만든다고 한다. 저자가 주장하는 바는 다음과 같다.

Comparison of the log-likelihood should only be performed at the optimal temperature.

실험적으로 calibrated log-likelihood를 사용하였을 때와 그렇지 않을 때의 차이는 다음과 같이 확인할 수 있었다고 한다.

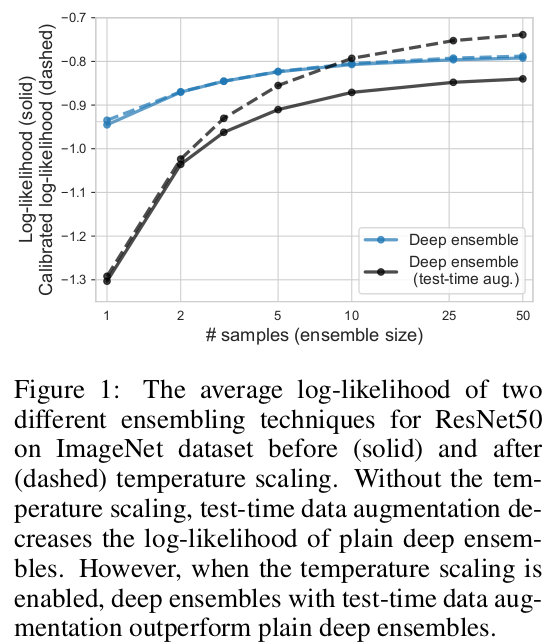
그래프를 보면 실선은 suboptimal temperature일 수 있는 LL, 점선은 optimal temperature를 적용한 LL이다. Temperature scaling을 하지 않은 경우 test-time augmentation에 대해서 성능이 하락하지만 temperature scaling을 해줄 경우 test-time data augmentation을 하면 plain deep ensemble을 넘어서는 성능을 보여주게 된다.

Brier score도 전반적으로 LL과 비슷한 성질을 가지며 마찬가지로 temperature에 예민하게 반응하므로 optimal temperature에서 비교해야한다고 말한다.

Misclassification Detection

보통 이진분류 문제에서 가장 많이 사용하는 지표는 AUC-ROC 또는 AUC-PR과 같은 지표이다. 하지만 이러한 지표들은 하나의 모델을 평가하는데는 적절하지만, 다른 모델들간의 misclassification performance를 비교하는 용도로 사용될 수 없다고 주장한다. 분류하는 task가 model-specific한 task이기 때문에 각가의 모델들은 고유의 이진분류 문제를 푸는 것으로 보아야 한다고 말한다. 저자는 다른 모델들 간에 이와 같은 지표를 사용하는 것은 본질적으로 다른 분류문제를 푸는 모델들의 성능을 같은 잣대로 비교하는 것이라고 말한다.

AUCs for misclassification detection cannot be directly compared between different models.

하지만 AUC기반의 평가가 uncertainty estimation에서 무조건 틀렸다고 말하는 것은 아니다. OOD detection의 경우 OOD data를 구분하는 것은 모든 모델들에게 동일하게 적용되는 것이므로 OOD detection에서는 유효하다고 언급한다.

Classification with Rejection

Misclassification detction에서 사용되는 accuracy-confidence curve라는 measure도 있는데 이는 특정 threshold $\tau$보다 큰 confidence $\max_{c} \hat{p}(y = c \mid x_{i})$의 accuracy만 측정하고 나머지는 무시하거나 reject하는 방법이다.

이 방법의 문제 역시 confidence를 결정하는 부분에서 calibration에 지나치게 의존한다는 점이다. 따라서 모델간의 temperature가 다르다면 confidence도 영향을 받아 의미있는 비교가 어렵다고 한다. 저자가 대안으로 제시하는 것은 thresholding을 confidence level로 하는 것이 아니라 rejected object의 숫자로 하는 것이다. Confidence를 threshold로 사용하게 되면 rejected object가 모델마다 달라지게 될텐데 애초에 threshold를 rejected object의 수로 맞추어주면 다른 모델끼리 비교할 때 모두 동일한 rejected object를 가진 상태를 갖게 되므로 비교가 용이하고 temperature scaling에도 상대적으로 덜 예민해진다고 한다. 이러한 curve를 accuracy-rejection curve라고 하며 비교를 쉽게 하기 위해 이 curve의 아래 면적인 AU-ARC를 사용할 것을 제안한다.

Calibration Metrics

Calibration metric인 ECE(Expected Calibaration Metric)과 TACE(Threshold Adaptive Calibration Error)를 소개하고 이들의 한계점에 대해 언급한다.

ECE는 probability score를 binning해서 해당 bin의 평균 accuracy와 비교하는 방법으로 miscalibration을 측정한다. $B_{m}$을 $m$번째 bin, $M$을 전체 bin의 개수라고 할 때 ECE는 다음과 같이 정의된다.

$$\tag{1} \mathrm{ECE}=\sum^{M} \frac{\left|B_{m}\right|}{n}\left|\operatorname{acc}\left(B_{m}\right)-\operatorname{conf}\left(B_{m}\right)\right| $$

이 때, $\operatorname{acc}(B) = \lVert B \rVert^{-1} \sum_{i \in B} \mathbb{I} [\argmax_{c} \hat{p}_{i, c} = y_{i}^{*}]$이고 $\operatorname{conf}(B) = \lVert B \rVert^{-1} \sum_{i \in B} \hat{p}_{i, y_{i}^{*}}$

acc는 각각의 bin 안에서 가장 높은 확률을 가진 class가 correct label과 일치하는 경우의 평균이며 conf는 정답 label에 대한 예측확률의 평균이다. 따라서 예측이 정확할 수록 ECE는 0에 가까워지는 성질을 갖게 된다.

하지만 calibration measuring 측면에서 최근에 다양한 문제가 제기되었다. Biased estimate이라는점, 직접 최적화할 수 없다는 점, 최대확률을 부여한 class에 대해서만 반영되고 다른 class는 반영하지 않는다는 점, 다른 모델간에 compatible하지 않는다는 점이 이에 해당한다.

이러한 단점을 일부 해결한 TACE가 제시되었다.

$$\tag{2} \mathrm{TACE}=\frac{1}{C M} \sum_{c=1}^{C} \sum_{m=1}^{M} \frac{\left|B_{m}^{\mathrm{TA}}\right|}{n}\left|\operatorname{objs}\left(B_{m}^{\mathrm{TA}}, c\right)-\operatorname{conf}\left(B_{m}^{\mathrm{TA}}, c\right)\right| $$

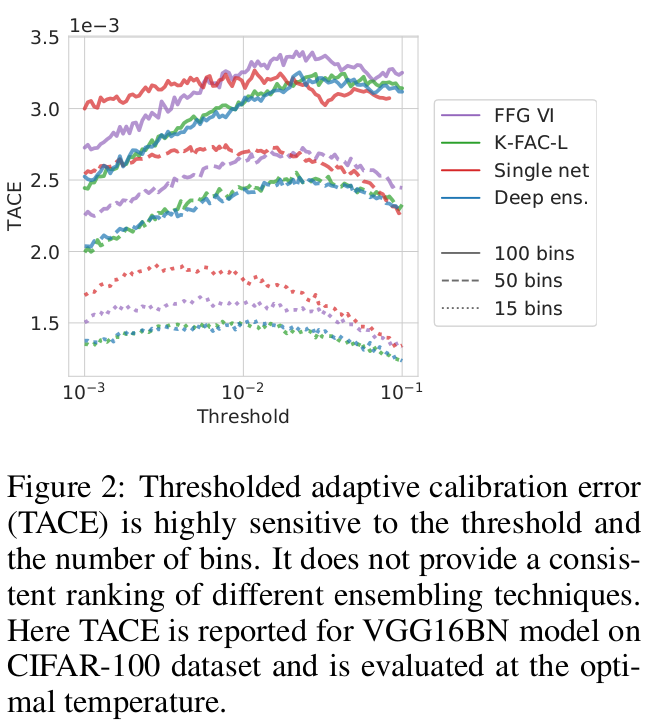
앞서 ECE가 최대확률이 부여된 class만 고려하는 점을 모든 class에 대해 고려하도록 개선하였으나 TACE 역시 모델마다 고유의 bias를 가지면서 biased estimate이라는 점에서 ECE의 문제를 모두 해결하지 못하였으며 특히 bin의 개수와 threshold에 따라 크게 바뀌는 값으로 모델을 비교하는데 있어 일관성 있는 지표로 사용하기 어렵다는 점을 지적한다.

Figure 2를 보면 bin의 개수와 threshold가 바뀜에 따라 TACE 기준으로 모델의 성능이 달라지는 것을 볼 수 있다.

Calibrated Log-likelihood and Test-time Cross-validation

Temperature scaling을 하는 방법은 크게 두 가지가 있다. Validation set을 이용해 temperature scaling을 하므로 training set에서 일부를 떼어내 validation으로 사용하거나 test set에서 validation으로 사용할 일부를 떼어내는 방법이 있다. Training set에서 떼어내면 발생하는 문제는 full training set을 활용할 수 없게 되어 모델을 직접 비교할 수 없다는 것이며 test set에서 떼어낼 경우 unbaised estimate이기는 하지만 variance가 더 커진다는 문제가 있다.

논문에서는 일단 test set에서 validation을 떼어내는 방식을 사용하며 variance를 줄이기 위해서 test-time cross-validation이라는 방식을 사용한다. 이 방법은 test set을 동일한 크기의 두 set으로 쪼갠 뒤 하나의 set을 사용해서 temperature를 찾고 다른 set에 이 temperature를 적용해 계산하는 방식이다. 이를 다섯번 수행해 평균을 냄으로써 variance를 줄여주게 된다.

A Study of Ensembling & Deep Ensemble Equivalent

저자는 deep neural network를 사용한 ensemble 학습이 크게 stochasatic computation graph와 snapshot-based methods 두 개의 paradigm으로 구분된다고 말한다. Stochastic computation graph는 weight이나 activation에 noise를 주는 방식으로 dropout, variational inference, batch normalization, Laplace approximation이 이 paradigm에 속한다고 말한다. 한편, snapshot-based method는 deep learning 모델로 부터 weights set을 얻고 prediction을 이 weight에 대해 평균을 계산한다. 이 논문에서는 deep ensembles (Lakshminarayanan et al., 2017)을 기반으로 ensemble method를 평가하는 방법을 제시한다.

저자는 deep ensemble equivalent (DEE) score라는 개념을 제시한다. 이 score는 ensembling technique의 성능을 측정하기 위해 deep ensemble 모델을 이용하는 방법이다.

What size of deep ensemble yields the same performance as a particular ensembling method?

즉 ensembling method를 평가하기 위해 동일 성능을 내기 위해서는 어느정도 크기의 deep ensemble이 필요한지를 기준으로 삼는 방식이다. Deep ensemble을 baseline으로 삼는 이유는 다른 ensembling technique과는 다르게 다른 mode를 갖는 loss landscape에 대해 독립적인 component 구성을 할 수 있다는 측면에서 직관적으로 더 좋은 결과를 제공하기 때문이라고 말한다. 저자가 여기서 말하고자 하는 바가 정확하게 와 닿지는 않지만 개인적으로 일반 ensemble의 경우 loss의 공간에서 특정 mode에 bound되어 다양한 결과를 얻기 힘든 반면 deep ensemble의 경우 mode측면에서 덜 bound되어 있어 uncertainty 추정 측면에 더 적합하다고 받아들이고 있다.

DEE는 ensembling method $m$에 대해 다음과 같이 구할 수 있다.

$$\tag{4} \operatorname{DEE}_{m}(k)= \min \left\lbrace l \in \mathbb{R}, l \geq 1 \mid \operatorname{CLL}_{D E}^{\operatorname{mean}}(l) \geq \mathrm{CLL}_{m}^{\operatorname{mean}}(k)\right\rbrace $$

Ensembling method $m$의 calibrated log-likelihood (CLL)보다 높은 CLL을 얻기 위해서 필요한 최소의 deep ensemble의 크기 $l$로 정의된다.

Figure 3는 여러 ensembling method에 대한 DEE를 보여준다. DEE 자체가 동일 성능에 필요한 최소한의 independently trained networks이므로 자연수로 표기된다.

추가로, test-time data augmentation이라는 방법을 언급하는데 이 방법은 대부분의 ensembling method에 대해 유의한 성능향상을 가져왔다고 말하고 있다.

원리는 매우 간단하다. Test-time에서 사용하는 이미지를 다양하게 augmentation을 적용하여 (여기서는 crop) ensemble model에 통과시키고 최종적으로 나온 prediction에 평균을 취해 가장 높은 값을 갖는 label을 최종예측으로 하는 것이다. Test-time data augmentation은 이미 최적화한 optimal temperature를 꼭 따르지는 않다보니 반드시 성능향상으로 연결되는 것은 아니다. 하지만 다양한 ensemble 모델에 적용하였을 때 test-time data augmentation을 적용한 결과가 더 좋은 CLL을 보여주었다고 한다.

Discussion & Conclusion

이 논문은 in-domain uncertainty estimation에 집중해 현재 사용되고 있는 metric들이 가지고 있는 한계점을 제시하고 DEE라는 ensemble 모델의 평가에 사용할 수 있는 score를 제시하였다. 또한 test-time data augmentation을 in-domain uncertainty estimation에 적용할 경우 효과적이라는 사실을 확인하였다. 저자는 uncertainty estimation field에서 다른 방법과 공정하게 비교할 수 있도록 신뢰할 수 있는 benchmark를 사용할 것을 촉구하며 논문을 맺는다.

Bibliography

Ashukha, Arsenii, et al. “Pitfalls of in-domain uncertainty estimation and ensembling in deep learning.” arXiv preprint arXiv:2002.06470 (2020).