3.8 Orthogonal Projections

머신러닝에서 다루는 데이터는 대부분 3차원 이상의 고차원데이터로, 사람이 인지할 수 있는 3차원이하의 공간으로는 데이터를 표현하기 어렵다는 문제가 있다. 하지만 데이터의 모든 정보가 중요한 경우는 많지 않다. 따라서, 필요없는 변수는 줄이고 가능한 한 중요한 정보만을 보존하는 변수를 활용하면 고차원의 데이터를 시각화가 가능한 영역까지 축소할 수 있다. 그렇다면 compression loss를 최소화하면서 중요한 정보를 보존하려면 어떻게 해야할까? 이러한 논의를 하기 위해 기초가 되는 projection에 대해 알아보자.
Projection
Projection의 정의는 다음과 같다.
직관적으로 생각해보면 projection은 벡터공간에서 특정 벡터공간으로의 함수이므로 이미 특정공간으로 projection하였다면 이에 대해 projection을 다시 하더라도 원래 projection과 결과가 같다.
Linear mapping은 transformation matrix로 표현할 수 있으므로 projection은 transformation matrix의 특별한 경우라고 할 수 있다. 선형변환을 표현하는 transformation matrix로 이 성질은 다음과 같이 쓸 수 있다.
$$ \boldsymbol{P}_{\pi}^2 = \boldsymbol{P}_{\pi} $$
이제부터 벡터의 orthogonal projection을 inner product space ($\mathbb{R}^n, \langle \cdot, \cdot \rangle$)에서 벡터부분공간의 함수로 다루게 된다. 거창하게 표현되었지만 쉽게 표현하면 $n$차원 데이터와 내적이 정의된 공간을 벡터부분공간으로 보내는 함수에 관한 내용이다. 아래의 projection 내용을 다룰 때 별도의 언급이 없는 한 내적은 dot product $\langle \boldsymbol{x}, \boldsymbol{y} \rangle = \boldsymbol{x}^\top \boldsymbol{y}$라고 가정한다.
Projection onto One-Dimensional Subspaces (Lines)
원점을 지나는 basis vector $\boldsymbol{b} \in \mathbb{R}^n$가 있을 때 $\operatorname{span}(\boldsymbol{b})$인 직선은 1차원 부분공간 $U \subseteq \mathbb{R}^n$로 나타낼 수 있다. $n$차원 공간의 임의의 벡터 $\boldsymbol{x} \in \mathbb{R}^n$를 직선으로 표현된 부분공간 $U$로 projection하려면 $U$공간에 있되, 가장 $\boldsymbol{x}$와 가까운 $\pi_{U}(\boldsymbol{x}) \in U$를 찾으면 된다. 이 때 $\pi_{U}(\boldsymbol{x})$의 성질은 다음과 같다.
-
$\pi_{U}(\boldsymbol{x})$는 $\boldsymbol{x}$와 가장 가까우며, 여기서 “가깝다"는 것은 $\lVert \boldsymbol{x} - \pi_{U}(\boldsymbol{x}) \rVert$가 가장 작을 때를 의미한다. 다시 말해, Euclidean 공간에서 $\boldsymbol{x}$을 $\operatorname{span}(\boldsymbol{b})$에 수직선을 내렸을 때의 거리이다. 이는 다음과 동치이다.
$$ \langle \pi_{U}(\boldsymbol{x}) - \boldsymbol{x}, \boldsymbol{b} \rangle = 0 $$
-
$\boldsymbol{x}$의 $U$위로의 projection $\pi_{U}(\boldsymbol{x})$은 $U$공간의 원소이며 따라서 basis vector $\boldsymbol{b}$의 스칼라곱으로 표현할 수 있다.
$$\pi_{U}(\boldsymbol{x}) = \lambda \boldsymbol{b}, \ \text{for some } \lambda \in \mathbb{R}$$
다음의 과정을 통해 $\boldsymbol{x} \in \mathbb{R}^n$를 $U$로 projection하는 $\lambda, \pi_{U}(\boldsymbol{x}) \in U, \boldsymbol{P}_{\pi}$를 유도할 수 있다.
1. Finding the coordinate $\lambda$
Orthogonality 정의에 의해 다음이 성립한다. $$\langle \boldsymbol{x} - \pi_{U}(\boldsymbol{x}), \boldsymbol{b} \rangle = 0 \overset{\pi_{U}(\boldsymbol{x}) = \lambda \boldsymbol{b}}{\iff} \langle \boldsymbol{x} - \lambda \boldsymbol{b}, \boldsymbol{b} \rangle = 0$$ 내적의 선형성을 이용하면 다음과 같이 쓸 수 있다. $$\langle \boldsymbol{x}, \boldsymbol{b} \rangle - \lambda \langle \boldsymbol{b}, \boldsymbol{b} \rangle = 0 \iff \lambda = \frac{\langle \boldsymbol{x}, \boldsymbol{b} \rangle}{\langle \boldsymbol{b}, \boldsymbol{b} \rangle} = \frac{\langle \boldsymbol{b}, \boldsymbol{x} \rangle}{\lVert \boldsymbol{b} \rVert^2}$$
만약 $\lVert \boldsymbol{b} \rVert = 1$이면 $\lambda$는 단순하게 $\boldsymbol{b}^T \boldsymbol{x}$을 계산함으로써 얻을 수 있다.
2. Finding the projection point $\pi_{U}(\boldsymbol{x}) \in U$
$\pi_{U}(\boldsymbol{x}) = \lambda \boldsymbol{b}$이므로
$$\pi_{U}(\boldsymbol{x}) = \lambda \boldsymbol{b} = \frac{\langle \boldsymbol{b}, \boldsymbol{x} \rangle}{\lVert \boldsymbol{b} \rVert^2} \boldsymbol{b} = \frac{\boldsymbol{b}^\top \boldsymbol{x}}{\lVert \boldsymbol{b} \rVert^2} \boldsymbol{b}$$
Projection의 길이는 다음과 같다.
$$\lVert \pi_{U}(\boldsymbol{x}) \rVert = \lVert \lambda \boldsymbol{b} \rVert = \lvert \lambda \rvert \lVert \boldsymbol{b} \rVert$$
나아가, dot product에 대해서는 다음의 관계까지도 성립한다.
$$\lVert \pi_{U}(\boldsymbol{x}) \rVert = \lvert \cos \omega \rvert \lVert \boldsymbol{x} \rVert$$
3. Finding the projection matrix $\boldsymbol{P}_{\pi}$
Projection matrix $\boldsymbol{P}_{\pi}$가존재할 때 projection은 다음과 같이 표현된다.
$$\pi_{U}(\boldsymbol{x}) = \boldsymbol{P}_{\pi}\boldsymbol{x}$$
위의 유도를 이용하면,
$$\pi_{U}(\boldsymbol{x}) = \lambda \boldsymbol{b} = \boldsymbol{b}\lambda = \boldsymbol{b} \frac{\boldsymbol{b}^\top \boldsymbol{x}}{\lVert \boldsymbol{b} \rVert^2} = \frac{\boldsymbol{b}\boldsymbol{b}^\top}{\lVert \boldsymbol{b} \rVert^2} \boldsymbol{x}$$
로부터
$$\boldsymbol{P}_{\pi} = \frac{\boldsymbol{b}\boldsymbol{b}^\top}{\lVert \boldsymbol{b} \rVert^2}$$
임을 알 수 있다. $\boldsymbol{P}_{\pi}$는 rank 1의 symmetric matrix이며 $\lVert \boldsymbol{b} \rVert^{2} = \langle \boldsymbol{b}, \boldsymbol{b} \rangle$임에 유의하자.
이 과정을 통해 얻은 projection matrix $\boldsymbol{P}_{\pi}$는 공간 내 임의의 벡터 $\boldsymbol{x} \in \mathbb{R}^{n}$을 원점을 지나는 벡터 $\boldsymbol{b}$의 직선으로 projection하는 변환행렬이 된다.
Example
원점을 지나고 벡터 $\boldsymbol{b} = \begin{bmatrix}1 & 2 & 2 \end{bmatrix}^{\top}$에 의해 span되는 직선으로 projection시키는 projection matrix를 찾아보자. $\boldsymbol{b}$는 1차원 부분공간의 basis이다.
Projection matrix를 구하는 공식을 위에서 유도하였으므로 공식에 대입만 하면 된다. 대입하면 아래와 같은 행렬을 얻을 수 있다.
$$ \boldsymbol{P}_{\pi}=\frac{\boldsymbol{b} \boldsymbol{b}^{\top}}{\boldsymbol{b}^{\top} \boldsymbol{b}}=\frac{1}{9}\left[\begin{array}{l} 1 \cr 2 \cr 2 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 2 \end{array}\right]=\frac{1}{9}\left[\begin{array}{lll} 1 & 2 & 2 \cr 2 & 4 & 4 \cr 2 & 4 & 4 \end{array}\right] $$
실제로 $\begin{bmatrix}1 & 1 & 1\end{bmatrix}^{\top}$에 projection matrix를 적용해 $\boldsymbol{b}$ 위로 projection 되었는지 확인해보자.
$$ \pi_{U}(\boldsymbol{x})=\boldsymbol{P}_{\pi} \boldsymbol{x}=\frac{1}{9}\left[\begin{array}{lll} 1 & 2 & 2 \cr 2 & 4 & 4 \cr 2 & 4 & 4 \end{array}\right]\left[\begin{array}{l} 1 \cr 1 \cr 1 \end{array}\right]=\frac{1}{9}\left[\begin{array}{c} 5 \cr 10 \cr 10 \end{array}\right] \in \operatorname{span} \lbrack \left\lbrack \begin{array}{l} 1 \cr 2 \cr 2 \end{array} \right\rbrack \rbrack $$
또한, 이미 projection된 벡터에 대해 같은 projection matrix을 적용하면 달라지는 것이 없음도 확인할 수 있다. ($\boldsymbol{P}_{\pi}^{2} \boldsymbol{x} = \boldsymbol{P}_{\pi} \boldsymbol{x}$)
Projection onto General Subspaces
여기서는 직선에 국한되지 않고 일반공간으로의 projection에 대해 다룬다. 3차원 공간에서 2차원 평면으로의 projection, 혹은 그릴 수는 없지만 4차원 이상 공간에서 3차원으로의 projection 등이 이에 해당한다. 이에 따라 앞에서 예시로 삼았던 basis vector $\boldsymbol{b}$도 여러개의 basis vector가 되면서 행렬로 표현하게 된다.
Subspace $U$의 ordered basis가 $(\boldsymbol{b}_1, \ldots, \boldsymbol{b}_m)$이라고 할 때, $U$ 위로의 어떤 projection $\pi_{U}(\boldsymbol{x})$은 반드시 $U$의 원소여야 한다. 따라서 Projection은 $U$의 basis로 표현이 가능하다.
$$ \pi_{U}(\boldsymbol{x}) = \sum_{i=1}^{m} \lambda_i \boldsymbol{b}_{i} $$
앞에서 다룬 직선으로의 projection과 마찬가지로 세 가지 단계를 통해 $\boldsymbol{\lambda}$, $\pi_{U}(\boldsymbol{x})$와 projection matrix $\boldsymbol{P}_{\pi}$를 유도해보자.
1. Finding the coordinates $\lambda_1, \ldots, \lambda_m$
일반공간으로의 projection을 할 때는 basis가 여러 개이므로 행렬로 표현하면 projection은 다음과 같이 표현할 수 있다.
Basis행렬 $\boldsymbol{B}$을 다음과 같이 정의하자.
$$ \boldsymbol{B} = [\boldsymbol{b}_1, \ldots, \boldsymbol{b}_m] \in \mathbb{R}^{n \times m} $$
좌표를 나타내는 $\boldsymbol{\lambda}$는 다음과 같이 정의하자.
$$ \boldsymbol{\lambda} = [\lambda_1, \ldots, \lambda_m]^\top \in \mathbb{R}^m $$
이 때, projection의 선형결합은 다음처럼 쓸 수 있다.
$$ \pi_{U}(\boldsymbol{x}) = \sum_{i=1}^{m} \lambda_i \boldsymbol{b}_{i} = \boldsymbol{B\lambda} $$
차원은 늘어났지만 정의 자체는 변함이 없다. $\boldsymbol{x} \in \mathbb{R}^n$와 해당 벡터의 projection $\pi_{U}(\boldsymbol{x}) \in U$은 최단거리를 가져야하며 이는 $\boldsymbol{x} \in \mathbb{R}^n$와 $\pi_{U}(\boldsymbol{x}) \in U$를 잇는 벡터 $\boldsymbol{x} - \pi_{U} (\boldsymbol{x})$가 $U$의 모든 basis들과 직교할 때 성립한다. 따라서 $m$개의 basis가 있다면 모두에 대해 다음 조건을 만족해야 한다.
$$ \begin{aligned} \langle \boldsymbol{b}_1, \boldsymbol{x} - \pi_{U}(\boldsymbol{x}) \rangle &= \boldsymbol{b}_1^\top (\boldsymbol{x} - \pi_{U} (\boldsymbol{x})) = 0 \cr &\vdots \cr \langle \boldsymbol{b}_m, \boldsymbol{x} - \pi_{U}(\boldsymbol{x}) \rangle &= \boldsymbol{b}_m^\top (\boldsymbol{x} - \pi_{U} (\boldsymbol{x})) = 0 \end{aligned} $$
$\pi_{U}(\boldsymbol{x}) = \sum_{i=1}^{m} \lambda_i \boldsymbol{b}_{i} = \boldsymbol{B\lambda}$이므로 다음과 같이 쓸 수 있다.
$$ \begin{aligned} \boldsymbol{b}_1^\top (\boldsymbol{x} - &\boldsymbol{B}\boldsymbol{\lambda}) = 0 \cr \vdots \cr \boldsymbol{b}_m^\top (\boldsymbol{x} - &\boldsymbol{B}\boldsymbol{\lambda}) = 0 \end{aligned} $$
이를 다시쓰면 다음과 같은 homogeneous linear equation을 얻을 수 있다.
$$ \begin{bmatrix} \boldsymbol{b}_1^\top \cr \vdots \cr \boldsymbol{b}_m^\top \end{bmatrix} \begin{bmatrix} \boldsymbol{x} - \boldsymbol{B}\boldsymbol{\lambda} \end{bmatrix} = \boldsymbol{0} \iff \boldsymbol{B}^\top(\boldsymbol{x} - \boldsymbol{B}\boldsymbol{\lambda}) = \boldsymbol{0} $$
우항을 정리하면 다음이 된다.
$$ \boldsymbol{B}^\top \boldsymbol{B} \boldsymbol{\lambda} = \boldsymbol{B}^\top \boldsymbol{x} $$
그리고 이 식을 normal equation이라고 한다.
$\boldsymbol{B}$의 열벡터들이 ordered basis이므로 각각의 열벡터들은 선형독립이다. 따라서 $\boldsymbol{B}^\top \boldsymbol{B} \in \mathbb{R}^{m \times m}$은 regular하고 invertible하다. 따라서 $\boldsymbol{\lambda}$는 다음을 통해 얻을 수 있다.
$$ \boldsymbol{\lambda} = (\boldsymbol{B}^{\top} \boldsymbol{B})^{-1} \boldsymbol{B}^\top \boldsymbol{x} $$
이 때, $(\boldsymbol{B}^\top \boldsymbol{B})^{-1} \boldsymbol{B}^\top$를 $\boldsymbol{B}$의 pseudo-inverse라고 한다. $\boldsymbol{B}^\top \boldsymbol{B}$는 항상 square matrix형태이므로 $\boldsymbol{B}^\top \boldsymbol{B}$가 positive-definite하기만 하다면(즉 $\boldsymbol{B}$가 full-rank라면!) 이는 non-square matrix $\boldsymbol{B}$에 대해서도 적용가능하다. 다만 컴퓨터 연산시에 수치적 안정성때문에 $\boldsymbol{B}^\top \boldsymbol{B}$에 $\epsilon I$를 더해주기도 한다.
2. Finding the projection $\pi_{U}(\boldsymbol{x}) \in U$
앞에서 대부분의 내용을 다루어 $\pi_{U}(\boldsymbol{x})$를 구하는 것은 간단하다. $\pi_{U}(\boldsymbol{x}) = \boldsymbol{B} \boldsymbol {\lambda}$이므로 projection은 다음과 같이 구할 수 있다.
$$ \pi_{U}(\boldsymbol{x}) = \boldsymbol{B}(\boldsymbol{B}^\top \boldsymbol{B})^{-1} \boldsymbol{B}^\top \boldsymbol{x} $$
3. Finding the projection matrix $\boldsymbol{P}_{\pi}$
$\boldsymbol{P}_{\pi}\boldsymbol{x} = \pi_{U}(\boldsymbol{x})$로 부터 projection matrix는 위 식과 비교해 간단히 확인할 수 있다.
$$ \boldsymbol{P}_{\pi} = \boldsymbol{B}(\boldsymbol{B}^\top \boldsymbol{B})^{-1} \boldsymbol{B}^\top $$
앞에서 다룬 1차원은 위 식에서 $\boldsymbol{B}^\top \boldsymbol{B} \in \mathbb{R}$인 특수한 경우라고 볼 수 있다.
참고로 basis를 orthonormal basis로 구성하였다면 $\boldsymbol{B}^{\top}\boldsymbol{B} = \boldsymbol{I}$가 되어 역행렬계산을 할 필요가 없어진다.
Example
교재 예제 3.11에 해당하는 내용이다. 예제로 2차원 평면위로 projection하는 경우를 살펴보자. 벡터부분공간 $U$가 $U = \operatorname{span}[ \begin{bmatrix}1 \cr 1 \cr 1\end{bmatrix}, \begin{bmatrix}0 \cr 1\cr 2\end{bmatrix} ] \subseteq \mathbb{R}^{3}$이고 벡터 $\boldsymbol{x} = \begin{bmatrix}6 \cr 0 \cr 0\end{bmatrix} \in \mathbb{R}^{3}$일때 $\boldsymbol{x}$를 $U$로 projection한 좌표 $\boldsymbol{\lambda}$와 pojection point $\pi_{U}(\boldsymbol{x})$, projection matrix $\boldsymbol{P}_{\pi}$를 구해보자.
우선, 부분공간 $U$를 표현하는 generating set을 구해보자. 주어진 벡터가 이미 선형독립인 basis이므로 행렬 $\boldsymbol{B}$로 나타내면 다음과 같다.
$$\boldsymbol{B} = \begin{bmatrix}1 & 0\cr 1 & 1\cr 1 & 2\end{bmatrix}$$
위에서 구한 공식을 활용하기위해 필요한 $\boldsymbol{B}^{\top}\boldsymbol{B}$와 projection 벡터 $\boldsymbol{B}^{\top} \boldsymbol{x}$도 계산해두자.
$$ \begin{aligned} \boldsymbol{B}^{\top} \boldsymbol{B} &=\left[\begin{array}{lll} 1 & 1 & 1 \cr 0 & 1 & 2 \end{array}\right]\left[\begin{array}{ll} 1 & 0 \cr 1 & 1 \cr 1 & 2 \end{array}\right]\cr &=\left[\begin{array}{ll} 3 & 3 \cr 3 & 5 \end{array}\right] \end{aligned} $$$$ \begin{aligned} \boldsymbol{B}^{\top} \boldsymbol{x} &=\left[\begin{array}{lll} 1 & 1 & 1 \cr 0 & 1 & 2 \end{array}\right]\left[\begin{array}{l} 6 \cr 0 \cr 0 \end{array}\right]\cr &=\left[\begin{array}{l} 6 \cr 0 \end{array}\right] \end{aligned} $$
이제 normal equation인 $\boldsymbol{B}^{\top} \boldsymbol{B} \boldsymbol{\lambda} = \boldsymbol{B}^{\top} \boldsymbol{x}$를 통해 $\boldsymbol{\lambda}$를 계산하면 된다.
$$ \left[\begin{array}{ll} 3 & 3 \cr 3 & 5 \end{array}\right]\left[\begin{array}{l} \lambda_{1} \cr \lambda_{2} \end{array}\right]=\left[\begin{array}{l} 6 \cr 0 \end{array}\right] \Longleftrightarrow \boldsymbol{\lambda}=\left[\begin{array}{c} 5 \cr -3 \end{array}\right] $$
위의 좌표를 각 basis에 대한 선형결합으로 만들면 projection $\pi_{U}(\boldsymbol{x})$를 구할 수 있다.
$$ \begin{aligned} \pi_{U}(\boldsymbol{x}) &= 5 \begin{bmatrix}1 \cr 1 \cr 1\end{bmatrix} - 3 \begin{bmatrix}0 \cr 1\cr 2\end{bmatrix}\cr &= \begin{bmatrix}5 \cr 2 \cr -1\end{bmatrix} \end{aligned} $$
이 결과는 $\boldsymbol{B} \boldsymbol{\lambda}$와 같다.
벡터 $\boldsymbol{x}$와 $U$로 projection된 벡터의 크기차이는 $\boldsymbol{x} - \pi_{U}(\boldsymbol{x})$의 norm으로 계산할 수 있다.
$$ \lVert \boldsymbol{x}-\pi_{U}(\boldsymbol{x}) \rVert = \left\lVert \left[\begin{array}{lll} 1 & -2 & 1 \end{array} \right]^{\top} \right\rVert=\sqrt{6} $$
마지막으로, projection을 공식을 이용해 구하면 다음과 같다.
$$ \begin{aligned} \boldsymbol{P}_{\pi}&=\boldsymbol{B}\left(\boldsymbol{B}^{\top} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\top}\cr &=\frac{1}{6}\left[\begin{array}{ccc} 5 & 2 & -1 \cr 2 & 2 & 2 \cr -1 & 2 & 5 \end{array}\right] \end{aligned} $$
Relationship between Least-square Solution in Linear System
일반공간에서의 정의를 다시 한 번 살펴보며 정리해보자.
$$ \pi_{U}(\boldsymbol{x}) = \sum_{i=1}^{m} \lambda_i \boldsymbol{b}_i = \boldsymbol{B}\boldsymbol{\lambda} $$
여기서 $\pi_{U}(\boldsymbol{x})$는 $U$로의 projection이며 이 projection은 projection matrix $\boldsymbol{P}_{\pi}$가 벡터 $\boldsymbol{x}$를 Linear mapping함으로써 결정된다.
이를 상기하고 다음의 선형시스템을 보자.
$$ \boldsymbol{A} \boldsymbol{x} = \boldsymbol{b} $$
그리고 $\boldsymbol{b}$가 $\boldsymbol{A}$의 span위에 있지 않다면, 즉 $\boldsymbol{A}$의 column space의 span으로 표현되지 않는다면, 해 $\boldsymbol{x}$는 존재하지 않는다. 다만 우리는 projection을 이용해 $\boldsymbol{A}$에 속하는 벡터중에서 가장 $\boldsymbol{b}$에 가까운 approximate solution을 찾을 수 있다. 이 최소한의 오차를 가질때의 해 $\boldsymbol{x}$를 구하는 것이 바로 least-squares solution인 것이다.
Gram-Schmidt Orthogonalization
지금까지 basis가 주어졌을 때 projection을 하는 방법엔 대해 다루었다. 그렇다면 $n$-차원의 직교하지 않는 basis들이 주어졌을 때 어떻게 이들을 orthogonal/orthonormal하게 바꿀 수 있을까?
Gram-Schmidt orthogonalization 방법을 사용해서 반복적 계산을 통해 주어진 basis로부터 직교하는 basis집합을 구성할 수 있다.
계산 방법은 다음과 같다.
우선 Orthogonal basis set을 구성할 첫 번째 Basis를 선택한다.
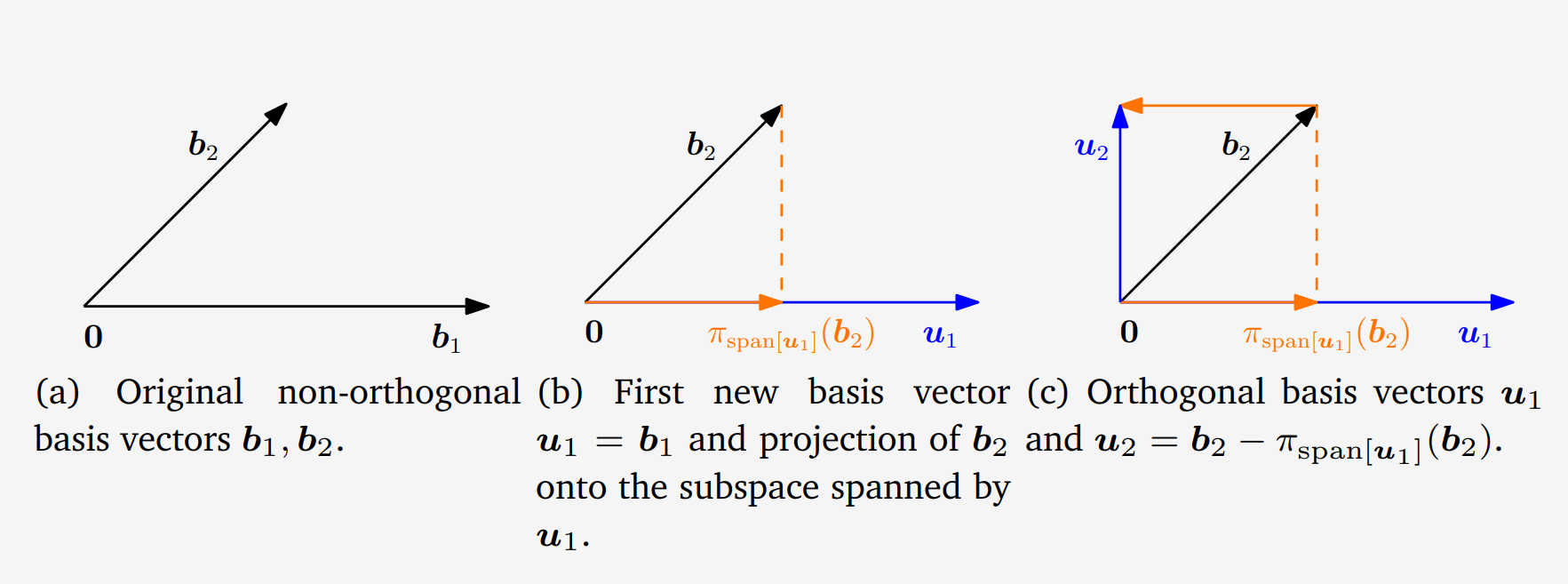
$$ \boldsymbol{u}_1 := \boldsymbol{b}_1 $$
첫번째 벡터를 기준으로 다음 계산을 통해 $\boldsymbol{b}_1$에 직교하는 벡터 $\boldsymbol{u}_2$를 얻을 수 있다.
$$ \boldsymbol{u}_2 := \boldsymbol{b}_2 - \pi_{\operatorname{span}[\boldsymbol{u}_1]}(\boldsymbol{b_2}) $$
위 식을 살펴보면 두번째 basis를 $\boldsymbol{u}_1$으로 projection하고 이 둘을 잇는 벡터 $\boldsymbol{u}_{2}$를 만든다는 것을 알 수 있다.
교재 Fig 3.12에서 이를 잘 보여준다.
세번째 basis가 있다면 다음과 같이 구한다.
$$ \boldsymbol{u}_3 := \boldsymbol{b}_3 - \pi_{\operatorname{span}[\boldsymbol{u}_1]}(\boldsymbol{b_3}) - \pi_{\operatorname{span}[\boldsymbol{u}_2]}(\boldsymbol{b_3}) $$
이를 일반식으로 나타내면 다음과 같이 표현할 수 있다. 아래의 식을 통해 basis집합내의 모든 basis를 직교하게 만들 수 있다.
$$ \boldsymbol{u}_k := \boldsymbol{b}_k - \pi_{\operatorname{span}[\boldsymbol{u}_1, \ldots, \boldsymbol{u}_{k-1}]}(\boldsymbol{b_k}), \quad k = 2, \ldots, n $$
이와 같이, Gram-Schmidt orthogonalization을 통해 $n$개의 basis vector $(\boldsymbol{b}_1, \ldots, \boldsymbol{b}_n)$를 직교벡터 $(\boldsymbol{u}_1, \ldots, \boldsymbol{u}_n)$로 변환할 수 있다. 여기서 각각의 $\boldsymbol{u}_k$를 normalize하면 orthonormal basis set이 된다.
Example
다음 두 basis 벡터 $\boldsymbol{b}_1, \boldsymbol{b}_2 \in \mathbb{R}^2$를 Gram-Schmidt Orthogonalization을 이용해 직교하는 basis집합을 만들어 보자.
$$ \boldsymbol{b}_{1}=\left[\begin{array}{l} 2 \cr 0 \end{array}\right], \quad \boldsymbol{b}_{2}=\left[\begin{array}{l} 1 \cr 1 \end{array}\right] $$
앞서 언급한 절차에 따라 orthogonal basis를 구성해보자.
우선, 첫번째 basis vector를 설정하자.
$$ \boldsymbol{u}_{1}:=\boldsymbol{b}_{1}=\left[\begin{array}{l} 2 \cr 0 \end{array}\right] $$
이어서 $\boldsymbol{b}_2$와 $\boldsymbol{b}_2$를 $\boldsymbol{b}_1$위로 projection한 벡터를 잇는 벡터를 만들면 된다.
$$ \begin{aligned} \boldsymbol{u}_{2}&:=\boldsymbol{b}_{2}-\pi_{\mathrm{span}\left[\boldsymbol{u}_{1}\right]}\left(\boldsymbol{b}_{2}\right) \cr &= \boldsymbol{b}_{2}-\frac{\boldsymbol{u}_{1} \boldsymbol{u}_{1}^{\top}}{\lVert \boldsymbol{u}_{1} \rVert^{2}} \boldsymbol{b}_{2}\cr &=\left[\begin{array}{l} 1 \cr 1 \end{array}\right]-\left[\begin{array}{ll} 1 & 0 \cr 0 & 0 \end{array}\right]\left[\begin{array}{l} 1 \cr 1 \end{array}\right]\cr &=\left[\begin{array}{l} 0 \cr 1 \end{array}\right] \end{aligned} $$
Orthonormal basis set으로 구성하고 싶다면 구한 $\boldsymbol{u}_1, \boldsymbol{u}_2$를 normalize만 해주면 된다. 두 벡터의 내적은 0으로 직교함을 쉽게 확인할 수 있다.
Projection onto Affine Subspace
Affine 공간으로의 projection에 대해서도 알아보자. 앞서 affine 공간에 대해 다루었다. 매우 느슨하게 말하면 벡터부분공간을 어떤 벡터 $\boldsymbol{x}$만큼 이동시킨 공간이고 원점을 지나지 않는다는 특징이 있다.
예를 들어 어떤 affine 공간 $L$이 있고 이 공간은 basis vector $\boldsymbol{b}_1, \boldsymbol{b}_2$가 구성하는 벡터공간 $U$를 $\boldsymbol{x}_0$만큼 이동시킨 공간이라고 해보자.
$$L = \boldsymbol{x}_0 + U$$
임의의 벡터 $\boldsymbol{x}$를 공간 $L$로 projection하는 $\pi_{L}(\boldsymbol{x})$를 구하는 것이 목적이다.구하는 방법은 직관적으로도 쉽게 이해할 수 있다. Affine 공간이 벡터부분공간 $U$를 $\boldsymbol{x}_0$만큼 이동시킨 것이므로, $L - \boldsymbol{x}_0$, 즉 $U$는 벡터부분공간이다. 따라서 앞에서 다룬 내용을 통해 벡터를 벡터부분공간 $U$로 projection하고 이를 $\boldsymbol{x}_0$만큼 이동시키면 문제가 간단히 해결된다.
따라서, $L$로의 projection은 다음 식을 통해 얻을 수 있다.
$$\pi_{L}(\boldsymbol{x}) = \boldsymbol{x}_0 + \pi_U (\boldsymbol{x} - \boldsymbol{x}_0)$$
또한, affine 공간 $L$위로의 projection과 원래 벡터 $\boldsymbol{x}$사이의 거리는 $\boldsymbol{x} - \boldsymbol{x}_0$와 $U$의 거리와 같아야 한다.
$$ \begin{aligned} d(\boldsymbol{x}, L) &=\lVert \boldsymbol{x}-\pi_{L}(\boldsymbol{x}) \rVert = \lVert \boldsymbol{x}-\left(\boldsymbol{x}_{0}+\pi_{U}\left(\boldsymbol{x}-\boldsymbol{x}_{0}\right)\right) \rVert \cr &=d\left(\boldsymbol{x}-\boldsymbol{x}_{0}, \pi_{U}\left(\boldsymbol{x}-\boldsymbol{x}_{0}\right)\right)=d\left(\boldsymbol{x}-\boldsymbol{x}_{0}, U\right) \end{aligned} $$