ODIN: Enhancing the Reliability of Out-of-distribution Image Detection in Neural Networks

딥러닝을 사용한 모델이 잘 분류하는 것과는 별개로 모델이 보는 image가 학습시 사용했던 분포(in-distribution)에서 왔는지, 학습 중에 보지 못했던 분포(out-of-distribution)에서 왔는지를 구별하는 것은 중요한 문제이다. ODIN은 기존 분류기를 그대로 사용하면서 간단하게 out-of-distribution을 구분하는 방법을 제시한다.

Abstract

ODIN(Out-of-distribution detector for neural networks)이라는 OOD(out-of-distribution)을 구분하는 방법을 제시한 논문으로 이 방법은 기존에 사용하는 pre-trained neural network를 수저하지 않고 그대로 사용할 수 있다는 게 큰 장점이다. OOD를 구분하기 위한 핵심 아이디어로 temeprature scaling과 input에 대한 perturbation을 이용한다. 간단하게 구현할 수 있는 방법이나 큰 폭의 성능 향상을 보인 방법이다.

Introduction

이 논문은 OOD detection 문제를 다루며 기본적으로 Hendrycks & Gimple의 A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks의 연장선에 있다. Hendrycks & Gimple은 해당 논문에서 잘 훈련된 neural network는 in-distribution sample에 대해 out-of-distribution sample 보다 더 높은 softmax score가 부여되는 성질을 이용하였다.

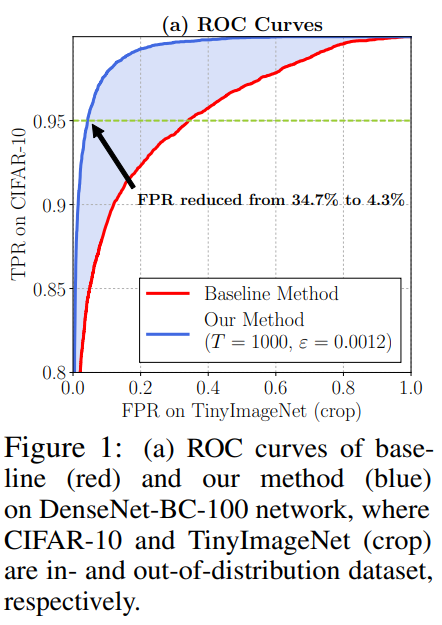
본 논문에서는 여기에 temperature scaling과 input에 small perturbation을 더해 in- and out-of-distribution의 softmax score 차이를 더 크게 만드는 방법을 제시한다. 실제로, 이 방법을 CIFAR-10 dataset(positive samples)을 사용해 훈련시킨 DenseNet에 OOD인 TinyImageNet dataset(negative samples)을 구분하는 task에 적용했을 때, 95% 확률로 in-distribution image를 구분할 수 있는 setting에서 false positive rate을 34.7%에서 4.3%로 대폭 개선한 결과를 보여준다.

Problem Statement

논문에서 다루고자 하는 문제는 in-distribution $P_{X}$와 out-distribution $Q_{X}$를 구분하는 것이다.

Can we distinguish whether the image is from in-distribution $P_{X}$ or not?

여기서는 OOD를 잘 구분하는 지에 집중한다. In-distribution에서 분류를 잘하는 것도 중요하지만 in-distribution을 맞게만 분류했다면 이미 사용하고 있는 pre-trained network로 inference하면 끝나는 일인지라 OOD detection에 대해서만 집중적으로 언급한다.

ODIN: Out-of-distribution Detector

앞서 언급한대로 ODIN의 핵심은 temperature scaling과 input에 perturbation을 주는 input preprocessing 두 가지이다. 각가을 살펴보자.

Temperature Scaling

$N$개의 class를 분류하는 network $\boldsymbol{f}$가 있다고 해보자. 어떤 input image $\boldsymbol{x}$에 대해서 예측되는 label은 각 class에 대한 softmax의 값 중 가장 큰 값을 갖는 label이다.

$$\hat{y}(\boldsymbol{x})=\arg \max_{i} S_{i}(\boldsymbol{x} ; T)$$

각 class에 대한 softmax는 다음과 같다.

$$\tag{1} S_{i}(\boldsymbol{x} ; T)=\frac{\exp \left(f_{i}(\boldsymbol{x}) / T\right)}{\sum_{j=1}^{N} \exp \left(f_{j}(\boldsymbol{x}) / T\right)} $$

이 때, $T \in \mathbb{R}^{+}$가 바로 양의 실수 값을 갖는 temperature scaling parameter이다. 학습시에는 1로 고정된다. 즉, 일반적인 softmax를 동일하게 사용하므로 pre-trained network를 수정할 필요가 없다. 그리고 input $\boldsymbol{x}$에 대해 가장 큰 softmax의 값을 softmax score라고 하며 다음과 같이 표현할 수 있다.

$$S_{\hat{y}}(\boldsymbol{x} ; T)=\max_{i} S_{i}(\boldsymbol{x} ; T)$$

Temperature scaling을 사용함으로써 in- and out-of-distribution image의 softmax score의 gap을 크게 만들어준다. 구체적으로는 in-distribution의 softmax score를 더 크게 만들게 된다.

Input Preprocessing

Input에 다음과 같은 small perturbation을 넣어주면 in-distribution의 softmax score를 크게 만들어줄 수 있다고 한다.

$$\tag{2} \tilde{\boldsymbol{x}}=\boldsymbol{x}-\varepsilon \operatorname{sign}\left(-\nabla_{\boldsymbol{x}} \log S_{\hat{y}}(\boldsymbol{x} ; T)\right) $$

이 때 perturbation을 얼마나 강하게 줄지는 $\epsilon$을 통해 결정하게 된다. 저자에 따르면 이 아이디어는 Goodfellow의 adversarial examples에서 얻었다고 한다. 이렇게 perturbation을 주었을 때 out-distribution보다 in-distribution에서 영향이 강하게 나타나 둘을 분리하기가 더 쉬워진다고 말하고 있다.

Out-of-distribution Detector

위의 두 방법을 조합해 OOD detection을 한다. 주어진 input image $\boldsymbol{x}$에 대해서 (2)를 사용해 preprocessing을 거쳐 $\tilde{\boldsymbol{x}}$를 만든 뒤, pre-trained network에 넣고 calibrated softmax score인 $S(\tilde{\boldsymbol{x}}; T)$를 계산하고 이 score를 threshold $\delta$와 비교해 OOD 여부를 결정한다. In-distribution의 sample이 더 큰 score를 갖는다는 걸 전제로 한다. Detector는 다음의 식으로 표현할 수 있다.

$$ g(\boldsymbol{x} ; \delta, T, \varepsilon)=\begin{cases} 1 & \operatorname{if } \max_{i} p(\tilde{\boldsymbol{x}} ; T) \leq \delta \cr 0 & \operatorname{if } \max_{i} p(\tilde{\boldsymbol{x}} ; T) \geq \delta \end{cases} $$

이 때, $T, \epsilon, \delta$는 true positive rate이 95%가 되도록 맞춰준다.

Experiments

Section 3의 내용이 ODIN의 전부이다. 여기서부터는 실제로 ODIN을 적용했을 때 실제로 OOD detection에 효과적인지를 검증한다.

Introduction에서 언급한 성능이 바로 DenseNet을 CIFAR-10에 대해 학습시키고 TinyImageNet (crop)을 찾는 task에서의 성능으로 95% TPR기준으로 34%에서 4.2%로 FPR이 대폭 개선된 것을 보여준다. 그리고 ROC curve자체도 분류의 성능이 크게 개선되었음을 보여준다. 이외에도 다양한 성능향상에 대한 실험결과가 있지만 이 포스팅에서는 생략한다.

Discussion

이 section에서는 왜 temperature scaling과 input preprocessing의 효과가 있었는지에 대해 논의한다.

Analysis on Temperature Scaling

Temperature scaling의 식 (1)을 Taylor expansion을 사용해 정리해주면 아래와 같이 된다. Taylor Series의 세 번째 항 이상은 무시한다.

$$\tag{3} S_{\hat{y}}(\boldsymbol{x} ; T) \approx \frac{1}{N-\frac{1}{T} \sum_{i}\left[f_{\hat{y}}(\boldsymbol{x})-f_{i}(\boldsymbol{x})\right]+\frac{1}{2 T^{2}} \sum_{i}\left[f_{\hat{y}}(\boldsymbol{x})-f_{i}(\boldsymbol{x})\right]^{2}} $$

분석을 용이하게 하기위해 다음 두 항을 정의하자. 각각은 (3) 분모의 두 번째, 세 번째 항에 대응된다.

$$ U_{1}(\boldsymbol{x})=\frac{1}{N-1} \sum_{i \neq \hat{y}}\left[f_{\hat{y}}(\boldsymbol{x})-f_{i}(\boldsymbol{x})\right] $$

$$ U_{2}(\boldsymbol{x})=\frac{1}{N-1} \sum_{i \neq \hat{y}}\left[f_{\hat{y}}(\boldsymbol{x})-f_{i}(\boldsymbol{x})\right]^{2} $$

$U_{1}$은 network의 output이 다른 클래스의 output과 평균적으로 얼마나 차이가 나는지를 나타내는 지표이다. 값이 클 수록 다른 class와 분명하게 구분된다고 할 수 있다. $U_{2}$는 분산과 비슷하게 다른 score들 간에 얼마나 떨어져 있는지를 나타낸다.

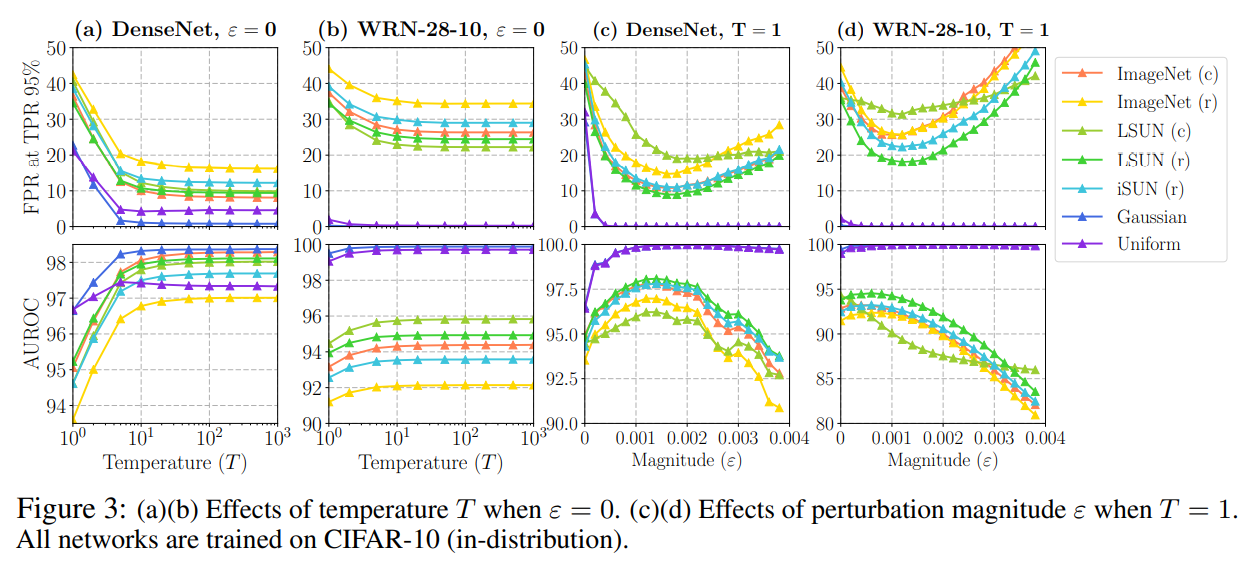
Figure 3의 (a), (b)를 보면 temperature를 올릴수록 FPR이 감소하고 AUROC가 증가하는 것을 볼 수 있다. 그리고 $T$가 일정수준 이상으로 커지게 되면 softmax score는 사실상 $U_{1}$에 의해 결정이 되고 $U_{2}$의 영향은 미미해지면서 saturation이 된다.

Analysis on Input Preprocessing

Input preprocessing이 유효한 이유는 gradient의 크기와 관련이 있다. 논문에서는 log-softmax의 first order Taylor expansion으로 이를 설명한다.

$$ \log S_{\hat{y}}(\tilde{\boldsymbol{x}} ; T)=\log S_{\hat{y}}(\boldsymbol{x} ; T)+\varepsilon\lVert\nabla_{\boldsymbol{x}} \log S_{\hat{y}}(\boldsymbol{x} ; T)\rVert_{1}+o(\varepsilon) $$

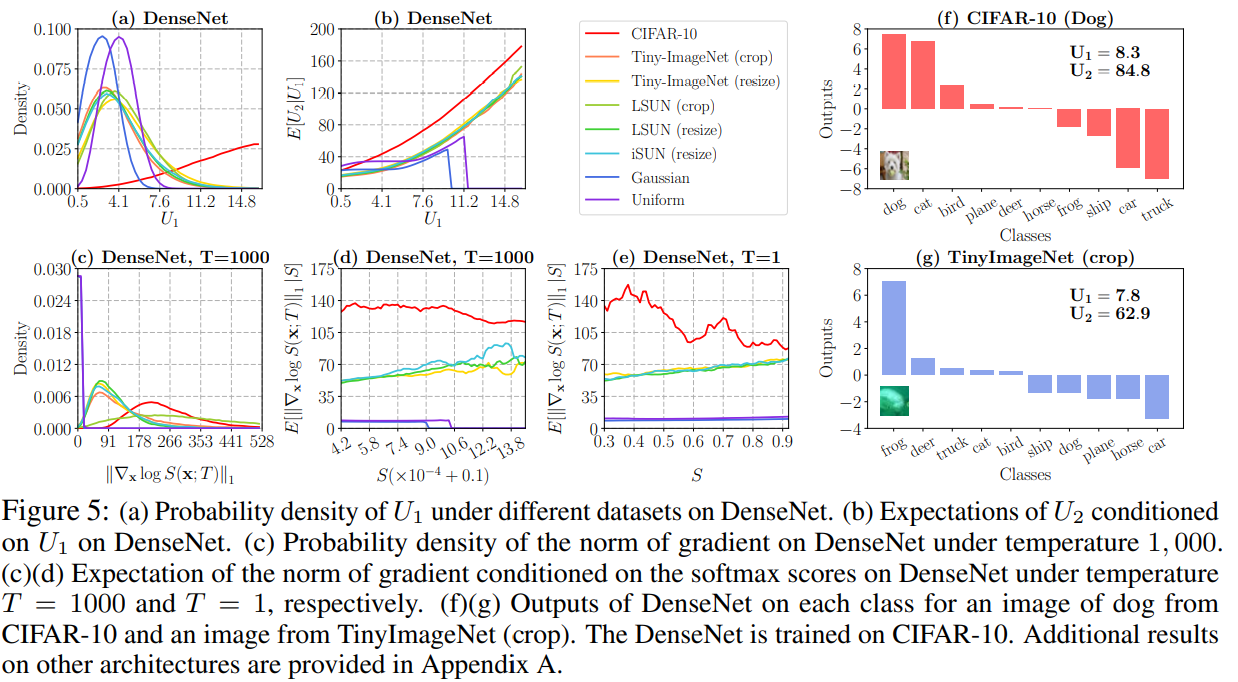
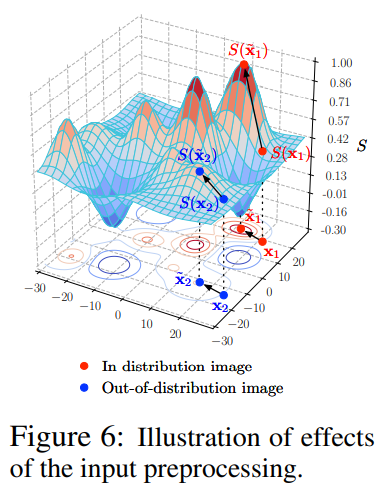
여기서 gradient term이 가지는 중요한 성질은 대부분의 경우 log-softmax의 gradient가 OOD보다 in-distribution에서 더 큰 값을 갖는다는 것이다. Figure 5의 (c)를 보면 대부분의 경우 in-distribution인 CIFAR-10에서 훨씬 큰 gradient를 갖고 있음을 볼 수 있다. Figure 5의 (d)를 보아도 같은 softmax score에서 in-distribution일 때의 gradient 기대값이 OOD일 때보다 훨씬 크게 나타나는 것이 확인된다. 이를 그림으로 표현하면 아래와 같다.

In-distribution image $\boldsymbol{x}_{1}$과 OOD image $\boldsymbol{x}_{2}$를 비교해보자. 두 image가 비슷한 softmax score를 갖는다 하더라도 $(S(\boldsymbol{x}_{1}) \approx S(\boldsymbol{x}_{2}))$ input processing을 통해 perturbation을 주게 되면 앞서 언급한대로 in-distribution에서 더 큰 gradient를 갖게되어 gradient의 L1-norm도 더 클 것이므로 in-distribution의 image는 OOD보다 훨씬 큰 softmax score를 갖게 될 것이다. 따라서 in- and out-of-distribution image의 분리가 더 쉬워지게 된다. 주의할 점은 충분히 커지면 saturation되는 temperature의 성질과는 다르게 $\epsilon$은 sweet spot을 갖는 성질이 있어 지나치게 큰 $\epsilon$을 주게되면 오히려 성능이 떨어지게 된다. 이는 앞서 내린 추정이 Taylor expansion의 첫째 항까지만 보고 내린 결론인데 $\epsilon$이 커지게 되면 2차항 이상에서의 Taylor expansion항들의 영향이 커지면서 perturbation이 지나치게 커지게 되는 것으로 논문에서는 이야기한다.

Related Works and Future Directions

ODIN에서 사용한 두 가지 방법도 이론적으로 강력한 support를 갖는다고 보기는 어렵기에 저자 역시 두 방법이 이용한 성질인 (1) in-distribution에서 cross label간의 variance가 더 크다는 점, (2) log-softmax score가 in-distribution에서 더 큰 gradient를 갖는다는 성질을 더 잘 이해하여야 OOD 문제를 효과적으로 다룰 수 있을 것이라고 언급한다.

Conclusions

이 논문은 ODIN이라는 OOD detector를 제시하였다. 기존에 있던 baseline보다 훨씬 좋은 성능을 보여주고 있음을 확인하는 실험을 수행하였고 ODIN에 사용된 방법이 왜 효과적인지에 대한 empirical analysis도 수행하였다.

Bibliography

Liang, Shiyu, Yixuan Li, and Rayadurgam Srikant. “Enhancing the reliability of out-of-distribution image detection in neural networks.” arXiv preprint arXiv:1706.02690 (2017).