LSGAN: Least Square Generative Adversarial Networks

LSGAN은 GAN의 discriminator에 약간의 변형으로 효과적인 성능향상을 기대할 수 있는 방법이다.

Abstract

GAN은 현재 generative model을 언급할 때 주요한 흐름 중 하나이다. 하지만 GAN을 “잘” 훈련시키기는 사실 쉽지 않다. 여러 이유가 있지만 이 논문에서는 주요한 이유중 하나인 vanishing gradient를 다룬다. 기존 GAN의 loss function에서 발생하는 vanishing gradient문제를 완화할 수 있는 Least Squares Generative Adversarial Networks(LSGAN)을 제시하며 LSGAN에서 제시하는 loss function을 줄이는 것은 수학적으로는 Pearson $\chi^2$를 줄이는 것과 같다는 것도 보인다. LSGAN은 간단한 변형임에도 불구하고 LSGAN을 적용한 generator가 만드는 결과물의 품질은 기존방식보다 유의하게 높으며 훈련도 안정적으로 할 수 있다는데 의의가 있다고 생각한다.

Introduction

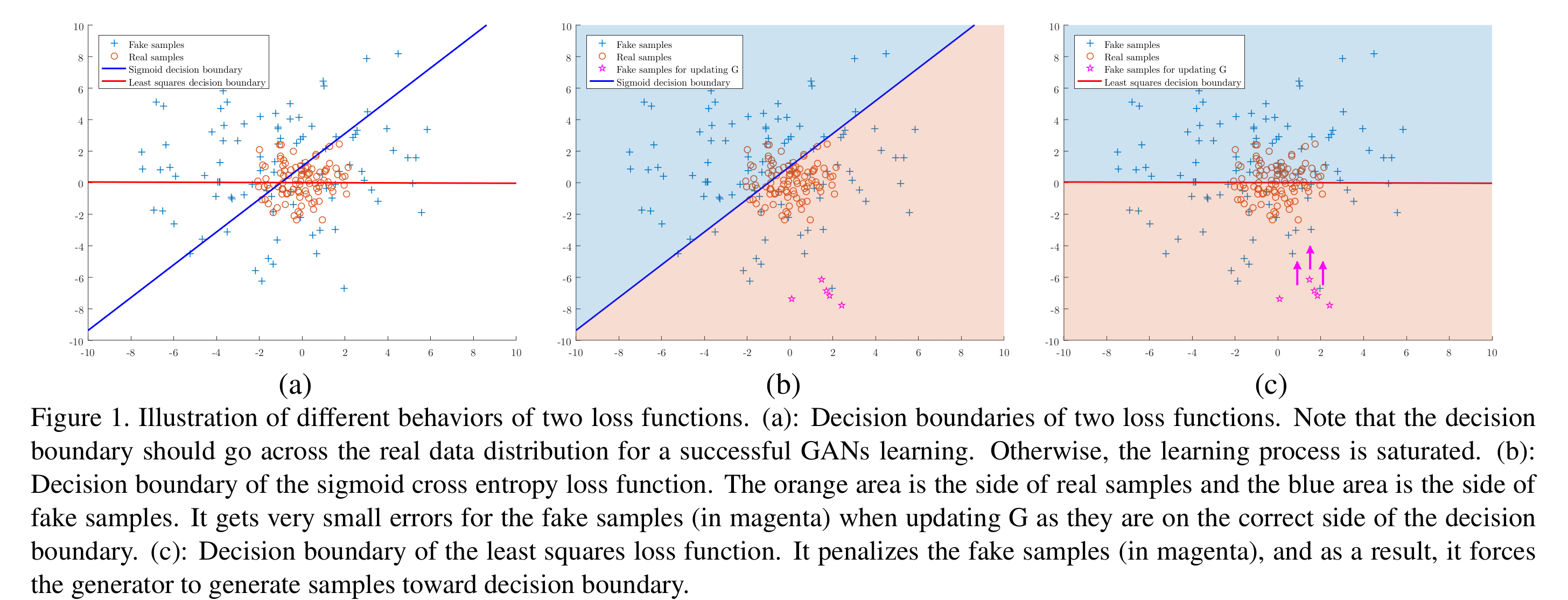
Deep learning을 활용한 generative model에 대한 논의는 RBM, DBM, VAE등과 같은 방법들에서부터 논의되어왔다. 하지만 이러한 방식들은 approximation method와 intractable function에 의존한다는 한계로 인해 효과적인 생성모델로 사용하기가 어려웠으며 이러한 제약을 없앤 GAN의 등장과 함께 GAN에 기반한 다양한 generative model이 파생되기 시작했다. 이 논문은 GAN의 discriminator에 주모한다. GAN의 discriminator는 generator가 만든 결과물이 진짜인지 가짜인지 판단하는 역할로 output layer에 보통 sigmoid가 붙어 진짜 혹은 가짜일 확률로 바꾸어주고 이에 대한 cross entropy loss를 줄이는 방식으로 학습해왔다. 이 논문에서 주목하는 부분은 generator의 학습 과정에서 생성된 fake 데이터를 real data로 discriminator가 분류하기는 했지만 real data와는 차이가 있는 sample에 대해서 gradient가 사라지는 문제이다. 정리하면 sigmoid는 진짜, 가짜 데이터로 분류된지에 대해서는 적절한 loss를 제공할 수 있지만 진짜로 판단한 sample이 실제 real data distribution에서 얼마나 떨어져 있는지에 대해서는 반영할 수 없다는 맹점이 있고 이를 극복하고자 하는 것이 LSGAN이다. 이와 관련한 자세한 논의는 Figure 1과 함께 언급한다.

LSGAN에서 제시하는 loss function은 위의 경우를 구분함으로써 discriminator에 의해 real data라고 판정된 fake data에 penalty를 주어 fake sample들이 decision boundary로 움직이도록 해준다. Real data라고 판단한 sample들을 실제 real data와 가깝게 만들어 줌으로써 보다 높은 품질의 generation이 가능해지는 것이다. 뿐만 아니라 decision boundary로부터의 거리에 대해 penalty가 적용되므로 더 많은 gradient가 발생해 vanishing gradient문제가 완화되어 학습도 보다 안정적으로 된다고 한다.

Related Work

Deep generative model의 흐름에 대해 성립한다. RBM, DBM, VAE를 언급하고 GAN에 대해 언급한다. 기존 방식에 비해 GAN은 별도의 approximation method없이 적용할 수 있다는 장점이 있으며 기존과는 다른 패러다임을 만들어 냈다. 하지만 GAN을 실제로 적용해보면 훈련이 쉽지 않다는 사실을 느끼게 된다. Deep convolutional generative adversarial network(DCGAN)이 등장하면서 GAN이 생성하는 이미지의 품질이 비약적으로 상승하게 되며 DCGAN은 이미지 생성에 있어 안정적으로 훈련할 수 있는 GAN구조를 제시하였다는데 큰 의의가 있다. 이후 파생된 많은 GAN들은 DCGAN에서 사용한 아이디어를 계승하게 된다. 이후 f-GAN논문에서 original GAN이 사용하고 있는 Jensen-Shannon divergence는 다양한 divergence estimation의 특수한 경우이며 임의의 함수로 divergence를 정의해 사용할 수 있음을 보이고 이를 f-divergences라고 한다.

Method

Generative Adversarial Networks

Ian Goodfellow가 발표한 original GAN의 기본적인 내용을 정리한다. GAN은 minimax game을 하는 generative model로 discriminator는 생성된 데이터가 실제 학습데이터에서 온 것인지 generator가 만들어낸 것인지를 구분하는 역할이며 generator는 데이터를 만들어 discriminator로 하여금 실제 학습데이터에서 온 것으로 속여야 한다. 이 둘이 각자의 목적을 달성하기 위해 minimax game을 하는 것이 original GAN의 아이디어이며 다음과 같이 표현된다.

$$\tag{1} \min_{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim P_{\text {data}(\boldsymbol{x})}}[\log D(x)]+\mathbb{E}_{z \sim p_{\boldsymbol{z}(\boldsymbol{z})}}[\log (1-D(G(z)))] $$

Least Squares Generative Adversarial Networks

LSGAN에서는 objective function을 다음과 같이 정의한다.

$$ \begin{aligned}\tag{2} \min_{D} V_{\mathrm{LSGAN}}(D) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}\left[(D(\boldsymbol{x})-b)^{2}\right]+\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z}))-a)^{2}\right] \cr \min_{G} V_{\mathrm{LSGAN}}(G) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z}))-c)^{2}\right] \end{aligned} $$

식을 보면 original GAN이 cross entropy를 계산하는 반면 LSGAN은 discriminator가 입력받은 data가 LSGAN에서 부여한 code($a, b, c$)와 얼마나 떨어져있는지에 대해 계산하는 것을 볼 수 있다. 앞서 언급한대로 LSGAN에서는 기존 GAN에서는 구분하지 못했던 discriminator가 실제 데이터라고 판단하였으나 real data와는 떨어져있는 fake sample에 대해 penalty를 주어 gradient가 발생하게끔 한다. 여기서 부여되는 $a-b$ coding을 눈여겨보자. 이 기호는 이후 section에서도 사용되며 구현에 있어서 중요하다. $a$는 fake data를, $b$는 real data를 각각 나타내며 $c$는 $G$ 입장에서 자신이 생성한 fake data에 대해 $D$가 판단하기를 바라는 값이 된다.

Benefits of LSGANs

LSGAN의 장점은 계속 언급된 바와 같이 discriminator가 real data라고 판단했지만 real data와는 거리가 먼 sample에 대해 penalty를 부여할 수 있다는 것과 이로인해 vanishing gradient 문제를 오나화할 수 있다는 것이다.

Generator의 학습시점에서 discriminator는 고정되어있고 discriminator가 고정되어있다는 것은 decision boundary가 고정되었다는 것과 같다. 따라서 언급한 penalty가 반영되면 generator로 하여금 decision boundary쪽으로 sample을 생성되도록 할 수 있다. Decision boundary는 real data가 모여있어 구분하기 어려운 곳을 향하므로 GAN학습에서 기대하는 결과를 얻을 수 있게 된다.

Figure 1 (b)를 보면 sigmoid decision boundary를 기준으로 아래는 discriminator가 real data로 판단한 영역이다. 이 때 논문에서 문제로 삼고있는 부분은 magenta로 표시된 데이터, 즉 real data로 판단한 fake sample이지만 real data와는 동떨어져 있는 데이터에 대해 vanishing gradient문제가 생긴다는 것이다. 파란선이 decision boundary이므로 sigmoid의 heatmap을 그려보면 (10,0)에서 매우 높게 나타날 것이고 이미 magenta가 있는 공간은 기울기가 상당히 작은 공간일 것임을 생각해볼 수 있다. 반면 Figure 1(c)는 LSGAN의 decision boundary를 보여주는데 거리에 비례해 제곱을하는 특성상 gradient를 살리기가 용이하며 이러한 성질로 인해 magenta로 표시된 sample들을 real data의 영역으로 가져오기가 수월해진다.

Figure 2에서 보이듯이 sigmoid cross entropy는 일정수준 이상 값이 커지면 기울기가 매우 작아지고 이런 영역에서 vanishing gradient가 발생할 것임을 짐작할 수 있다. 하지만 least squre loss function은 $x=0$인 지점 이외에서는 모두 기울기값이 존재하므로 이런 문제가 완화될 수 있다.

Relation to f-divergence

저자는 논문에서 LSGAN이 단순한 아이디어이지만 실제로 LSGAN을 사용하는 것은 $f$-divergence 관점에서 Pearson $\chi^2$ divergence에 대한 GAN과 같음을 보인다. Original GAN에서 밝혔듯, GAN의 구조는 기본적으로 Jansen-Shannon divergence를 최소화하는 것과 같다.

$$\tag{3} C(G)=K L\left(p_{\text {data }} \mid \frac{p_{\text {data }}+p_{g}}{2}\right)+K L\left(p_{g} \mid \frac{p_{\text {data }}+p_{g}}{2}\right)-\log (4) $$

$f$-divergence의 관점에서 LSGAN을 보기 위해 LSGAN의 objective는 다음과 같이 표현할 수 있다.

$$\tag{4} \begin{aligned} \min_{D} V_{\mathrm{LSGAN}}(D) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{x} \sim p_{\text{data}}(\boldsymbol{x})}\left[(D(\boldsymbol{x})-b)^{2}\right] \cr &+\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z}))-a)^{2}\right] \cr \min _{G} V_{\mathrm{LSGAN}}(G) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data}}(\boldsymbol{x})}\left[(D(\boldsymbol{x})-c)^{2}\right] \cr &+\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z}))-c)^{2}\right] \end{aligned} $$

Generator term에서 추가된 항은 discriminator에 대한 식만 포함하므로 $V_{\text{LSGAN}}(G)$을 최소화하는데는 변화가 없다. $a$가 fake data, $b$가 real data를 나타내는데 사용되었으므로 고정된 generator에 대한 optimal discriminator $D$는 다음과 같이 표현할 수 있다.

$$\tag{5} D^{*}(\boldsymbol{x})=\frac{b p_{\text {data }}(\boldsymbol{x})+a p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})} $$

이를 잘 정리하면 다음과 같다.

$$\tag{6} \begin{aligned} 2 C(G) &=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{d}}}\left[\left(D^{*}(\boldsymbol{x})-c\right)^{2}\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{z}}\left[\left(D^{*}(G(\boldsymbol{z}))-c\right)^{2}\right] \cr &=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{d}}}\left[\left(D^{*}(\boldsymbol{x})-c\right)^{2}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\left(D^{*}(\boldsymbol{x})-c\right)^{2}\right] \cr &=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{d}}}\left[\left(\frac{b p_{\mathrm{d}}(\boldsymbol{x})+a p_{g}(\boldsymbol{x})}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}-c\right)^{2}\right] \cr &+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\left(\frac{b p_{\mathrm{d}}(\boldsymbol{x})+a p_{g}(\boldsymbol{x})}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}-c\right)^{2}\right] \cr &=\int_{\mathcal{X}} p_{\mathrm{d}}(\boldsymbol{x})\left(\frac{(b-c) p_{\mathrm{d}}(\boldsymbol{x})+(a-c) p_{g}(\boldsymbol{x})}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right)^{2} \mathrm{~d} x \cr &+\int_{\mathcal{X}} p_{g}(\boldsymbol{x})\left(\frac{(b-c) p_{\mathrm{d}}(\boldsymbol{x})+(a-c) p_{g}(\boldsymbol{x})}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right)^{2} \mathrm{~d} x \cr &=\int_{\mathcal{X}} \frac{\left((b-c) p_{\mathrm{d}}(\boldsymbol{x})+(a-c) p_{g}(\boldsymbol{x})\right)^{2}}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})} \mathrm{d} x \cr &=\int_{\mathcal{X}} \frac{\left((b-c)\left(p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})\right)-(b-a) p_{g}(\boldsymbol{x})\right)^{2}}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})} \mathrm{d} x \end{aligned} $$

$b-c=1$, $b-a=2$라고 하면 이 식은 아래와 같이 정리된다.

$$\tag{7} \begin{aligned} 2 C(G) &=\int_{\mathcal{X}} \frac{\left(2 p_{g}(\boldsymbol{x})-\left(p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})\right)\right)^{2}}{p_{\mathrm{d}}(\boldsymbol{x})+p_{g}(\boldsymbol{x})} \mathrm{d} x \cr &=\chi_{\text {Pearson }}^{2}\left(p_{\mathrm{d}}+p_{g} | 2 p_{g}\right) \end{aligned} $$

즉, generator가 최소화하는 것은 결국 $p_{d} + p_{g}$와 $2p_{g}$의 Pearson $\chi^2$를 최소화 하는 것과 같음을 보인 것이다. 다만, 주의할 점은 앞서 언급된 $b-c=1$, $b-a=2$를 만족해야 Pearson $\chi^2$에 대한 최소화로 의미를 부여할 수 있다.

Parameter Selection

실제 구현에 있어서 매우 중요한 부분이다. LSGAN을 사용하기 위해서 남아있는 문제는 $a, b, c$를 결정하는 것이다. 이 때 만족해야 하는 것은 $b-c=1$, $b-a=2$이다. 논문에서는 크게 두 가지 세팅을 언급한다.

처음 제시하는 세팅은 $a=-1, b=1, c=0$이다. 이 경우 objective function은 다음과 같다.

$$\tag{8} \begin{aligned} \min _{D} V_{\mathrm{LSGAN}}(D) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}\left[(D(\boldsymbol{x})-1)^{2}\right] \cr &+\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z}))+1)^{2}\right] \cr \min _{G} V_{\mathrm{LSGAN}}(G) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z})))^{2}\right] \end{aligned} $$

다른 방식은 $a=0, b=c=1$을 부여하는 binary coding scheme이다. 사실 이 경우가 직관적으로 받아들이기는 더 수월하다. Discriminator는 real data(1)와 fake data(0)을 구분해야하며 generator는 자신이 만드는 sample이 discriminator에게 1로 보여지기를 바라는 상황에 대응시키면 된다. 이 때 objective function은 다음과 같다.

$$\tag{9} \begin{aligned} \min _{D} V_{\mathrm{LSGAN}}(D) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}\left[(D(\boldsymbol{x})-1)^{2}\right] \cr &+\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z})))^{2}\right] \cr \min _{G} V_{\mathrm{LSGAN}}(G) &=\frac{1}{2} \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}\left[(D(G(\boldsymbol{z}))-1)^{2}\right] . \end{aligned} $$

(9)의 setting이 (8)보다 original GAN에서 바꿔 도입하기가 용이하므로 (9)가 사용하기가 더 편리하며 논문에서도 두 setting에서 동일한 성능을 확인했고 저자도 (9)의 setting을 사용하였다고 한다.

Model Architectures

이미지 생성을 하기위해 사용한 architecture를 소개한다. DCGAN의 아이디어를 차용하였으며 중국어 문자를 만드는 문제는 한자가 워낙 많다보니 lilnear mapping을 사용해 먼저 label vector를 작은 vector로 만들고 모델에 concatenate했다는 실용적인 팁이 언급된다.

Experiment

결과적으로 비교하는 EBGAN, DCGAN보다 높은 품질의 이미지 생성에 성공하였다.

사진으 ㅣ품질을 비교하는 방법은 여러가지가 있겠지만 가장 눈에 띄는 것은 해상도 자체가 이전 GAN에 비해 육안으로 쉽게 파악할 수 있을만큼 향상된 것을 볼 수 있다. 특히 DCGAN에서 보이는 이미지의 자글자글함이 많이 개선된 형태로 나타난다.

Mode collapse에 대해서도 batch normalization과 optimizer를 바꾸어가며 훈련시켰을 때 original GAN보다 더 robust한 양상을 보임을 확인했다고 한다.

Conclusion

이 논문에서는 GAN의 vanishing gradient문제를 완화할 수 있고 보다 안정적인 학습이 가능한 LSGAN을 제시하였다. LSGAN은 generated sample을 decision boundary로 가져오는 역할을 해주지만 더 이상적인 상황은 generated sample을 real data territory로 움직이는 것으로 이러한 방향을 future work으로 언급하며 논문은 마무리된다.

Bibliography

Mao, Xudong, et al. “Least squares generative adversarial networks.” Proceedings of the IEEE international conference on computer vision. 2017.