2.7: Linear Mappings

벡터공간을 다루면서 벡터공간의 벡터들은 스칼라로 곱해지거나 벡터끼리 더해질 수 있으며 닫혀있는 성질로 인해 그 결과 역시 벡터로써 벡터공간에 속한다. 이번 포스팅에서는 선형변환(linear mapping) 에 대해서 다룬다. 당연하게도 변환은 정의하기 나름이며 다양한 형태의 변환을 만들 수 있다. 하지만 선형변환은 특별한 성질이 있다. 바로 이름에서 유추해볼 수 있듯, 선형성(linearity)이 성립한다.
선형변환이 특별한 이유는 아래와 같은 선형성, 즉 벡터공간의 구조를 보존해 이론을 발전시켜 나아갈 수 있기 때문이다.
$$ \begin{aligned} \Phi(\boldsymbol{x}+\boldsymbol{y}) &=\Phi(\boldsymbol{x})+\Phi(\boldsymbol{y}) \cr \Phi(\lambda \boldsymbol{x}) &=\lambda \Phi(\boldsymbol{x}) \end{aligned} $$
Linear Mapping
선형변환은 다음과 같이 정의한다.
행렬은 그 자체로 선형변환을 나타내며 이에 대한 내용은 이후 행렬분해에서 자세히 다루도록 한다.
Injective, Surjective, Bijective
어떤 변환 $\Phi$는 domain, codomain, range에 따라 다음과 같이 분류할 수 있다.
Injective
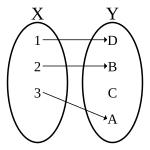
Wikipedia: Bijection, injection and surjection
임의의 집합 $\mathcal{V}$, $\mathcal{W}$에 대해서, 변환 $\Phi: \mathcal{V} \rightarrow \mathcal{W}$이 다음을 만족하면 injective라고 한다.
$$\forall \boldsymbol{x}, \boldsymbol{y} \in \mathcal{V} : \Phi(\boldsymbol{x}) = \Phi(\boldsymbol{y}) \Rightarrow \boldsymbol{x} = \boldsymbol{y}$$
Surjective
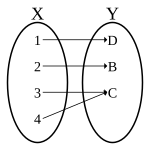
Wikipedia: Bijection, injection and surjection
임의의 집합 $\mathcal{V}$, $\mathcal{W}$에 대해서, 변환 $\Phi: \mathcal{V} \rightarrow \mathcal{W}$이 다음을 만족하면 surjective라고 한다.
$$\Phi(\mathcal{V}) = \mathcal{W}$$
Bijective

Wikipedia: Bijection, injection and surjection
임의의 집합 $\mathcal{V}$, $\mathcal{W}$에 대해서, 변환 $\Phi: \mathcal{V} \rightarrow \mathcal{W}$이 injective, surjective를 모두 만족하면 bijective라고 한다.
Special Linear Mappings
다음은 선형변환의 특수한 예로 위의 관계를 통해 표현할 수 있다.
- Isomorphism: $\Phi: V \rightarrow W$ linear and bijective
- Endomorphism: $\Phi: V \rightarrow V$ linear
- Automorphism: $\Phi: V \rightarrow V$ linear and bijective
Properties of Linear Mapping
선형변환은 다음의 성질을 갖는다.
- $\Phi: V \rightarrow W$, $\Psi: W \rightarrow X$가 선형변환이면, $\Psi \circ \Phi: V \rightarrow X$도 선형변환이다.
- $\Phi: V \rightarrow W$가 isomorphism이면 $\Phi^{-1}: W \rightarrow V$도 isomorphism이다.
- $\Phi: V \rightarrow W$, $\Psi: V \rightarrow W$가 선형변환이면, $\Phi + \Psi$와 $\lambda \in \mathbb{R}$인 $\lambda \Phi$도 선형변환이다.
Matrix Representation of Linear Mapping
Coordinates
좌표를 생각할 때 보통 가장 먼저 떠오르는 것은 Cartesian 좌표계일 것이다. 하지만 극좌표계도 있으며 기준이 되는 벡터를 무엇으로 하는지에 따라 다양하게 정의할 수 있다. 즉 basis를 무엇으로 삼느냐에 따라 좌표계는 다르게 정의될 수 있다. 좌표는 다음과 같이 정의된다.
Transformation Matrix
$n$개의 ordered basis $B = (\boldsymbol{b}_1, \ldots, \boldsymbol{b}_n)$를 가지는 벡터공간 $V$와 $m$개의 basis $C = (\boldsymbol{c}_1, \ldots, \boldsymbol{c}_m)$를 가지는 벡터공간 $W$을 생각해보자. 이 때 선형사상 $\Phi: V \to W$는 다음과 같이 나타낼 수 있다.
즉, $V$의 각 basis에 대한 변환이 $W$의 basis $C$로 유일하게 표현된다면 우리는 각 basis의 선형결합 계수들로 transformation matrix를 만들 수 있다.$V$는 $\boldsymbol{b}_j$의 span이므로 $V$의 모든 basis에 대한 변환이 $W$공간에서 유일하게 표현된다면, $V$공간의 좌표에 대해 basis를 변환시키는 선형결합을 그대로 적용해주면 공간에 대한 변환이 되는 것도 직관적으로 이해해볼 수 있다. 이를 각각의 벡터에 대해 적용하면 변환은 다음처럼 쓸 수 있다.
만약 $\hat{\boldsymbol{x}}$이 $\boldsymbol{x} \in V$의 좌표벡터이고 $\hat{\boldsymbol{y}}$가 $\boldsymbol{y} = \Phi(\boldsymbol{x}) \in W$의 좌표벡터라면 다음이 성립한다.$$\hat{\boldsymbol{y}} = \boldsymbol{A}_{\Phi}\hat{\boldsymbol{x}}$$
서술이 길었지만 간단하게 보면 어떤 벡터에 대한 행렬의 곱은 벡터공간에서 벡터공간으로의 변환이며, 벡터공간의 좌표를 변환하는 벡터공간의 좌표로 바꾸어주는 연산인 것이다.
Basis Change
여기서 다루는 basis 변환(basis change)개념은 이후 eigendecomposition, SVD와 같은 행렬 분해방법의 기초가 되는 내용이다. 우선 basis change에 대한 정의를 살펴보자.
하나의 변환을 여러 변환으로 단계적으로 분해한 것으로 정성적으로도, 정량적으로도 이해하기가 쉽다. 하지만 얼핏 보면 $\tilde{B}$에서 $\tilde{C}$로의 변환이 존재한다면 해당 변환행렬을 바로 쓰면 될 것을 굳이 이렇게 분해해야하는 의문이 들 수도 있다. 변환의 결과만 본다면 맞는 말이다. 하지만 이후에 다룰 eigendecomposition이나 SVD를 사용하면 중간의 매개가 되는 벡터공간을 이용하여 중요한 component를 추출해 공간변환을 압축할 수 있고, $V$, $W$내에서의 유사도가 높은 벡터들을 확인할 수 있다. 또한 차원을 바꿔버림으로써 kernel trick을 사용해 현재 공간에서는 풀기 어려운 문제를 고차원으로 올려 쉽게 풀 수도 있다. 이처럼 다양한 응용을 할 수 있게되는데 이러한 내용의 기초가 되는 것이 바로 basis change이다.
이러한 꼴은 앞으로도 자주 다루어지므로 익숙해지도록 하자. 위의 성질을 통해 행렬의 equivalence와 similarity를 정의할 수 있다. 특히, similarity는 자주 언급되는 성질이므로 눈여겨보자.
Equivalence
Similarity
Similar 관계에 있는 행렬은 항상 equivalent하지만 equivalent관계에 있는 행렬이 꼭 similar하지는 않다는 점을 명심하자.
Image(Range) and Kernel(Null Space)
Kernel과 image는 벡터공간에 대해 선형변환이 가지는 중요한 성질들이다.
Kernel(Null Space)
Kernel은 다음과 같이 정의된다.
Kernel은 여러 분야에서 의미가 상당히 많이 overloading되어있는 단어지만 선형대수학에서의 의미는 간단하다. 변환에 의해 $\boldsymbol{0}$, 즉 영벡터로 mapping되는 벡터의 집합이다.
Image (Range)
Image는 다음과 같이 정의 된다.
Image는 함수의 치역(range)과 그 의미가 완전히 같다. $\Phi$라는 변환(함수)에 대한 $V$의 치역이다. 같은 관점에서 $V$는 정의역(domain), $W$는 공역(codomain)에 대응된다.
Properties
벡터공간 $V$, $W$에 대해서 선형변환 $\Phi: V \rightarrow W$은 다음의 성질을 갖는다.
-
$\Phi(\boldsymbol{0}_{V}) = \boldsymbol{0}_{W}$가 항상 성립하며 따라서 $\boldsymbol{0}_{V} \in \operatorname{ker}(\Phi)$이다. 특히 null space는 어떠한 경우에도 최소한 $\boldsymbol{0}$을 원소로 갖는다.
벡터공간 $V$에서의 $\boldsymbol{0}$는 선형변환을해서 $W$공간으로 이동시켜도 $\boldsymbol{0}$이다. 따라서 kernel의 정의에 따라 $\boldsymbol{0}$은 항상 null space의 원소가 된다.
-
$\operatorname{Im}(\Phi) \subseteq W$는 $W$의 부분공간이며 $\operatorname{ker}(\Phi) \subseteq V$는 $V$의 부분공간이다.
$\operatorname{Im}(\Phi) \subseteq W$의 등호는 surjective할 때 성립한다. 위의 성질에의해 kernel도 설명이 된다.
-
$\Phi$가 injective인 것은 $\operatorname{ker}(\Phi) = \lbrace \boldsymbol{0}\rbrace$과 동치이다.
변환 $\Phi$의 kernel이 $\boldsymbol{0}$만 원소로 갖는다는 것은 변환한 공간 $W$에서 $\boldsymbol{0}$로 대응되는 것이 $V$공간에서 $\boldsymbol{0}$밖에 없다는 뜻이다. 쉽게 생각해보면 $\boldsymbol{Ax} = \boldsymbol{0}$의 해가 $\boldsymbol{x} = \boldsymbol{0}$밖에 없다는 것은 역행렬이 존재한다는 뜻이며 injective에 해당한다.
-
$\boldsymbol{A} = [\boldsymbol{a}_{1}, \ldots, \boldsymbol{a}_{n}]$으로 $\boldsymbol{a}_{i}$가 $\boldsymbol{A}$의 열일 때 다음을 얻을 수 있다. $$ \begin{aligned} \operatorname{Im}(\Phi) &=\left\lbrace\boldsymbol{A} \boldsymbol{x}: \boldsymbol{x} \in \mathbb{R}^{n}\right\rbrace=\left\lbrace\sum_{i=1}^{n} x_{i} \boldsymbol{a}_{i}: x_{1}, \ldots, x_{n} \in \mathbb{R}\right\rbrace \cr &=\operatorname{span}\left[\boldsymbol{a}_{1}, \ldots, \boldsymbol{a}_{n}\right] \subseteq \mathbb{R}^{m} \end{aligned} $$
이 때, image는 $\boldsymbol{A}$의 열벡터의 span으로 column space라고 부른다. 따라서 column space는 $\mathbb{R}^{m}$의 부분공간이다.
-
$\operatorname{rk}(\boldsymbol{A}) = \operatorname{dim}(\operatorname{Im}(\Phi))$
-
Kernel은 homogeneous 선형시스템 $\boldsymbol{Ax} = \boldsymbol{0}$의 일반해로 $\boldsymbol{0} \in \mathbb{R}^{m}$을 만드는 $\mathbb{R}^{n}$의 모든 선형결합을 표현한다.
-
Kernel은 $\mathbb{R}^{n}$의 부분공간이다.
-
Kernel은 열벡터의 관계를 다루며 다른 열을 표현하기위한 선형결합을 어떻게 구성할지 찾는데 사용할 수 있다.
Rank-Nullity Theorem
Properties
- 만약 $\operatorname{dim}(\operatorname{Im}(\Phi)) < \operatorname{dim}(V)$이면 $\operatorname{ker}(\Phi)$는 $\boldsymbol{0}_{V}$이외의 non-trivial kernel을 갖는다.
- 행렬 $\boldsymbol{A}_{\Phi}$가 $\Phi$의 oredered basis에 대한 변환행렬이고 $\operatorname{dim}(\operatorname{Im}(\Phi)) < \operatorname{dim}(V)$이면 선형방정식 $\boldsymbol{A}_{\Phi} \boldsymbol{x} = \boldsymbol{0}$은 무한히 많은 해를 갖는다.
- $\operatorname{dim}(V) = \operatorname{dim}(W)$라면 $\operatorname{Im}(\Phi) \subseteq W$가 성립하며 다음은 모두 참이다.
- $\Phi$는 injective이다.
- $\Phi$는 surjective이다.
- $\Phi$는 bijective이다.