InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets

기존 GAN의 구조에서 mutual information을 최대로 만들도록 학습하는 GAN을 제시한 논문이다.

Abstract

이 논문은 기본적인 GAN(Generative Adversarial Networks)의 구조에 약간의 변형을 통해 GAN으로 하여금 데이터의 mutual information을 크게 만드는 representation을 찾도록 학습시키는 방식을 제시한다. 정확한 mutual information을 objective로 사용하지는 못하지만 mutual information에 대한 lower bound를 수학적으로 보이고 이 lower bound를 maximize하는 문제로 formulation 하였다. InfoGAN은 GAN에 interpretable representation을 부여하였다는데 큰 의의가 있다고 생각한다.

Introduction

Introduction에서는 비지도학습 관점에서 representation learning을 언급한다. 특히 데이터가 가지는 특징을 뚜렷하게 구분할 수 있는 형태로 분리해낼 수 있다면 데이터의 특징을 파악하기도 훨씬 수월할 것이다. 논문에서 나오는 핵심단어 중 하나는 disentangled representation이다. 어떤 정보가 주어졌을 때 그 정보간에 뚜렷하게 구분할 수 있는 특징으로 분리하는 의미로 받아들이고 있다. 예로 MNIST 숫자에 어떤 변환이 있다고 한다면 그 변환을 글씨 두께, 회전과 같이 구분되는 정보로 나누어 볼 수 있다면 generative model 관점에서는 각각을 조절할 수 있는 것이니 분명한 이점이 생기게 된다. 저자는 이러한 관점에서 GAN으로 하여금 disentangled representation을 학습하도록 하는데 목적이 있음을 밝히고 있다.

We present a simple modification to the generative adversarial network objective that encourages it to learn interpretable and meaningful representations.

실제로 GAN구조에서 변경되는 점은 매우 간단하다. GAN의 noise variable의 일부에 mutual information을 최대화하도록 하는 것이다.

Related Work

Related work에서는 정보를 압축하는 아이디어로써의 autoencoder나 Boltzmann machine을 언급하고 InfoGAN의 기반이 되는 GAN, 그리고 disentangled representation을 찾기 위한 선행 연구들을 소개한다. 특히, disentangled representation과 관련해 언급된 연구는 지도학습 기반이었으며 InfoGAN은 비지도학습을 사용함으로써 labelled data가 필요하지 않다는 점을 강조한다.

Background: Generative Adversarial Networks

Ian Goodfellow가 발표한 GAN의 기본적인 내용을 정리한다. GAN은 minimax game을 하는 generative model로 목적은 generator가 가지는 분포 $P_{G}(x)$로 하여금 실제 데이터 분포인 $P_{\textrm{data}}(x)$를 학습하는 것이다. 이전의 generative model과 달리 분포를 복잡하게 정의할 필요 없이 noise variable $z \sim P_{\textrm{noise}}(z)$에서 출발해 $G(z)$를 학습시킨다. Adversarial network인 이유는 discriminator와 generator가 적대적인 관게에 있기 때문이다. 원 논문의 비유를 따르자면 discriminator는 위조지폐를 감별해내야 하는 역할이며 generator는 discriminator를 속여야 하는 역할을 맡는다. GAN의 이러한 minimax game은 다음과 같이 표현할 수 있다.

$$\tag{1} \min_{G} \max _{D} V(D, G)=\mathbb{E}_{x \sim P_{\text {data }}}[\log D(x)]+\mathbb{E}_{z \sim \text { noise }}[\log (1-D(G(z)))] $$

Mutual Information for Inducing Latent Codes

기본적인 GAN의 구조에서 사용하는 input noise vector $z$는 특별한 제약없이 사용한다. 따라서 generator가 사용하는 input인 noise vector의 정보는 entangled 되어있다고 할 수 있다. noise vector에서 데이터의 semantic feature를 직접 대응시키기가 어렵다. 하지만 데이터는 여러 semantic factor로 구성되어 있다. 앞서 언급한 MNIST의 숫자도 회전이나 글자의 두께 같이 의미를 갖는 요소로 분리해서 생각해볼 수 있다.

이 논문은 semantic feature를 input noise에서 분리하는 방법을 다루므로 input vector를 다음과 같이 구분해 표기한다.

1. $z$: source noise로 GAN에서 사용하는 일반적인 noise이다.
2. $c$: latent code로 이 논문의 목적은 이 latent code로 data distribution의 뚜렷한 semantic feature를 찾는 것이다.

Latent code는 $c_1, c_2, \ldots, c_{L}$로 여러개의 code로 구성할 수 있다. Latent code는 $P(c_{1}, c_{2}, \ldots, c_{L}) = \prod_{i=1}^{L}P(c_{i})$로 factored distribution을 가정한다.

이제 GAN이 unsupervised 방식으로 이 latent code를 구분하도록 만들어야 하는데 생각해볼 문제는 GAN이 latent code를 무시하면서 학습할 수도 있다는 것이다. 즉 latent code에 대한 가중치를 낮게 잡으면서 사실상 사용하지 않는 학습을 할 가능성이 있으므로 이를 억제하기 위한 장치가 필요하다. 이를 위해 정보이론에서의 mutual information 개념을 도입하게 된다.

$X$와 $Y$의 mutual information $I(X; Y)$은 $Y$를 알게됨으로 인해 얻게되는 $X$에 대한 정보량이다. 정보량은 entropy를 사용해 다음과 같이 표현할 수 있다.

$$\tag{2} I(X; Y) = H(X) - H(X \mid Y) = H(Y) - H(Y \mid X)$$

$X$라는 정보량에서 $Y$를 알고 있을 때의 정보량을 뺀 값이므로 $X$의 정보과 $Y$의 정보와 전혀 상관이 없었다면 $I(X; Y) = 0$이 될 것이고 $Y$에 의해 $X$의 정보가 영향을 많이 받는다면 (관련이 크다면) $I$는 커지게 된다. 이러한 개념을 사용해 information-regularized minimax game을 다음과 같이 정의한다.

$$\tag{3} \min_{G} \max_{D} V_{I}(D, G)=V(D, G)-\lambda I(c ; G(z, c)) $$

오른쪽 항의 두 번째 term을 살펴보자. $G(z, c)$가 $c$와 무관한 정보를 만들어 냈다면 $I \rightarrow 0$이 된다. $G$관점에서는 $V_{I}(D, G)$를 작게 만들어야하는데 $I \rightarrow 0$이면 불리하다. 따라서 $c$가 $G(z, c)$에 의해 많은 영향을 받도록해야 generator는 $v_{I}$를 잘 줄일 수 있게 된다. 따라서 위의 minimax game을 풀면 앞서 제기된 $c$가 무시되는 상황을 억제할 수 있게 된다.

Variational Mutual Information Maximization

Mutual information을 크게 만들어 위의 minimax game을 푸는 것으로 문제 formulation을 하였지만 실제로는 mutual information을 푸는 것은 간단한 일이 아니다. $I(c;G(z,c))$는 posterior $P(c \mid x)$를 알아야 하는데 애초에 generative model이 posterior를 알았다면 이렇게 어렵게 갈 필요도 없었을 것이다. Posterior를 사용하지 않고 mutual information을 최대화하기 위해 저자는 posterior $P(c \mid x)$를 근사하는 auxiliary distribution $Q(c \mid x)$의 lower bound를 찾는 문제로 바꾸고 lower bound를 구한다. 개인적으로는 이 부분이 논문의 가장 큰 contribution이라고 생각한다.

Lower bound는 다음과 같이 유도된다.

$$\tag{4} \begin{aligned} I(c ; G(z, c)) &=H(c)-H(c \mid G(z, c)) \cr &=\mathbb{E}_{x \sim G(z, c)}\left[\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log P\left(c^{\prime} \mid x\right)\right]\right]+H(c) \cr &=\mathbb{E}_{x \sim G(z, c)}[\underbrace{D_{\mathrm{KL}}(P(\cdot \mid x) | Q(\cdot \mid x))}_{\geq 0}+\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid x\right)\right]]+H(c) \cr & \geq \mathbb{E}_{x \sim G(z, c)}\left[\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid x\right)\right]\right]+H(c) \end{aligned} $$

Lower bound를 위와 같이 잡음으로써 posterior $P(c \mid x)$를 사용하는 것은 피했지만 아직도 posterior에서 sampling을 하는 부분이 포함되어 있다. 아래의 Lemma를 사용해 sampling하는 부분도 바꾸어 줄 수 있다.

$I(c; G(z,c))$의 lower bound는 아래와 같이 $L_{I}(G, Q)$로 나타낼 수 있다.

$$\tag{5} \begin{aligned} L_{I}(G, Q) &=E_{c \sim P(c), x \sim G(z, c)}[\log Q(c \mid x)]+H(c) \cr &=E_{x \sim G(z, c)}\left[\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid x\right)\right]\right]+H(c) \cr & \leq I(c ; G(z, c)) \end{aligned} $$

Lemma를 오른쪽에서 왼쪽으로 가는 방향으로 식(5)의 둘째줄에서 첫째줄로 적용해준 것이다. 이렇게하면 posterior에서의 sampling을 사용하지 않고 표현하게 된다. 또한 식을 보면 $L_(G, Q)$는 $\log Q(c \mid x)$에 대한 기대값이므로 기대값 안쪽을 여러번 뽑아 평균내면 추정할 수 있다.(Monte Carlo simulation) Sampling부분은 neural network에서 reparameterization trick으로 처리해주면 된다. 이렇게 함으로써 GAN의 훈련과정을 바꾸지 않고도 Information Maximizing Generative Adversarial Networks (InfoGAN) 구조를 만들 수 있다.

정리하면 InfoGAN은 기존 GAN을 다음의 minimax game으로 바꾼다. variational regularization of mutual information이 추가된 형태이며 $\lambda$는 hyperparameter이다.

$$\tag{6} \min_{G, Q} \max _{D} V_{\operatorname{InfoGAN}}(D, G, Q)=V(D, G)-\lambda L_{I}(G, Q) $$

Implementation

구현측면에서는 GAN에서 많은 구조가 바뀌는게 아니라 비교적 간단하게 구현할 수 있다. Posterior를 근사하는 $Q$도 network이므로 $Q$와 $D$는 noise에서 generator를 통과하는 구조를 모두 공유하며 마지막에 $Q(c \mid x)$를 위한 network $Q$가 추가된다. 따라서 기본적인 GAN에서 추가되는 parameter는 많지 않다. 그리고 추가적으로 얻는 장점은 InfoGAN은 일반적인 GAN에 비해 수렴속도가 더 빠르다고 한다.

Categorical latent code $c_{i}$에 대해서는 softmax로 $Q(c_{i} \mid x)$를 표현하며 continuous latent code $c_{j}$에 대해서는 ture posterior의 분포를 뭐로 보느냐에 따라 다양한 선택지가 있지만 논문에서는 factored Gaussian을 $Q(c_{j} \mid x)$로 사용했다고 한다.

InfoGAN에서 추가된 hyperparameter $\lambda$는 하나뿐이라서 tuning하기 수월하며 discrete latent codes에는 1로 고정해 사용해도 충분했다고 한다. Continuous latent code의 경우는 1보다 작은 값이 주로 사용되었다고 한다.

GAN자체가 훈련이 어려운 만큼 DC-GAN에서 사용한 기법들을 그대로 사용하였다고 한다.

Experiment

실험해서 확인하는 가장 중요한 것은 정말로 InfoGAN을 사용할 때 mutual information이 maximized되는지를 확인하는 것이다. 두 번째로는 학습한 InfoGAN모델에서 disengtangled and interpretable representation이 찾아졌는지를 보는 것으로 generator에서 latent factor를 바꿔가면서 실험해보면 이를 확인할 수 있다.

Mutual Information Maximization

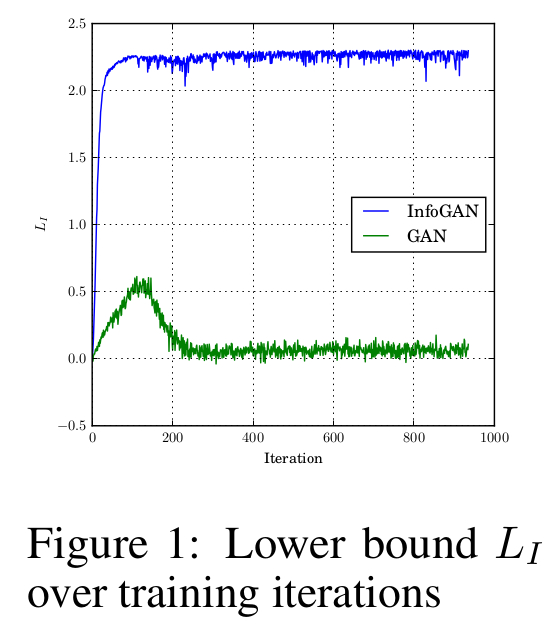
학습에 mutual information $L_{I}(G,Q)$가 직접 사용되므로 학습시키면서 이 값이 증가하는지를 확인하면 mutual information을 증가시키는 학습이 되는지를 판단할 수 있다. 해당 term이 없는 기본 GAN과 비교해보면 더욱 확실히 비교할 수 있을 것이다.

MNIST에 대해서 학습을 시켰으며 $c \sim \textrm{Cat}(K=10, p=0.1)$로 $c$는 categorical distribution에서 sampling한다.

아래의 Figure 1을 보면 GAN은 mutual information이 증감을 거치고 일정값을 유지하는 반면 InfoGAN은 증가 후 유지됨은 물론 그 값자체가 InfoGAN보다 훨씬 큰 값을 갖는다.

Disentangled Representation

Disentangled representation을 확인하는 실험도 MNIST에서 이루어지며 세 개의 latent code를 사용해 실험한다. $c_{1}$은 categorical code로 $c_{1} \sim \textrm{Cat}(K=10, p=0.1)$, 두 개의 latent code는 연속값을 갖는 code로 $c_{2}, c_{3} \sim \textrm{Unif(-1, 1)}$에서 sampling한다.

Figure 2는 InfoGAN의 핵심을 보여준다. 우선 (a)를 보면 $c_{1}$은 discrete latent code로 $\textrm{Cat}(K=10, p=0.1)$에서 sampling하는 것을 생각할 때 정확하게 의도한 결과를 얻었음을 보여준다. 둘째행의 마지막 숫자는 오류가 있지만 10개의 class에 대해 supervision없이 수행한 값으로 정확하게 10개의 숫자가 있음을 구분해낸 것이다. 다른 두 개의 continuous latent code가 보여주는 결과도 매우 흥미롭다. 비록 $\textrm{Unif}(-1, 1)$에서 sampling했지만 더 대비되는 결과를 보기 위해 저자는 값을 -2 ~ 2로 바꾸어가면서 generator의 출력을 그려 각각 (c), (d)에서 보여주었다. (c)에서는 기울기가, (d)에서는 굵기가 latent code화 되었음을 볼 수 있다. 이는 의도한 disentangled and interpretable의 성질을 충분히 뒷받침하는 결과이다. Faces와 chairs에 대해서도 이와 유사한 결과를 보여준다.

Conclusion

이 논문에서는 representation learning algorithm으로 InfoGAN을 제시하였다. 이전 접근법들과 대비되는 점은 supervision이 필요없이 unsupervised learning으로써 representation learning을 할 수 있음을 보였다는 점이며 interpretable and disentangled representation을 효과적으로 잡았다는데 있다. 계산비용에 있어서도 기존 GAN에 약간의 계산이 더해지는 정도라 매우 효율적이다.

Bibliography

Chen, Xi, et al. “Infogan: Interpretable representation learning by information maximizing generative adversarial nets.” Proceedings of the 30th International Conference on Neural Information Processing Systems. 2016.