HER: Hindsight Experience Replay

HER

2021-05-22 5936 words 12 minutes

Contents

Hindsight experience replay(HER)는 agent에게 binary reward가 sparse하게 주어지는 상황에서 sample-efficient한 학습을 할 수 있도록 해주는 방법이다.

Abstract

강화학습이 어려운 이유 중 하나로 꼭 언급되는 것 중 하나가 sparse reward이다. 보상이 즉각적으로 발생하는 경우도 있지만 많은 경우 강화학습에서의 보상은 sparse하다. 게임이 한참 진행되고 승리, 혹은 패배로 +1, -1을 받거나 로봇에게 태스크를 수행하도록했을 때 목표의 달성여부가 결정될 때 비로소 보상이 발생한다. 저자는 binary reward가 sparse한 상황에서 data sample을 효율적으로 사용해 학습하는 방식인 HER를 제시한다. 이 방법은 off-policy RL 알고리즘과 함께 사용될 수 있고 implicit한 curriculum learning으로 볼 수 있다고 말한다. 논문 제목을 하나씩 살펴보면 hindsight, ‘일이 발생한 후’라는 뜻을 갖고 있으므로 행동결과 이후에 일어나는 일에 무언가 해보겠다라는 추론을 해볼 수 있고 experience replay는 DQN에서 사용되었듯 경험을 축적해 놓고 학습하는 방식으로 off-policy에서만 사용가능할 것임을 예상해 볼 수 있다.

Introduction

강화학습, 특히 robotics에서는 task에 적확한 reward function을 설정하는 것이 매우 중요하다. 이러한 cost engineering은 그 자체로 RL에 대한 이해와 적용하는 task의 domain-pecific 지식까지 알아야한다는 어려움이 있어 강화학습을 실세계에 적용하는데 큰 어려움이 된다. 심지어 domain 지식이 있다고 하더라도 observation으로 판단할 수 있는 상황 자체가 복잡하다면 reward의 설계는 더욱 어려워진다. 이런 상황을 감안할 때 task의 성공여부로 정의되는 간단한 binary reward signal이 다듬어지지 않은(unshaped) 상황에서 학습할 수 있는 방법론의 실용성은 상당하다고 볼 수 있다.

저자는 직관적으로 논문의 방향을 잘 표현하는 예시를 언급한다. 논문 출판 당시 model-free RL 알고리즘들은 보상이 발생하는, 즉 원하는 결과로 부터 학습을 할 지언정, 보상이 발생하지 않는 결과로 부터는 학습을 하지 못한다. 반면, 사람은 이와 다르게 반면교사나 타산지석이라는 말에서 보이듯 원치않은 결과로부터 학습을 할 수 있다. 당신이 하키운동을 하고있고 puck(아이스 하키의 공)을 골 네트에 넣는 상황이라고 해보자. Puck을 쳤는데 골 네트에 들어가지 못하고 오른쪽으로 가버린 상황이라면 RL agent는 성공적이지 못한 shot이었고 이 경험으로부터 거의 학습할 수 없을 것이다. 하지만 관점을 다르게 해보자. 만약, 골 네트가 더 오른쪽에 있었다고 한다면 이 경험은 성공적인 경험으로 볼 수 있게 된다. 이 관점에 HER가 제시하는 관점이다. 논문에서는 이러한 방식을 사용했을 때 sample efficiency가 향상되고 sparse, binary reward에 대해 학습을 향상시킨다고 언급한다. HER의 핵심아이디어는 episode를 replay할 때 agent가 달성하고자 하는 goal말고도 episode내에서 달상한 goal에 대해서 학습해 task 전반에 대한 이해도를 올리는데 있다.

The pivotal idea behind HER is to replay each episode with a different goal than the one the agent was trying to achieve, e.g. one of the goals which was achieved in the episode.

Background

Reinfocement Learning

강화학습과 관련된 논문이므로 강화학습에서 사용되는 기본적인 notation을 정리한다. 논문에서 언급하든 standard reinforcement learning formalism을 사용하여 특별한 내용은 없다. Q-function에 대해 언급하며 Bellman optimality equation에서의 Q-function은 다음과 같이 표현된다.

$$ Q^{*}(s, a)=\mathbb{E}_{s^{\prime} \sim p(\cdot \mid s, a)}\left[r(s, a)+\gamma \max_{a^{\prime} \in \mathcal{A}} Q^{*}\left(s^{\prime}, a^{\prime}\right)\right] $$

Deep Q-Networks (DQN)

Nature에도 실린 유명한 DQN논문에 대해서 소개한다. DQN은 discrete action space에서 적용할 수 있는 model-free RL 알고리즘으로 off-policy의 장점을 살려 이전 경험들을 모아서 학습하는 replay buffer를 두고 있으며 안정적인 학습을 위해 main network의 가중치를 일정주기로 update하고 고정해서 사용하는 target network를 도입한였다.

Deep Deterministic Policy Gradients (DDPG)

DDPG는 DQN이 discrete action space에서만 작동하는 한계점을 인식하고 continuous action space에서도 사용 가능하도록 한 model-free RL 알고리즘이다. DDPG도 마찬가지로 target network개념을 사용하며 actor critic network를 기반으로 학습대상이 아닌 network는 freeze해서 사용하는 방식을 사용한다.

Universal Value Function Approximators (UVFA)

UVFA는 DQN을 하나 이상의 목표에 대해 사용할 수 있도록 확장한 논문이다. $\mathcal{G}$가 가능한 goal의 집합이라고 할 때 원소 $g \in \mathcal{G}$는 각각 대응하는 reward function $r_{g}: \mathcal{S} \times \mathcal{A} \rightarrow \mathcal{R}$이 있다. 핵심 아이디어는 각각의 episode는 state-goal pair 분포 $p(s_{0}, g)$에서 초기상태와 goal을 샘플링하고 시작한다는 것이다. 이 때 sampling된 goal은 episode가 진행하는동안 고정된다. Goal이 여러개 존재하는 상황이므로 각각의 timestep에서 agent는 현재 state뿐만 아니라 goal도 입력을 받게 된다. 즉 $\pi: \mathcal{S} \times \mathcal{G} \rightarrow \mathcal{A}$이고 reward는 $r_{t} = r_{g}(s_{t}, a_{t})$이다. Q-function도 state-action pair와 더불어 goal에도 의존적으로 되어 $Q^{\pi}(s_{t}, a_{t}, g) = \mathbb{E}[R_{t} \mid s_{t}, a_{t}, g]$이다. 논문에서는 이 Q-function에 대한 approximator를 학습시킴으로써 greedy policy가 학습때 보지 못했던 state-action pair에 대해서도 일반화할 수 있음을 보였다.

Hindsight Experience Replay

A Motivating Example

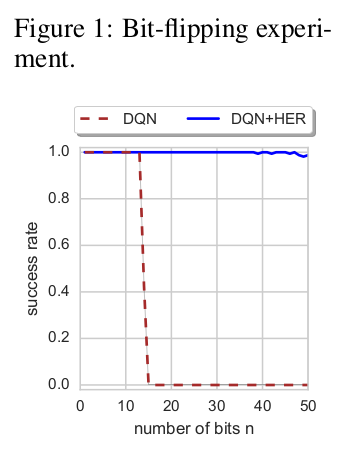
HER를 이해하기 위해서 다음의 bit-flipping 환경을 생각해보자. $n$개의 bit로 구성된 array가 있다고 생각하고 각각의 상태는 0, 1로 $\mathcal{S} = \lbrace 0, 1 \rbrace^{n}$이다. Action space $\mathcal{A} = \lbrace 0, 1, \ldots, n-1 \rbrace$로 action은 해당 $i$번째의 bit를 0에서 1로, 또는 1에서 0으로 바꾸는게 된다. 모든 epsisode는 시작할 때, 초기상태와 최종상태를 sample하고 policy는 target state에 있지 않을 때 -1의 보상을 받는다. 이 reward function을 수식으로 표현하면 $r_{g}(s, a) = -\lbrack s \neq g \rbrack$이다.

이러한 환경에서 일반적인 RL 알고리즘은 $n>40$인 상황에서 실패하게 된다. $n$에 대한 상태공간의 크기가 $2^{n}$임을 생각해보면 $n>40$은 매우 큰 환경이고 agent입장에서는 사실상 -1만 보상으로 받는 경우가 대부분이 된다. Exploration을 장려하는 방식들도 있지만 현재 상황에서의 문제는 exploration을 잘못했다기보다는 탐색공간의 절대적인 크기 자체가 크다는게 문제이므로 exploration에 대한 기법은 도움이 되지 않는다.

적절한 shaped reward function을 사용하면 이러한 문제를 벗어날 수 있다. 예를 들어 $r_{g}(s,a) = -\lVert s - g \rVert^{2}$과 같은 reward function이 있다고 해보자. 이 reward는 각 bit의 값 차이가 많이날수록 reward를 깎아먹게 되는데 달성하고자 하는 목표를 지도학습의 MSE를 사용하는 것과 같으므로 학습이 효율적으로 일어나 위의 문제를 해결할 수 있게 해준다. 실제로 논문에서 toy example에 대해서 이와 같은 방법을 통해 문제를 해결했다고 한다. 하지만 이러한 방식은 복잡한 문제상황에서는 이러한 직관적으로 간단하게 생각해볼 수 있는 shaped reward를 만들기가 어려우므로 사용하기가 어렵다.

Shaped reward를 사용하는 대신 어떠한 domain 지식 없이도 사용할 수 있는 다른 방식을 이 논문에서 제시한다. 다음과 같은 episdoe가 있다고 해보자.

$$ s_1, \ldots, s_{T} $$

$$ g \neq s_{1}, \ldots, s_{T} $$

Episode는 $s_{1}$에서 $s_{T}$까지 진행되었으며 goal $g$는 $T$ step까지 발생하지 않은 상황이다. 따라서 모든 상태에 대해 보상은 -1밖에 없다. 핵심 아이디어는 각각의 episode에 대해서 다른 goal로 바라보는 것이다. 이 예제에서 trajectory는 $g$를 target으로 할 때 학습할 수 있는 정보가 없다. 하지만 이 trajectory는 $s_{T}$까지 가는 방법에 대한 정보를 갖고 있다. Off-policy RL 알고리즘의 experience replay를 이용하면 이 경험을 통해 정보를 얻을 수 있다. 가령 experience replay에서 현재 설정된 $g$는 도달하지 못했지만 $s_{T}$에 도달했으므로 experience replay시에 $g$를 $s_{T}$로 바꾸게 된다면 이 경험을 통해 $s_{T}$까지의 trajectory를 통해 유의미한 학습을 할 수 있게 된다. 논문에서 언급한 방식은 $g$도 그대로 살려두고 같은 trajectory에서 $g$만 $s_{T}$로 바꾼 경로를 만들어 하나의 trajectory를 두 개로 구성하는 것이다. 이렇게하면 replay buffer는 두 배로 확장되며 이 중 절반은 $s_{T}$에 도달했으므로 -1이 아닌 보상값을 갖게되어 학습을 효율적으로 하게 된다.

Figure 1을 보면 이러한 접근방법이 효과적임을 볼 수 있다. Vanilla DQN의 경우는 $n \leq 13$에 대해서만 문제를 푼 반면 DQN에 HER를 적용한 경우는 $n=50$까지도 풀어낸다. 상태공간의 크기를 생각해보면 상당히 유의미한 결과라고 생각된다.

Multi-goal RL

저자는 하나 이상의 goal을 달성하는 agent의 학습에 관심이 있고 앞서 언급된 Universal Value Function Approximators방법에 따라 적용해보았다고 한다. 모든 goal $g \in \mathcal{G}$는 $f_{g}: \mathcal{S} \rightarrow \lbrace 0, 1 \rbrace$에 대응되며 goal에 agent가 도달했다면 $f_{g}(s) = 1$을 만족하게된다. Mapping $m$은 주어진 상태 $s$가 goal $g$에 도달하였는지에 대한 것으로 $m: \mathcal{S} \rightarrow \mathcal{G} \text{ such that } \forall_{ s \in \mathcal{S} } f_{m(s)} (s) = 1$과 같이 표현된다. 각각의 goal이 달성하고 싶은 상태일 때 $\mathcal{G} = \mathcal{S}$이고 $f_{g}(s) = \lbrack s = g \rbrack$으로 mapping $m$은 항등함수가 된다. 3.1의 문맥에서 state이 2차원 $(x,y)$이고 goal은 1차원이라고 한다면 mapping은 $m((x,y)) = x$가 된다.

Universal policy는 초기상태와 목표를 sampling한 임의의 RL 알고리즘에 대해 사용될 수 있다. 이 때 reward는 목표에 도달하지 못했을 때 음수값을 매 step에서 받게 된다. 하지만 이러한 방식은 reward function이 sparse해서 실제로는 잘 작동하지 않는다고 하며 이 문제를 극복하기 위해 저자는 HER를 도입하였다고 한다.

Algorithm

HER의 기본 아이디어는 간단하다. Episode를 진행하면 trajectory $s_{0}, \ldots, s_{T}$를 얻게 되며 각각의 transition은 replay buffer에 저장된다. 이 때 주어진 goal 뿐만이 아니라 실제로 경험한 마지막 상태를 goal로 하는 trajectory도 저장된다. Agent가 도착하고자 하는 goal은 agent의 action에는 영향을 주지만 environment dynamics에는 영향을 주지 않는다. 따라서 우리는 off-policy RL 알고리즘에서 각각의 trajectory를 임의로 가정한 목표로 replay 해볼 수 있다.

가장 간단한 HER은 각각의 trajectory goal을 $m(s_{T})$로 하는 것이다. 쉽게 말해, episode의 마지막에 도착한 상태를 goal로 사용한 것이다. 논문에서는 다양한 종류의 goal로 실험을 해보았으며 이는 4에서 자세히 다루어진다.

다음은 HER Algorithm이다.

순서대로 파악해보자. 우선 off-policy algorithm과 replay buffer를 초기화해준다. 이어서 정해진 수 만큼 episode를 실행한다. Episode가 시작되면 goal $g$를 sample하는 부분이 기존 방식과 큰 차이이며 초기 상태 $s_{0}$도 sampling해준다. Episode를 $T$-step만큼 off-policy algorithm $\mathbb{A}$의 policy에 따라 action을 선택하며 진행한다. 여기서 $T$-step을 진행하게 되면 한 episode에 대해서 trajectory를 얻게 된다. 이제 HER를 적용하는 단계이다. 방금 실행한 trajectory를 처음부터 sweep한다. 이 때 $t$에서의 보상 $r_{t} \coloneqq r(s_{t}, a_{t}, g)$가 된다. 그리고 주어진 goal $g$에 condition된 transition 값들을 replay buffer에 저장한다. 이 부분은 일반적인 experience replay buffer 저장 방법이다. 여기서 부터 HER를 적용하는데 replay에 사용할 추가 goal을 sample하게된다. $G \coloneqq \mathbb{S}$는 goal의 집합을 정의하는 것으로 앞서 정의한 strategy함수에 현재 episode를 넣어 얻은 것이다. 가장 간단한 strategy 함수는 마지막 상태 $s_{T}$를 goal로 사용하는 것이다. 이렇게 만든 $g^{\prime} \in G$에 대해서 새로운 reward $r^{\prime}$을 정의하고 마찬가지로 이 $g^{\prime}$에 condition된 transition을 저장한다. 여기서 $N$은 training epoch에 해당하며 주어진 $N$만큼 replay buffer에서 minibatch를 sample해 알고리즘 $\mathbb{A}$로 학습을 진행한다.

논문에 따르면 HER는 implicit curriculum learning으로 볼 수 있다고 한다. 바로 최종 goal을 사용하지 못하고 학습과정에서의 trajectory를 사용해 중간 단계의 state까지의 Q-value를 추정해 나아가는 것으로 볼 수 있을 것이다. Explicit curriculum learning은 상대적으로 쉬운 목표를 먼저 학습시키므로 환경을 기준으로 쉬운 목표를 설정해주어야 하는 반면 HER에서는 이미 사용한 경로를 통해 중간 과정들을 학습하므로 환경에 대해 control할 필요가 없다는 장점이 있다. HER는 sparse reward에 대해서도 작동하는 것이 확인되었고 shaped reward function보다도 잘 작동하였다고 한다.

Experiments

실험에는 7-DOF robot arm을 사용하였고 end-effector로는 two-finger gripper를 사용하였다. 시뮬레이션 환경은 MuJoCo physics engine을 사용하였다. 실험은 위의 영상에서 보여지듯 pushing, sliding, pick-and-place task에 대해 이루어졌다.

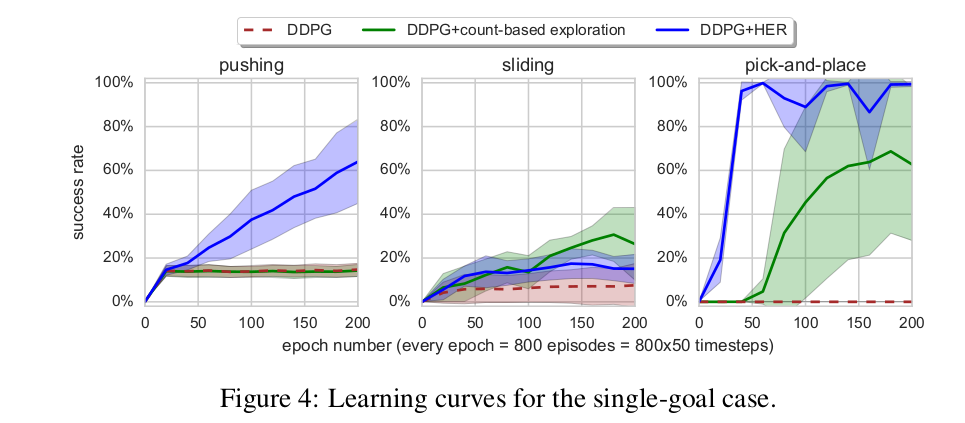
DDPG기준으로의 성능비교는 다음과 같다.

흥미로운 점은 multi goal이 아니라 single goal 환경에 대해서도 HER가 더 좋은 성능을 보여주었다는 점이다. 따라서 single goal인 학습환경에서도 HER를 사용하는 것이 권장된다고 한다.

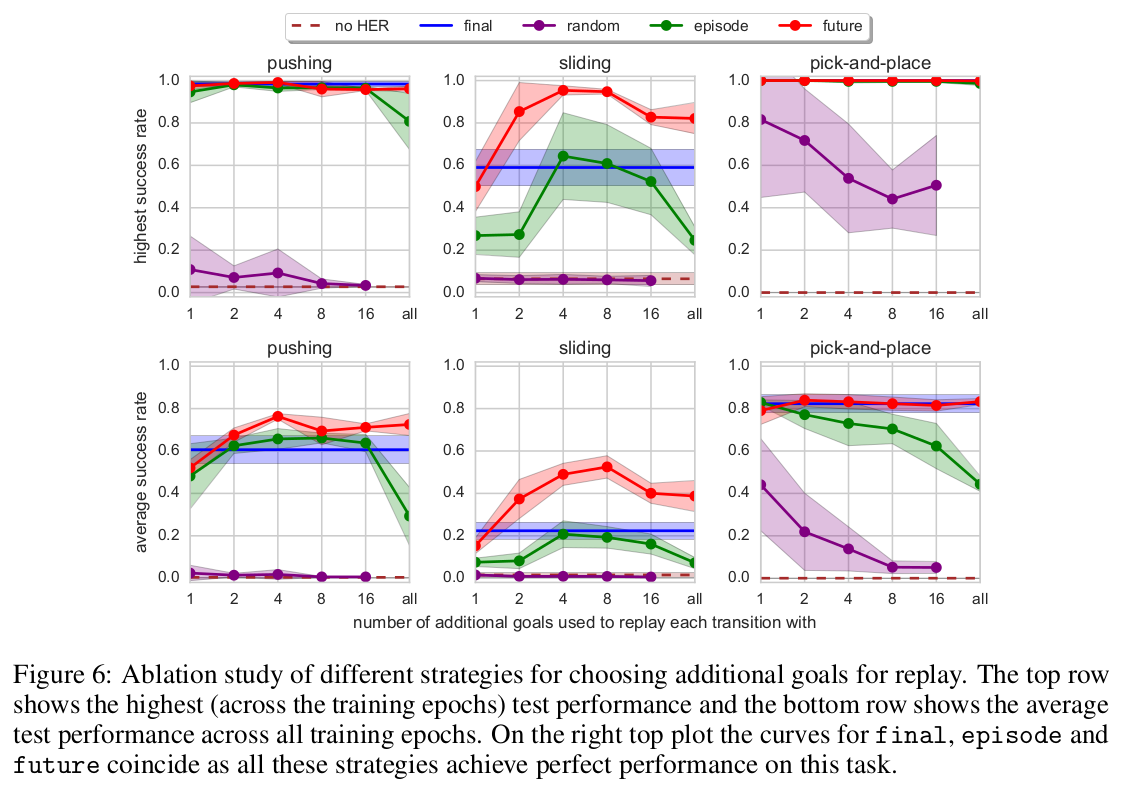
Goal sampling strategy $\mathbb{S}$로는 지금까지 마지막 state를 사용하는 것만 언급되었다. 실험에서는 다양한 goal sampling방법에 대해서도 실험을 하였다. Final은 지금까지 언급되었던 방식으로 경로에서 마지막 상태를 사용하는 방식이며 future는 replay를 할 때 동일 episode내에서 이전, 이후에 있는 state중에서 $k$개를 random하게 뽑는 방식이다. Episode는 동일 episode내에서 이전에 만난 상태들 중에서 $k$개의 random state를 뽑는 것이며 random은 훈련과정 전체를 통틀어 경험한 모든 상태 중에서 $k$개의 random state를 뽑는 것이다.

모든 setting에서 $k$는 hyperparameter이다. 실험환경에서는 future방식으로 $k$가 4~8일 때 가장 성능이 좋았다고 한다.

Related work에서는 experience replay와 관련된 기법과 multiple task에 대한 논문들이 소개된다. HER의 접근방법과 유사성이 있는 curriculum learning도 소개된다.

Conclusion

이 논문에서는 sparse and binary reward인 setting에서 off-policy RL알고리즘에 적용가능한 HER라는 방법론을 소개하였다. HER를 적용할 경우 vanilla RL 알고리즘이 실패한 task를 성공적으로 학습할 수 있음을 보였으며 실제 로봇을 사용한 실험에서도 잘 작동하는 것을 보여주었다.

Bibliography

Andrychowicz, Marcin, et al. “Hindsight experience replay.” arXiv preprint arXiv:1707.01495 (2017).