4.4 Eigendecomposition and Diagonalization

행렬의 eigenvalue와 eigenvector를 아는 것은 행렬이 만드는 변환에 대한 다양한 정보를 제공한다. 따라서 어떠한 행렬을 eigenvalue와 eigenvector를 볼 수 있는 형태로 분해할 수 있다면 유용하게 사용할 수 있을 것이다. 여기서는 정사각행렬에 적용할 수 있는 eigendecomposition에 대해 알아본다.
Eigenvalue와 eigenvector가 가지는 의미를 이전 문서에서 다루었다. Eigenvalue와 eigenvector를 어떻게 얻을 수 있을까? 물론, 이전 포스팅에서 언급된 정의식을 사용할 수 있다. 이번 문서에서는 나아가 eigendecomposition이라는 방법을 통해 eigenvector 및 eigenvector를 찾는 방법을 다룰 뿐만 아니라 벡터공간에서의 선형변환을 순차적인 행렬의 곱으로써 표현하는 방식에 대하여 다룬다.
Diagonal matrix
Diagonal matrix는 대각선 성분이외의 모든 성분이 0인 행렬을 의미하며 다음의 형태를 가진다.
$$ \boldsymbol{D} = \begin{bmatrix}c_{1} & \cdots & 0 \cr \vdots & \ddots & \vdots \cr 0 & \cdots & c_{n} \end{bmatrix} $$
Diagonal matrix는 determinant를 구할 때 편리할 뿐만 아니라, 거듭제곱이나 역행렬의 계산을 하는 것도 매우 편하게 바꾸어 준다. 당연한 성질처럼 느껴질 수도 있는데 이 당연한 성질로 인해서 어떤 행렬 또는 변환이 diagonal matrix를 포함한다면 유용한 성질을 쉽고 효율적으로 구할 수 있게된다. 그렇다면 임의의 행렬에서 diagonal matrix를 구하는 방법에 대해 알아보자.
Similar matrix $\boldsymbol{A}, \boldsymbol{D}$가 있다고 해보자. Invertible matrix $\boldsymbol{P}$가 존재한다면 similiarity 정의에 의해 다음과 같이 쓸 수 있다.
$$ \boldsymbol{D} = \boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P} $$
이 때, $\boldsymbol{D}$의 diagonal elements는 $\boldsymbol{A}$의 eigenvalue로 표현되고 $\boldsymbol{P}$는 해당하는 eigenvector이다. 다시말해 대각화하는 과정은 주어진 선형변환의 표현형을 eigenvector로 구성된 행렬과 eigenvalue를 대각성분으로하는 행렬로 분해하는 것이라 할 수 있다.
대각화가 가능한지는 다음을 통해 정의할 수 있다.
$\boldsymbol{A}$의 대각화를 한다는 것은 동일한 선형변환을 다른 basis를 사용해 표현하는 과정임을 알 수 있다. 이 때 바꾸는 basis가 $\boldsymbol{A}$의 eigenvector인 것이다.
Eigendecomposition
행렬 $\boldsymbol{A} \in \mathbb{R}^{n \times n}$와 스칼라 값 $\lambda_{1}, \ldots, \lambda_{n}$, $n$차원 벡터 $\mathbb{R}^{n}$ $\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}$에 대해서 벡터를 행렬 $\boldsymbol{P} \coloneqq [\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}]$로 표현하고 $\lambda_{1}, \ldots, \lambda_{n}$를 diagonal element로 가지는 $\boldsymbol{D} \in \mathbb{R}^{n \times n}$라고하자. 이 때, $\lambda_{1}, \ldots, \lambda_{n}$가 $\boldsymbol{A}$의 eigenvalue이고 $\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}$가 해당하는 eigenvector라면 다음과 같이 표현가능함을 보일 수 있다.
$$ \boldsymbol{AP} = \boldsymbol{PD} $$
이는 eigenvalue/vector정의만 이용하면 쉽게 증명이 가능하다.
$$ \begin{aligned} \boldsymbol{AP} &= \boldsymbol{A} [\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}] \cr &= [\boldsymbol{Ap}_{1}, \ldots, \boldsymbol{Ap}_{n}] \end{aligned} $$$$ \begin{aligned} \boldsymbol{PD} &= [\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}] \begin{bmatrix}\lambda_{1} & \cdots & 0 \cr \vdots & \ddots & \vdots \cr 0 & \cdots & \lambda_{n} \end{bmatrix} \cr &= [\lambda_{1} \boldsymbol{p}_{1}, \ldots, \lambda_{n}\boldsymbol{p}_{n}] \end{aligned} $$
위 두 결과를 각 성분에 대해 비교하면 eigenvalue/eigenvector 정의식이 된다.
$$ \begin{aligned} \boldsymbol{Ap}_{1} &= \lambda_{1}\boldsymbol{p}_{1} \cr &\vdots \cr \boldsymbol{Ap}_{n} &= \lambda_{n}\boldsymbol{p}_{n} \end{aligned} $$
따라서 $\boldsymbol{P}$의 열벡터들은 $\boldsymbol{A}$의 eigenvector에 해당함을 알 수 있다.
Diagnoalization은 $\boldsymbol{P}$가 full-rank로 invertible할 때 가능하다. 즉, 위의 eigenvector는 선형독립이다.
이제 eigendecomposition을 알아보자.
행렬 $\boldsymbol{A}$를 Symmetric matrix로 한정한다면 다음과 같은 더 강한 정리가 성립한다.
이는 Spectral theorem에서 바로 이어지는 내용이다. 상기해보자면 spectral theorem은 다음과 같다.
따라서 symmetric 행렬이라면 eigenvector가 orthonormal basis로 구성할 수 있음이 보장되고 이 경우에는 $\boldsymbol{D} = \boldsymbol{P}^{\top}\boldsymbol{A}\boldsymbol{P}$이 성립한다.
Geometric Intuition for the Eigendecomposition
Eigendecomposition이 행렬을 어떻게 분해하는지에 대해 알아보았다.
$$\boldsymbol{A} = \boldsymbol{PD} \boldsymbol{P}^{-1}$$
그렇다면 행렬 $\boldsymbol{A}$에 의한 변환 $\boldsymbol{Ax}$는 $\boldsymbol{PD} \boldsymbol{P}^{-1} \boldsymbol{x}$이다. 오른쪽부터 순서대로 행렬의 곱을 세차례에 걸쳐서 하게되며 각각의 곱도 선형변환으로써 의미를 갖는다. 여기서는 기하적으로 각각의 행렬곱에 의한 선형변환이 어떻게 벡터를 변환하는지 알아보자.
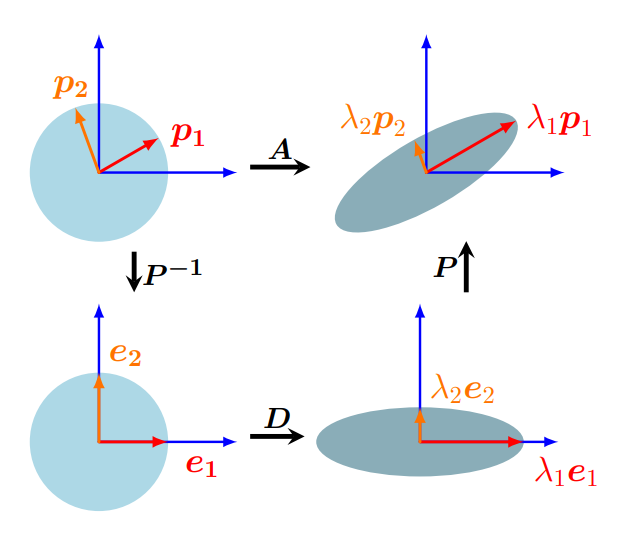
Eigendecomposition은 $\boldsymbol{A}$를 $\boldsymbol{PD} \boldsymbol{P}^{-1}$로 분해한다. 즉, 어떠한 벡터 $\boldsymbol{x}$의 $\boldsymbol{A}$에 대한 선형변환 $\boldsymbol{Ax}$는 $\boldsymbol{PD} \boldsymbol{P}^{-1} \boldsymbol{x}$와 같다. 따라서 벡터 $\boldsymbol{x}$는 왼쪽위에서 반시계반향으로 오른쪽 위까지 순차적인 변환된다.
제일 처음에 이뤄지는 연산은 $\boldsymbol{P}^{-1} \boldsymbol{x}$이다. $\boldsymbol{P}^{-1}$는 standard basis vector $\boldsymbol{e}_{i}$로 표현되는 공간으로 바꾸어주게 된다. 즉, eigenbasis $\boldsymbol{p}_{i}$를 standard basis vector로 변환해준다. (Fig 4.7 왼쪽하단) 그리고 diagonal matrix $\boldsymbol{D}$와 곱해지면서 각 basis가 eigenvalue $\lambda_{i}$만큼의 scaling이 이루어진다. (Fig 4.7 오른쪽 하단) 마지막으로, $\boldsymbol{P}$를 곱해주어 scaling된 basis vector를 다시 기존 공간으로 변환하게 된다. (Fig 4.7 오른쪽 상단)
정성적으로 이해하면, $\boldsymbol{A}$라는 변환을 바로 진행할 수도 있지만 각 basis에 대해 scaling만 하면 되는 공간으로 변환을 하고 scaling을 해준 뒤 다시 기존 공간으로 복원하는 과정으로 분해해 표현하는 것이 eigendecomposition이다. 예제를 통해 확인해보자.
Example
다음 행렬의 Eigendecomposition을 해보자.
$$ \boldsymbol{A} = \begin{bmatrix}2 & 1 \cr 1 & 2 \end{bmatrix} $$
Step 1: Compute eigenvalues and eigenvectors
Characteristic polynomial은 다음과 같이 구해진다.
$$ \begin{aligned} \text{det}(\boldsymbol{A} - \lambda \boldsymbol{I}) &= \text{det} \left( \begin{bmatrix} 2 - \lambda & 1 \cr 1 & 2 - \lambda \end{bmatrix} \right) \cr &= (2-\lambda)^2 - 1 \cr &= \lambda^2 - 4 \lambda +3 \cr &= (\lambda - 3)(\lambda -1) \end{aligned} $$
따라서 eigenvalue는 각각 $\lambda_{1} = 1, \lambda_{2} = 3$이다. 그리고 해당하는 eigenvector는 다음과 같다.
$$ \boldsymbol{p}_{1} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \cr -1 \end{bmatrix} $$
$$ \boldsymbol{p}_{2} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \cr 1 \end{bmatrix} $$
Step 2: Check for existence
Diagnoalization은 non-defective한 행렬에 대해서만 가능하다. $2 \times 2$행렬에서 두 개의 서로 다른 실수 eigenvalue를 얻었으므로 이 행렬은 non-defective하고 각 eigenvector는 선형독립이다.
Step 3: Construct the matrix $\boldsymbol{P}$ to diagonalize $\boldsymbol{A}$
Eigenvector를 구하였으므로 $\boldsymbol{P}$는 다음과 같이 간단하게 구성할 수 있다.
$$ \begin{aligned} \boldsymbol{P} &= [\boldsymbol{p}_{1}, \boldsymbol{p}_{2}] \cr &= \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \cr -1 & 1 \end{bmatrix} \end{aligned} $$
Diagonal matrix는 각 Eigenvalue이므로 $\boldsymbol{D}$는 다음과 같다.
$$ \boldsymbol{D} = \begin{bmatrix}1 & 0 \cr 0 & 3\end{bmatrix} $$
최종적으로 다음과 같이 분해할 수 있다.
$$ \begin{bmatrix}2 & 1 \cr 1 & 2\end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix}1 & 1 \cr -1 & 1 \end{bmatrix}\begin{bmatrix}1 & 0 \cr 0 & 3 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix}1 & -1 \cr 1 & 1 \end{bmatrix} $$
Properties
- Diagonal matrix $\boldsymbol{D}$는 간단하게 거듭제곱을 계산할 수 있으며 eigendecomposition을 하면 거듭제곱을 간단히 계산하는 것도 가능하다. $$\boldsymbol{A}^{k} = (\boldsymbol{PD} \boldsymbol{P}^{-1} )^{k} = \boldsymbol{P} \boldsymbol{D}^{k} \boldsymbol{P}^{-1}$$
- Eigendecomposition을 이용하면 determinant는 $\boldsymbol{D}$의 대각성분을 모두 곱해 얻을 수 있다. $$\begin{aligned} \text{det}(\boldsymbol{A}) &= \text{det}(\boldsymbol{PD} \boldsymbol{P}^{-1} ) \cr &= \text{det}(\boldsymbol{P}) \cdot \text{det}(\boldsymbol{D}) \cdot \text{det}(\boldsymbol{P}^{-1}) \cr &= \text{det}(\boldsymbol{D}) = \prod_{i} d_{ii} \end{aligned}$$ ($\boldsymbol{A}$의 determinant와 $\boldsymbol{A}^{-1}$의 determinant는 역수관계에 있다)