Chapter 4: Dynamic Programming

Dynamic programming(DP)는 MDP를 정확하게 알고 있을 때, 최적정책을 구하는 알고리즘들을 일컫는 말이다. MDP를 정확하게 알고 있다는 것은 환경에 대한 정보를 모두 알고 있다는 뜻으로 전이확률행렬(probability transition matrix)과 보상함수를 알고 있음을 의미한다. 물론 실제 강화학습 문제에서 이렇게 환경에 대한 정보를 완벽하게 알고 있는 것은 흔한 상황은 아니다. 전통적인 DP 알고리즘들은 이러한 이유로 사용에 제약이 있는 편이다. 그럼에도 불구하고 강화학습의 문제를 접근하는 중요한 이론적 토대를 제공하며 이후에 다루는 내용은 DP에서 접근하는 방식을 보다 적은 계산비용으로, 환경에 대한 정보가 완벽하지 않은 상황에서 접근하고 있다고도 할 수 있을 것이다.
이번 문서에서는 DP가 어떻게 3장에서 다루었던 value function을 계산하는데 사용할 수 있는지를 볼 것이다. 일단 optimal value function만 찾으면 optimal value function에 대해 greedy하게 행동을 한 것이 optimal policy가 되므로 이번 장에서는 Bellman optimality equation이 자주 등장하게 된다. 특히, Bellman optimality equation에서 $p(s^{\prime}, r \mid s, a)$가 포함된 꼴을 사용하게 되는데, 이 term을 사용한다는 자체가 환경에 대한 dynamics를 알고 있음을 전제로 함에 유의하며 살펴보도록 하자. 본론에 들어가기에 앞서 다음의 Bellman optimality equation을 한 번 더 확인하도록 하자.
$$ \begin{aligned} v_{*}(s)=& \max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \cr =& \max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right], \text { or } \cr q_{*}(s, a) &=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} q_{*}\left(S_{t+1}, a^{\prime}\right) \mid S_{t}=s, A_{t}=a\right] \cr &=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right)\right] \end{aligned} $$
4.1 Policy Evaluation (Prediction)
시작하기에 앞서 강화학습은 크게 정책의 평가와 정책의 학습(개선)의 단계로 나누어 볼 수 있으며 평가에 해당하는 부분을 prediction, 학습(개선)에 해당하는 부분을 control이라고 한다. 우선 임의의 정책 $\pi$를 평가하는 방법인 policy evaluation을 알아보자.
$$ \begin{aligned} v_{\pi}(s) & \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] \cr &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right] \cr &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \cr &=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} $$
상태가치는 정의에 의해 해당 상태에서 받을 수 있는 return의 기댓값이다. 여기서 중요하게 보아야 할 것 중 하나는 expectation operator의 첨자인 $\pi$이다. 특정 정책 $\pi$에 대한 평가이므로 당연히 MDP에서 $\pi$를 따르고 있음을 전제로 해야한다. 세번째에서 네번째로 넘어가는 과정은 두 가지 의미로 해석할 수 있다. 수식만 보았을 때는 기대값을 전개하는 것으로 $\mathbb{E}[X] = \sum x p(x)$에서 random variable은 $\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right]$에 대응하고 그 때의 확률은 $\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)$에 대응한다. 정책 $\pi(a \mid s)$가 정책 $\pi$일 때, 상태 $s$에서 행동 $a$를 선택할 확률이므로 직관적으로 이해할 수 있다. 계속 강조하지만 전이확률행렬인 $p$를 알고 있어야 위 식을 쓸 수 있음을 기억하자.
위 식을 바탕으로 iterative policy evaluation이라는 정책평가 방법을 사용할 수 있다.
순서대로 살펴보자. 정책을 평가하는 방법이므로 정책 $\pi$는 주어져있다고 가정한다. 그리고 정책이 수렴했는지를 확인하기 위해서 update가 일정수준 이하라면 종료하는 조건을 사용한다. 이 때, 모든 상태에서의 update되는 양의 최댓값이 threshold $\theta > 0$보다 작다면 종료한다. 상태가치 $V(s)$를 저장하기위해서 각 상태별로 상태가치의 값을 담을 수 있는 array가 준비되어야 한다. 종료상태에서의 상태가치는 $V(\text{terminal}) = 0$이다. 학습은 간단하게 이루어 진다. 우선 update양은 0으로 초기화가 된다. 그리고 각 상태별로 방문하며 현재 $V(s)$를 저장한 array의 값을 $v$로 assign한다. 여기서 update된 상태가치는 위 식에 의해 $\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right]$이다. 이 값은 $V(s)$로 assign된다. 기존에 있던 값 $v$와 현재 update한 값 $V(s)$의 차이와 이전 변화량 $\Delta$ 둘 중 최댓값이 threshold보다 작아질 때 까지 이 과정을 반복한다.
Loop의 순서를 보면 한 상태에서 계속 update를 하는 것이 아니라 모든 상태를 한 바퀴 다 돌고 다시 각각의 상태가 update된다는 점을 유의하자. 간단하게 모든상태에 대해서 한번씩 들리면서 $V(s)$를 update하고 한 바퀴를 다 돌았으면 다시 처음상태로 돌아가 동일한 과정을 반복하는 것이다. 이 과정을 반복하게 되면 $V(s)$ array가 어떤 값들로 수렴하게 될텐데 이 값들을 바로 실제 상태가치의 근사값이라고 보는 것이다. 여기서 의문이 생기는 점은 이런 iterative 방식이 수렴성과 존재성이 보장되느냐하는 것인데 결론부터 이야기하면 iterative policy evaluation 방법은 무한히 했을 때 실제 가치(하지만 주어지지 않는 한 영원히 알 수 없는) $v_{\pi}$로 수렴함이 증명되어 있다. 이로써 임의의 정책을 평가할 수 있는 도구를 얻게 되었다. 계속 강조하는 바지만 이 방법은 MDP를 알고 있을 때 평가할 수 있는 방법임을 상기하자. 증명에 관한 논의는 Stack Exchange에 언급되어 있다.
4.2 Policy Improvement
정책의 평가에 대해서 알아보았다. 궁극적으로는 정책을 평가해서 더 나은 정책을 찾는데 강화학습의 목적이 있다. 정책 $\pi$의 가치함수 $v_{\pi}$를 갖고 있다고 해보자. 임의의 상태 $s$에서 현재 정책 $\pi$를 따를지 다른 정책을 선택할지를 판단하는 기준을 생각해볼때, 행동가치함수를 생각해볼 수 있다. 행동가치에 대한 Bellman expectation equation은 다음과 같다.
$$ \begin{aligned} q_{\pi}(s, a) & \doteq \mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \cr &=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} $$
만약 어떤 행동 $a$를 선택했을 때, $q(s,a)$가 $v_{\pi}(s)$보다 크다면 현재 정책은 적어도 최적이 아니다. $a$를 선택함으로써 더 높은 기대 return을 얻을 수 있기 때문이다. 같은 논리로 모든 상태 $s$에 대해서 더 높은 $q(s,a)$를 만드는 $a$를 선택하는 것만으로도 더 좋은 정책이 된다. 이러한 논리는 policy improvement theorem에 의해 정당화된다.
두 정책 $\pi, \pi^{\prime}$이 있다고 해보자. 모든 상태 $s \in \mathcal{S}$에 대해서 $q_{\pi}\left(s, \pi^{\prime}(s)\right) \geq v_{\pi}(s)$이면 $\pi^{\prime}$은 $\pi$보다 더 좋은 정책임이 자명하다. 이에 대한 증명은 다음과 같다.
$$ \begin{aligned} v_{\pi}(s) & \leq q_{\pi}\left(s, \pi^{\prime}(s)\right) \cr &=\mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=\pi^{\prime}(s)\right] \cr &=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \cr & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, \pi^{\prime}\left(S_{t+1}\right)\right) \mid S_{t}=s\right] \cr &=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma \mathbb{E}\left[R_{t+2}+\gamma v_{\pi}\left(S_{t+2}\right) \mid S_{t+1}, A_{t+1}=\pi^{\prime}\left(S_{t+1}\right)\right] \mid S_{t}=s\right] \cr &=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} v_{\pi}\left(S_{t+2}\right) \mid S_{t}=s\right] \cr & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} v_{\pi}\left(S_{t+3}\right) \mid S_{t}=s\right] \cr & \vdots \cr & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} R_{t+4}+\cdots \mid S_{t}=s\right] \cr &=v_{\pi^{\prime}}(s) \end{aligned} $$
위 증명은 특정 상태 $s$에 대해서 전개된 것인데 같은 아이디어를 확장해서 모든 상태에서 가능한 모든 행동에 대해 $q_{\pi}(s,a)$를 최대로 하는 $a$를 선택하게 할 수도 있다. 이러한 방식을 greedy policy라고 하며 다음과 같이 표현할 수 있다.
$$ \begin{aligned} \pi^{\prime}(s) & \doteq \underset{a}{\arg \max } q_{\pi}(s, a) \cr &=\underset{a}{\arg \max } \mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \cr &=\underset{a}{\arg \max } \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} $$
이러한 방식은 이후상태를 고려하지 않아 근시안적인 정책이라고 할 수 있다. 지금의 선택이 이후에 어떻게 영향을 줄지는 고려하지 않고 당장의 행동가치가 큰 행동만 선택하기 때문이다. 딱 다음단계만 내다보고(one step of lookahead) 행동을 결정하는 것이다.
Greedy policy는 그 자체로 $q_{\pi}\left(s, \pi^{\prime}(s)\right) \geq v_{\pi}(s)$이므로 policy improvement theorem을 만족한다. 따라서 적어도 greedy policy는 적어도 현재 정책보다 비슷하거나 더 좋은 정책이다. 중요한 것은 현재 정책보다 개선된 더 좋은 정책을 찾는 것이므로 현재 정책의 가치함수에 대해 greedy하게 만듦으로써 개선할 수 있으며 이러한 방식을 policy improvement라고 한다.
새로운 greedy policy $\pi^{\prime}$이 있고 이보다 좋지는 못한 이전 정책 $\pi$가 있다고 해보자. $\pi^{\prime}$은 greedy정책이므로 다음이 성립한다.
$$ \begin{aligned} v_{\pi^{\prime}}(s) &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{\pi^{\prime}}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \cr &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi^{\prime}}\left(s^{\prime}\right)\right] \end{aligned} $$
위 식은 정확하게 Bellman optimality equation과 동일하다! 따라서 $v_{\pi^{\prime}}$은 optimal value function인 $v_{*}$여야 하며 $\pi$, $\pi^{\prime}$은 optimal policy여야 한다.
이러한 policy improvement, 즉 greedy policy를 새로운 정책으로 사용하는 방식은 기존 정책보다 좋다는 것이 보장되며 이를 사용해 정책을 개선한다는 것이 policy improvement이다.
4.3 Policy Iteration
일단 정책 $\pi$가 주어지면 정책평가를 통해 $v_{\pi}$를 구하고 이를 이용해 $\pi^{\prime}$으로 개선할 수 있다. 이는 반복적으로 사용이 가능하다. $\pi^{\prime}$에 대해서 다시 정책평가를 해서 $v_{\pi^{\prime}}$를 구하고 이를 이용해서 다시 개선해 $\pi^{\prime \prime}$으로 나아갈 수 있다. 이렇게 정책평가와 정책개선을 반복하면 최적정책(optimal policy)으로 나아갈 수 있다.
$$ \pi_{0} \stackrel{\mathrm{E}}{\longrightarrow} v_{\pi_{0}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{1} \stackrel{\mathrm{E}}{\longrightarrow} v_{\pi_{1}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{2} \stackrel{\mathrm{E}}{\longrightarrow} \cdots \stackrel{\mathrm{I}}{\longrightarrow} \pi_{*} \stackrel{\mathrm{E}}{\longrightarrow} v_{*} $$
이러한 방식으로 최적정책을 구하는 방식을 policy iteration이라고 한다. 다음의 pseudocode를 통해 구체적으로 이해해보자.
우선 상태가치에 대한 table을 초기화해준다. 정책 $\pi$도 초기에는 임의의 확률로 채워지게 된다. 이제 정책평가와 정책개선을 반복하면 된다. 정책평가는 앞의 iterative policy evaluation과 같다. 각 상태마다 들리면서 해당 생태의 상태가치를 저장하고 Bellman expectation equation으로 상태를 업데이트 한다. 그리고 상태의 변화가 사전정의한 $\theta$보다 작아질 때 까지 반복해 정책평가를 반복하게 된다. 이 과정이 끝나면 현재 정책 $\pi$에 대한 상태가치함수를 수렴시킬 수 있다. 이제 정책개선을 하면 된다. 정책개선은 간단하게 greedy하게 action을 골라주면 된다. 정책평가를 통해 이전 정책 $\pi$에서의 상태가치를 수렴시켰으므로, 각 상태를 돌면서 가장 높은 상태가치값을 갖는 다음 상태로 가는 행동을 선택하는 정책으로 update하면 된다. 이렇게 선택하는 정책이 $\pi^{\prime}$이 된다. 특히, 하나의 상태라도 이전정책과 다른 행동이 선택되었다면 policy-stable은 false로 update되고 정책평가를 update된 정책에 대해서 다시 시행하게 된다. 이 과정을 반복하며 정책 개선 이후 모든 상태에서 이전 정책과 동일한 행동이 선택되면 비로소 정책이 stable하다고 판단하고 해당 시점의 상태가치와 정책을 각각 optimal value function $v_{*}$, optimal policy $\pi_{*}$라고 판단하게 된다. 단순화 하면 다음과 같다.
- 상태가치와 정책 초기화
- 정책평가(iterative policy evaluation)
- 정책개선(greedy)
- 이전정책과 개선된 정책이 동일한 행동을 선택할 때 까지 2~3 반복
임의의 수로 채워진 상태가치와 정책에서 최적정책이 찾아지는 과정은 생각해보면 매우 신기하게 보이기도 한다. 이 신기한 과정은 속을 열고 보면 policy improvement theorem이 있기에 가능한 것이다.
4.4 Value Iteration
Value iteration은 두 가지 방법으로 이해할 수 있다. Policy iteration을 단순화 한 것과 Bellman optimality equation으로 바라보는 것이다. 하나씩 살펴보자.
Policy iteration이 갖는 단점 중 하나는 각 iteration을 구성하는 policy evaluation과 policy improvement 중에서 policy evaluation이 그 자체로 여러차례의 반복을 통해 가치를 평가한다는 것이다. Policy evaluation은 이론적으로는 무한히 반복해 정확한 정책의 가치를 수렴시킬 수 있는데 이는 현실적으로 불가능하다. 따라서 ‘적당히’ 평가하고 policy improvement로 나아가는 것이 필요하다. 여기서 다음과 같은 문제를 생각해볼 수 있다. “무한히 반복하지 않고 policy improvement를 할 때, 이러한 policy iteration은 여전히 최적정책으로의 수렴을 보장할까?”. 답은 “그렇다"이다. 이러한 성질을 극단적으로 이용하면 다음과 같은 방법을 생각해볼 수 있게 된다.
Policy iteration의 매 iteration에서 policy evaluation을 무한히 하는 것이 아닌 단 한 번만 하고 바로 policy improvement를 하는 것이다. 즉, 각 상태에 대한 평가를 한바퀴만 돌리고 이 때의 가치를 greedy하게 사용해 policy improvement를 하는 것이다. 이러한 방식을 value iteration이라고 한다.
$$\tag{1} \begin{aligned} v_{k+1}(s) & \doteq \max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \cr &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right] \end{aligned} $$
앞의 $\max_{a}$ operator자체가 의미하는 바가 greedy에 의한 policy improvement이며 뒤는 policy evaluation을 1회 iteration한 결과로 볼 수 있다. 식을 보면 Bellman optimality equation과 같음을 알 수 있다.
다른 해석방법은 Bellman optimality equation의 관점으로 바라보는 것이다. 임의로 초기화 된 가치에서 출발해 Bellman optimality euqation을 이용해 최적가치를 수렴시켜가는 것이다. 물론 이러한 접근은 MDP의 정보, 특히 보상함수와 전이확률행렬을 알기에 가능하다. 이러한 방식으로 접근하면 정책이 주어지지 않은 상태(임의로 초기화 된 가치함수의 greedy)에서 가치함수를 수렴시킬 수 있다. 그리고 iteration에서 가치함수의 차이가 사전에 정한 threshold이하로 내려간다면 종료하는 조건으로 계속 반복하면 가치함수를 수렴시킬 수 있다. 이 상태에서 greedy한 선택을 하면 최적가치함수에 대한 greedy이므로 여기서의 greedy는 그 자체로 optimal policy가 된다.
Pseudocode를 살펴보자.
수렴여부를 결정할 threshold를 충분히 작은 값으로 설정하고 가치함수 $V(s)$를 임의의 값으로 초기화한다. 이후 policy evaluation에 해당하는 loop를 돌게 되는데 각각의 상태를 방문하며 Bellman optimality equation을 사용해 가치함수를 추정한다. 여기서 눈여겨볼 점은 policy improvement없이 threshold조건을 만족할 때 까지 계속 반복하는 것이다. 이는 high-level에서 생각해보면 agent가 실제 행동을 하는 것이 아닌 머리속으로 가능한 결과들을 simulation해보면서 최적의 정책을 찾는 과정이다. MDP를 알고 있다고 가정했을때 사용 가능한 방식이므로 실제 환경과의 상호작용이 필요하지 않다. 식에서 $p$를 사용하고 있음에 유의하자. 이렇게 가치함수를 수렴시키게 되면 이 가치함수에 대해서 greedy하게 행동을 고르는 방식인 $\pi(s)=\arg \max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma V\left(s^{\prime}\right)\right]$이 최적정책이 된다.
언급한 대로 policy iteration처럼 policy evaluation을 무한히 수렴시키는 것이 아닌 policy evaluation과 policy improvement를 각각 one sweep으로만 평가, 개선하므로 수렴속도가 빠르다.
4.5 Asynchronous Dynamic Programming
DP 방식의 단점은 MDP의 전체 상태에 대해서 방문하는 과정(sweep)이 필요하다는 것이다. 복잡한 문제일 수록 MDP의 상태공간은 이렇게 하나하나 방문하기에는 너무도 크다는 문제가 생기게 된다. Asynchronous DP 방법은 일반적인 DP방법과는 다르게 각각의 상태를 모두 거쳐가지 않아도 되는 in-place iterative DP 방식이다. In-place는 table에 값을 update할 때 해당 위치를 덮어써버리는 방식으로 생각하면 된다. 기존에는 별도의 변수에 저장을 해두고 update를 할 때 assign을 해주었다면 in-place에서는 table 값 자체를 바로 바꾸어 버리기 중간에 저장하기 위한 별도 변수를 사용할 필요가 없다는 장점이 있으나 update에 참조하는 위치가 update를 할 위치라는 점 때문에 불안정할 수 있다는 단점도 있다. Asynchronous DP의 특징은 그 이름에서 나타나듯 비동기적이라는 것이다. 일반적인 DP가 순차적으로 상태를 방문했다면 asynchronous DP는 임의의 순서로 방문할 수도 있고 one sweep을 돌기전에 이미 방문한 상태들을 미리 update하는 것도 가능하다. 물론 올바르게 수렴하기 위해서는 asynchronous DP라고 해도 모든 상태들에 대해서 update가 이루어져야 한다. 완벽하게 비동기적인 아닌 이유는 임의의 순서로 방문해 update하더라도 일정 수준에서는 모든 상태를 방문해야만 계산이 가능한 경우도 발생하기 때문이다. 그럼에도 불구하고 asynchronous DP가 갖는 의의는 update할 상태를 고르는데 유연성을 제공한다는데 있다.
Asynchronous DP의 예로 asynchronous value iteration을 알아보면, 이 방법은 가치함수를 update할 때 모든 상태를 도는 sweep을 하는 것이 아닌 각각의 step $k$의 상태 $s_k$에 대해 (1)을 사용해서 즉시 가치함수를 update한다. 그렇다고 모든 상태 sweep을 하지 않아도 수렴이 보장된다는 건 아니다. $0 \leq \gamma < 1$일 때, 모든 상태들을 무한히 많이 반복할 때에 한해서 점진적으로 최적가치인 $v_{*}$로 수렴하는 것이 보장된다. 따라서 sweep을 꼭 순서대로 돌지 않고 유연하게 update할 수 있다는 것일 뿐 모든 상태들에 대해서 update가 이루어지지 않으면 수렴은 보장되지 않는다. 비슷한 방식으로 앞의 policy evaluation과 value iteration을 섞은 policy iteration 방법도 생각해 볼 수 있다. Policy iteration은 policy evaluation과 policy improvement를 반복적으로 거치는데 이 때 policy evaluation을 여러차례 수렴시키지 않고 1회의 sweep만 한 것이 value iteration임을 확인했었다. 이 때 evaluation 부분에서 asynchronous value iteration을 도입함으로써 policy evaluation을 비동기적으로 하는 방법을 떠올려 볼 수 있을 것이다. 특히, 비동기의 장점을 활용해 분산학습을 시키는 것도 가능하므로 stochastic하게 모든 상태에 대해서 분산시켜 학습한다면 어찌되었든 모든 상태에 대해서 평가를 해야한다는 제약을 보다 잘 만족시킬 수 있을 것이다. 이런 방식을 사용하게 되면 특히 sweep이 굉장히 오래걸리는 문제에 대해서 빠르게 policy evaluation과 policy improvement 단계를 진행할 수 있기 때문에 유용하게 사용할 수 있다. 그리고 많은 경우 모든 상태가 동일하게 중요하지는 않으므로 더 중요한 상태들에 대해 더 자주 update를 진행하는 방법 등을 활용할 수 있는 여지도 생기게 된다.
4.6 Generalized Policy Iteration
앞서 다룬 policy iteration은 정책평가와 정책개선을 번갈아가며 수행해 최적정책을 찾는 방식이다. 정책개선작업을 시작하기 위해서는 앞선 정책평가가 끝나기를 기다려야 하고 정책 평가를 하기 전에는 정책개선이 마무리되기를 기다렸다가 시작해야한다. 하지만 generalized policy iteration은 이러한 과정에 대해 “반드시 번갈아가면서 수행해야만 할까?“라는 물음에서 출발한다. 당장 value iteration만 보더라도 정책평가는 단 한 번이루어지며 그 다음부터는 Bellman optimality equation을 사용해 바로 정책 개선에 들어간다. Asynchronous DP에서는 sweep하는 방식도, update하는 시점도 on the fly로 했었다. 어떻게든 평가와 개선이 모든 상태들에 대해서 계속 이루어진다면 최종적으로는 최적가치함수나 최적정책으로 갈 수 있다.
이렇게 정책평가와 정책개선이 상호작용의 관점에서 바라보는 것을 generalized policy iteration (GPI) 라고 한다. 이 때 각 방식의 자잘한 세부사항들과는 독립적으로 보는 관점을 갖는다. 책에서 다루고자 하는 요점은 정책평가와 정책개선은 각각 policy, value function의 관계로 서로 영향을 주고 받는다는 내용이다. 앞서, 최적가치함수에서의 greedy는 그 자체로 최적정책이 된다는 것과 Bellman optimality equation와 같은 맥락이다. 따라서 정책함수와 가치함수는 서로 영향을 계속 주고 받게 된다.
정책평가와 정책개선은 내재적으로 경쟁하고 협력하는 관계로 볼 수 있음을 제시한다. 정책을 가치함수에 대해서 greedy하게 잡으면 greedy한 정책은 가치함수를 부정확하게 만들게 되고 가치함수를 정책에 대해서 많이 변하지 않게 한다면 정책을 greedy하게 쓰기 어렵게 된다. 정책개선단계는 greedy하게 가치함수를 exploit하려고 할 것이고, 정책평가는 현재 정책을 사용해 가치함수를 수렴시키려 할 것이다. 학습과정에서 이 둘은 각자 단계에서의 목적을 달성하려고 하며 이 때 찾아지는 타협점이 최적가치함수, 최정정책이 된다는 관점으로도 볼 수 있다.
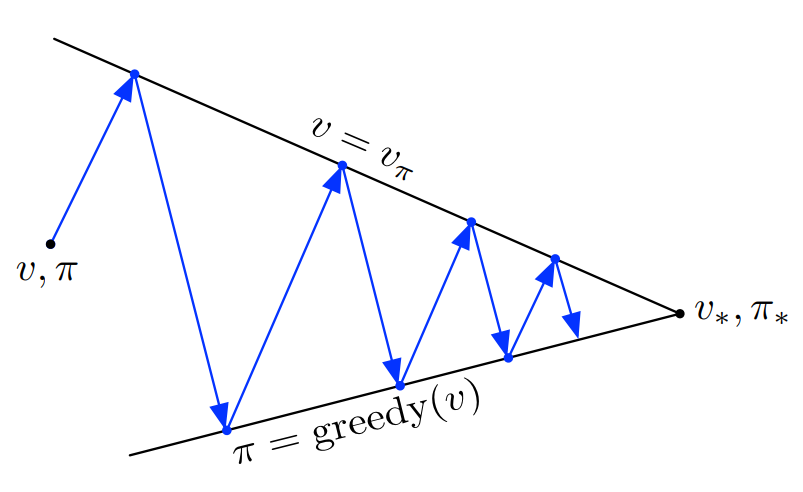
또 다른 관점은 GPI의 정책평가와 정책개선을 각각의 제한조건 또는 목표로 볼 수 있다. 위의 그림처럼 최적가치함수와 최적정책으로 수렴시키기 위해서 가치함수의 방향과 정책의 방향은 서로 작용하며 최적점으로 나아갈 수 있게 해준다. 각각의 화살표는 policy iteration으로 해석할 수 있다.
4.7 Efficiency of Dynamic Programming
DP방식은 일반적으로 큰 규모의 문제를 푸는데 적합하지 않지만 다른 MDP solver에 비교하면 효율적인 편이다. DP방법을 최적정책을 찾는데 필용한 worst case time은 상태와 행동의 다항식꼴로 표현되게 된다. 상태의 개수는 $n$ 행동의 개수를 $k$라고 할때, DP방법은 $k^{n}$개인 전체 정책에 대해서 최적정책을 찾을 수 있음이 보장되어 있다. Linear programming으로도 MDP를 풀 수는 있지만 DP보다 훨씬 적은 상태개수에 대해서도 현실적으로 풀기가 어려워지며 규모가 커지는 경우에는 사실상 DP만이 유일한 선택지가 된다. DP는 차원의 저주(curse of dimensionality)로 인해 사용에 제한이 있는 것으로 여겨지지만 이는 문제 자체가 갖는 어려움이지 DP에 국한된 문제만은 아니다. DP는 direct search나 linear programming에 비해서는 분명 큰 문제들에 접근하기 좋은 방식이다.
실제로 오늘날 향상된 계산성능을 활용해 규모가 큰 MDP문제들을 풀어내고 있으며 앞서 언급된 DP는 교과서에만 언급된 방법이 아닌 현역으로 사용되는 알고리즘들이다. Policy iteration이나 valute iteration은 어느 하나가 일반적으로 좋다고 말하기는 어렵지만, 두 방식 모두 이론적인 worst-case run time보다 빨리 최적정책으로 수렴하는 경향을 보이며 특히 좋은 초기상태에서 시작할 경우 이런 경향은 두드러진다.
상태공간이 큰 문제들에 대해서는 asynchronous DP방식이 선호된다. 상태가 커질수록 정책평가를 위한 one sweep의 비용도 비례해서 커지게 된다. 지금 다루는 part는 tabular method라는 점을 상기하자. 상태공간이 커지면 table의 크기도 커지게 되고 synchronous방식에서는 table의 모든 행을 한 바퀴 돌아야 sweep이 끝나는 것이다. 다만, 문제를 푸는데 모든 상태가 동등하게 중요하지는 않으므로 최적정책에 필요한 상태들을 비교적 정확하게 추정했다면 규모가 큰 MDP도 풀 수 있는 가능성이 열려있다. 이러한 경우에는 asynchronous 방식이나 GPI의 variants를 활용해서 synchronous 방법보다 충분히 좋은 정책을 빠르게 찾아낼 수 있게 된다.
4.8 Summary
이번 문서에서는 finite MDP를 푸는 방법으로서의 dynamic programming 방법들을 알아보았다.
Policy evaluation은 주어진 정책을 사용해서 가치함수를 반복적으로 추정하는 방식이며 policy improvement는 주어진 가치함수를 사용해서 정책을 개선하는 것으로 가장 쉬운 방식으로는 greedy policy가 있다. 이 둘을 순차적으로 사용하게 되면 policy iteration이나 value iteration의 방법이 된다.
Classical DP 방법에서는 모든 상태를 방문하는 sweep을 수행하면서 update를 하게된다. 이 과정에서 수행하는 update는 Bellman expected/optimality equation을 사용하게 되며 이는 backup diagram과 같이 보면서 이해하는 것이 많은 도움이 된다.
거의 대부분의 강화학습 방법은 정책평가와 개선단계가 포함되므로 일반적인 관점에서 정책반복법으로 생각해볼 수 있고 이러한 관점을 generalized policy iteration(GPI)로 다루었다. GPI는 특정한 알고리즘을 지칭하는게 아니라 개념/관점이다 보니 정책과 가치함수를 번갈아 추정하며 나아가는 개념으로 이해하도 괜찮을 것이다. 정책평가 단계에서는 평가할 정책이 고정되고 해당 정책을 사용해 가치를 평가하며 정책개선 단계에서는 가치함수가 고정되고 이를 통해 정책을 개선해 나아가게 된다.
DP 방법에는 꼭 sweep을 완전하게 돌면서 update하는 방식 이외에도 비동기적으로 학습하는 asynchronous DP이 있음을 보았다. Asynchronous DP에서는 sweep을 완전히 돌지도, 순서대로 돌지도 않는다.
DP방법의 성질 중 하나로 추정치로 추정치를 update하는 bootstrapping이라는 방법이 있다. 그리고 booststrapping은 MDP를 완전히 알고있음을 가정하는 DP방식이 아닌 경우(model-free)에도 사용하는 방법으로 이후에 자세히 다루게 된다.