Chapter 3: Finite Markov Decision Process

이 문서에서는 finite Markov decision process(finite MDP)에 대해 다룬다. 어떤 문제를 풀기 위해서는 다루려는 문제를 어떻게 바라보고 접근할지를 정해야 한다. 강화학습을 공부할 때 MDP가 반드시 등장하게 되는 이유는 강화학습이 다루는 문제를 MDP로 접근하기가 용이하기 때문이다. MDP는 강화학습이 다루는 순차적 의사결정 문제를 잘 표현하는 것은 물론 지연보상과 같은 강화학습 문제의 특징도 잘 통합해 다룰 수 있는 토대를 제공한다. Bandit 문제에서처럼 evaluative feedback을 반영하는 상황과 다른 상황에서 다른 행동을 취해야 하는 associative문제 모두 MDP를 이용해 표현이 가능하다.

Bandit 문제에서는 상태라는 것이 처음에 보는 화면이외의 상태라고 할만한 것이 없었기에 가능한 $a$에 대해 $q_{*}(a)$를 잘 추정하는 문제로 한정되었었다. 하지만 일반적인 강화학습 문제는 다양한 상황이 존재한다. MDP는 이처럼 상황이 한 번에 종료되는 것이 아닌 연속적인 상황을 다루는데 적절하며 최적의 방법을 찾기 위해 MDP에서는 상태 $s$에서 행동 $a$에 대한 행동가치 $q_{*}(s, a)$를 추정하거나 최적의 행동이 주어졌을 때의 상태가치 $v_{*}(s)$를 추정하게 된다. 둘 다 상태에 의존함을 알 수 있는데, 이는 각각의 행동에 대한 장기적인 결과를 적절하게 추정하기 위한 필연적인 성질이다.

이번 chapter에서는 MDP가 강화학습의 문제를 어떻게 수학적으로 표현하는지를 다루고 그 과정에서 return, 가치함수, Bellman equation에 대해서 다루게 된다. MDP도 인공지능의 다른 접근방법처럼 적용할 수 있는 범위와 수학적 tracktability가 trade-off관계에 있다. 풀어 말하자면, 더 넓은 범위에 적용하려고 하면 수학적으로 tractable해지지 않고, 수학적으로 tractable한 접근을 하려면 문제의 범위를 제한해야한다는 trade-off가 있게 된다. 이번 chapter에서는 이러한 trade-off와 이로인한 어려움 점들에 대해서도 논의한다. MDP를 벗어나는 강화학습은 교재 chapter 17에서 다룬다.

3.1 The Agent-Environment Interface

MDP는 강화학습처럼 환경과 상호작용하며 목적을 달성해야 하는 문제를 다루는데 적합한 토대를 제공한다. 학습하고 행동을 결정하는 주체를 agent라고 하며, agent가 상호작용 하는 대상을 환경(environment)라고 한다. 환경이 꼭 물리적으로 외부에 존재할 필요는 없다. Agent기준으로 외부에 있는 것은 모두 환경이라고 할 수 있다.

Agent가 상태를 바탕으로 어떤 행동을 하게되면 환경은 해당 행동에따른 변화된 상태와 보상을 제공한다. 그리고 agent는 이 정보를 바탕으로 다음의 행동을 이어가게 된다.

순서상 닭이 먼저냐 달걀이 먼저냐 문제가 되지만 일반적으로 어떤 상태를 보고 취한 행동을 같은 time step으로 간주한다. 풀어서 설명하면 위 상호작용이 time step $t = 0, 1, 2, 3, \ldots$와 같이 발생한다고 할 때, 특정 $t$에서 agent는 환경의 상태 $S_t \in \mathcal{S}$를 보고 행동 $A_t \in \mathcal{A}(s)$를 선택한다. 그러면 그 결과로 다음 time step $t+1$에서 보상 $R_{t+1} \in \mathcal{R} \subset \mathbb{R}$과 함께 새로운 상태 $S_{t+1}$을 보게 된다. 이러한 일련의 과정을 trajectory라고 하며 순서대로 쓰면 다음과 같다.

$$S_{0}, A_{0}, R_{1}, S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, R_{2}, \ldots$$

여기서는 finite MDP만을 다룬다. 즉, MDP에서 가질 수 있는 상태, 행동으 그리고 보상의 수는 모두 유한하다. Finite MDP를 가정하면 이전 상태와 행동으로부터 현재의 보상과 상태에 대한 이산확률분포를 갖게된다. 즉 다음을 정의할 수 있게 된다.

눈여겨볼점은 이렇게 정의된 함수 $p$이다. $p$는 MDP가 어떻게 작동하는지를 결정하게 된다. MDP가 작동하는 방식에 대해 포괄적으로 dynamics라고 하며, 따라서 $p$가 MDP의 dynamics를 정의한다고 표현할 수 있다. 위 식에도 definition 기호인 $\doteq$를 사용하고 있다. $p$는 네개의 인자를 갖는 함수로 $p: \mathcal{S} \times \mathcal{R} \times \mathcal{S} \times \mathcal{A} \rightarrow [0, 1]$이다. 식에 있는 $\mid$ 기호는 조건부확률처럼 자연스럽게 해석할 수 있다. 강화학습의 dyanmics식에서 $\mid$는 $\mid$ 뒤의 “상태와 행동을 선택했을 때"를 의미한다.

$$ \sum_{s^{\prime} \in \mathcal{S}} \sum_{r \in \mathcal{R}} p\left(s^{\prime}, r \mid s, a\right)=1, \text { for all } s \in \mathcal{S}, a \in \mathcal{A}(s) $$

이를 좀 더 자세히 알아보자. MDP는 다음과 같은 정보를 사용한다.

$$MDP \coloneqq (\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma)$$

이후에 반복해서 언급하겠지만 이쯤에서 MDP를 안다라는 의미에 대해 생각해보자. 결론부터 이야기하면 MDP를 안다는 것은 위의 모든 인자들을 안다는 것이다. 상태와 행동은 agent입장에서 관측하고 결정하는 행동이므로 agent가 알 수 있다. 그렇다면 전이확률과 보상함수는 어떨까? 현재 상태에서 특정 상태로 갈 확률 그리고 현재 상태에서 특정 행동을 했을 때의 보상은 agent가 아닌 환경이 결정하는 영역이다. 문제의 성질에 따라 agent가 환경에 대한 정보를 알 수도 모를수도 있게 되는데 환경에 대한 정보, 즉 환경에 대한 모델을 알고 있다면 model-based가 되는 것이고 환경에 대한 모델을 모른다면 model-free가 되는 것이다. 정리하면 model-based의 경우 MDP에 대해 완전히(complete) 알고 있을 때 가능한 방식이다. 세부적인 내용은 이후에도 반복되므로 여기서는 MDP를 안다는 것은 위의 모든 인자들을 안다는 것을 의미한다 정도로 이해하는 것으로 충분하다.

그리고 MDP에서 중요한 것이 Markov property이다. 내용은 간단하다. 어떠한 상태가 과거의 모든 agent-environment interaction을 갖고 있다면 이는 Markov property를 만족한다고 한다. 다음상태, 즉 미래는 현재상태에만 의존하지 다음상태를 결정하는 함수는 현재상태이외의 과거상태에 의존하지 않는다는 의미이다. MDP는 기본적으로 Markov property를 만족한다.

Markov property에서 자주 발생하는 오해가 바로 상태와 시점의 구분이다. 꼭 현재 상태가 하나의 시점으로 구성될 필요는 없다. 대표적으로 Atari게임으로 유명한 DQN의 경우 이전 4개의 프레임을 하나의 상태로 구성하였다. 따라서 시점과 상태를 동일하게 생각하지 않도록 주의하자.

위의 Four-argument Dyanimcs Function에서 보상에 대해 summation하면 다음의 state-transition probabilities $p: \mathcal{S} \times \mathcal{S} \times \mathcal{A} \rightarrow [0, 1]$를 얻을 수 있다.

$$ \begin{aligned} p\left(s^{\prime} \mid s, a\right) &\doteq \operatorname{Pr} \left\lbrace S_{t}=s^{\prime} \mid S_{t-1}=s, A_{t-1}=a\right\rbrace \cr &= \sum_{r \in \mathcal{R}} p\left(s^{\prime}, r \mid s, a\right) \end{aligned} $$

State-action pair로 표현되는 two-argument 보상함수 $r: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$는 다음과 같이 정의된다.

$$ \begin{aligned} r(s, a) &\doteq \mathbb{E}\left[R_{t} \mid S_{t-1}=s, A_{t-1}=a\right] \cr &= \sum_{r \in \mathcal{R}} r \sum_{s^{\prime} \in \mathcal{S}} p\left(s^{\prime}, r \mid s, a\right) \end{aligned} $$

State-action-next-state triples로 표현되는 three-argument 보상함수 $r: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow \mathbb{R}$는 다음과 같이 정의된다.

$$ \begin{aligned} r\left(s, a, s^{\prime}\right) &\doteq \mathbb{E}\left[R_{t} \mid S_{t-1}=s, A_{t-1}=a, S_{t}=s^{\prime}\right]\cr &= \sum_{r \in \mathcal{R}} r \frac{p\left(s^{\prime}, r \mid s, a\right)}{p\left(s^{\prime} \mid s, a\right)} \end{aligned} $$

대부분의 경우 Four-argument Dyanimcs Function으로 표현하기도하고 나머지는 쉽게 유도가 가능하므로 Four-argument Dyanimcs Function정도는 암기하는 것이 좋다.

MDP는 순차적 의사결정 문제에 대해 유연하게 적용할 수 있다. 책의 다음 문장이 이를 깔끔하게 설명한다.

In general, actions can be any decisions we want to learn how to make, and the states can be anything we can know that might be useful in making them.

학습하기를 바라는 결정과정은 무엇이든 행동으로 취급할 수 있으며 그러한 행동을 위해 필요한 유용한 정보는 무엇이든 상태로 취급할 수 있다. 또한 agent와 환경의 구분이 꼭 물리적인 내부와 외부로 나누어지는 것은 아니므로 혼동될 수 있는데, 일반적으로 다음의 기준을 사용하면 구분이 용이하다.

Agent가 마음대로 변경할 수 없는 것들은 환경의 일부로 간주한다.

MDP는 상호작용이 있는 목표지향적(goal-directed) 학습문제에 대한 framework를 제공한다는 의의가 있다. Agent와 환경이 상호작용하며 목적을 달성해야 하는 상황을 상태와 행동, 전이확률과 보상함수에서의 신호교환이라는 형태로 추상화하는 도구를 제공해 이후에 다룰 다양한 도구들을 사용할 수 있는 토대를 마련해준다.

3.2 Goals and Rewards

강화학습의 목표는 간단하다. Agent가 return을 최대로 받게 하는 것이다. 강화학습에서의 보상은 하나의 숫자이다. 각각의 시점에서의 보상은 스칼라값 $R_t \in \mathbb{R}$로 표현할 수 있다. 그런데 복잡한 작업에 대해서도 고작 하나의 스칼라 값인 보상을 사용할 수 있을까? 더 복합적인 정보를 표현할 수 있도록, 예를 들어 “보상의 집합으로 구성해야 하지 않을까?“라는 생각을 해볼 수 있다. 결론은 그렇게 해야한다는 것이다. 보상신호가 복잡해지게 되면 학습과정은 훨씬 어려워지게 된다. 따라서 강화학습은 reward hypothesis라는 가정을 전제로 한다.

굉장히 당연한 이야기지만 동시에 중요한 가정이다. 강화학습은 MDP를 사용해 표현하고 MDP에서 학습방향은 보상에 의해 정의가 된다. 따라서 expected return을 최대화하는 방향이 우리가 풀고자하는 문제의 방향을 나타내어야 원하는 결과를 얻을 수 있다. Reward hypothesis는 이러한 기본전제를 명시적으로 표현해준다.

또한 보상설정에서 매우 중요한 부분은 보상은 달성하고자 하는 목적 그 자체가 되어야지 달성하는 방법에 관한 것이 되어서는 안된다.

The reward signal is your way of communicating to the robot what you want it to achieve, not how you want it achieved.

실제로 강화학습 문제에서 보상설계는 그 자체로 매우 어렵고 중요한 부분이다. 관련해서, 자주 하게 되는 실수 중 하나가 보상을 사전지식(prior knowledge)을 넣기 위한 수단으로 사용하는 것이다. 교재의 예처럼 보상은 이길 때 주어지는 어떤 양수값이 되어야지, 퀸이라는 말을 잡는 것이 보상이 되어서는 안된다. 만약 이렇게 설계한다면 게임을 지더라도 퀸을 잡는 원치 않은 결과를 얻게 될 수 있다. 따라서 보상은 원하는 목적 그 자체를 표현해야지 어떤 문제의 subgoal을 달성하도록 설정되어서는 안된다.

물론, 보상을 통해서 사전지식을 넣는게 잘못된 것이지 사전지식을 주입하는 자체가 틀린 것은 아니다. 실제로, AlphaGo는 프로기사들의 대국을 사전정보로 사용하였다. 단계적으로 목적을 달성하도록 하는 curriculum learning이라는 방법도 있다. 다만, 두 방식 모두 보상으로 사전지식을 주입하지는 않는다.

3.3 Returns and Episodes

강화학습의 목적을 이야기하면서 보상과 return에 대한 언급이 있었다. 보상은 매 time step $t$마다 환경에 의해 주어지는 스칼라 값을 갖는 신호이다. 따라서 $R_{t}, R_{t+1}, R_{t+2}, \ldots$와 같이 표기된다. 종종 강화학습의 목적이 보상을 크게한다고 표현하는 경우가 있는데, 엄밀한 의미에서 이는 틀린 문장이다. 보상은 하나의 신호에 불과하다. 강화학습을 통해서 달성하고자 하는 것은 expected return을 최대로 하는 것이다. 즉, return의 기댓값을 최대화 하겠다는 건데 그렇다면 return의 정의를 알아보자.

상당히 추상적으로 정의되어있지만 이는 return이 하나의 식으로 정해져있는 것이 아니기 때문이다. 가장 간단한 형태의 return을 예로 보자.

$$G_{t} \doteq R_{t+1} + R_{t+2} + R_{t+3} + \cdots + R_{T}$$ $T$는 마지막 time step이다.

위의 return은 단순하게 이후에 받을 보상의 합이다. 여기서 $T$, final time step에 대해 생각해보자. 강화학습은 순차적 의사결정 문제를 다룬다. 여기서 문제는 끝이 있는 문제일까? 문제에 따라 그럴수도, 그렇지 않을 수도 있다.

Agent-environment interaction이 subsequence로 쪼개질 수 있다면 이 subsequence를 episode라고 한다. 대표적인 것이 게임이다. 게임의 한 판이 하나의 episode인 것이다. 바둑이라는 게임은 엄청난 숫자의 경우의 수와 전략이 존재한다. 하지만 학습을 할 때는 대국단위로 쪼개서 학습을 하게 된다. 수 많은 대국을 통해 학습하겠지만 하나의 subsequence인 대국 한 판이 episode에 해당하는 것이다. 그리고 episode의 가장 마지막 상태를 terminal state라고 한다. Terminal state에 도달하게 되면 다시 초기상태로 돌아가게 된다. 통계적인 관점에서 보면 한 episode가 끝나고 다른 episode가 되는 것은 다른 독립사건이 발생하는 것이다. 이전 episode에서 졌던 이겼던 다음 게임과는 상관이 없다. 이렇게 episode로 나누어질 수 있는 문제를 episodic task라고 한다. Episodic task에서 마지막 terminal state를 구분하기 위해 nonterminal state를 $\mathcal{S}$로, terminal state를 $\mathcal{S}^{+}$로 표기한다. 마지막 time step인 $T$는 각 episode마다 달라질 수 있는 값으로 random variable이다.

그렇다면 episodic task가 아닌 문제를 생각해보자. 모든 문제가 꼭 끝이 있지는 않다. 지속적으로 작업하는 로봇을 생각해보면 작업의 끝이 명시적으로 정해져 있지 않음을 알 수 있다. 일이 들어오는대로 계속해야하는 것이다. 이러한 작업을 continual task라고 한다. 여기서 문제가 생긴다. $T = \infty$가 되면서 갑자기 앞에서 정의한 return이 무한급수(infinite series)가 되어버렸다. 따라서 단순합으로 정의한 앞의 return도 무한대의 값을 가질 수 있다. 이렇게 되면 expected return을 최대화 하는 것은 무한대를 최대화하는 것으로 수학적으로 맞지 않고, 무한대의 시간을 활용해서 달성하는 것은 유용하지도 않다. 따라서 자연스럽게 discounting이라는 개념을 도입하게 된다.

Discounted return은 은행의 복리이자와 완전히 같은 개념이다. 내년의 돈의 가치를 올해로 환산하기 위해서는 물가상승분에 대한 discount를 해주어야 한다. 내후년에는 2년이 물가상승분만큼의 discount를 해야한다. 따라서 이후에 가지고 있을 돈을 현 시점에서 환산한다면 미래의 돈은 현재로부터 떨어진 만큼 discount를 많이 해야하는 것이다.

강화학습의 문맥에서 $\gamma = 0$으로 본다면 오직 현재의 보상만 높게하는 근시안적인 agent가 될 것이고 $\gamma = 1$에 가까워진다면 미래의 보상값을 더 강하게 고려하는 장기적인 관점의 학습을 하는 agent가 될 것이다.

Return은 다음과 같이 time step에 대해 recursive하게 나타낼 수 있다.

$$ \begin{aligned} G_{t} & \doteq R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} R_{t+4}+\cdots \cr &=R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\gamma^{2} R_{t+4}+\cdots\right) \cr &=R_{t+1}+\gamma G_{t+1} \end{aligned} $$

또한 $\gamma$가 $\gamma < 1$인 상수이고 보상이 매 time step마다 1이라면 다음과 같이 수렴한다.

$$ G_{t}=\sum_{k=0}^{\infty} \gamma^{k}=\frac{1}{1-\gamma} $$

3.4 Unified Notation for Episodic and Continuing Tasks

앞에서 강화학습의 task를 분류하는 다양한 방법 중 episodic task와 continuing task로 구분하는 방법을 알아보았다. 이제 앞으로 다룰 강화학습 내용을 일관성있게 전개하기 위해 두 가지 경우 모두에 대해 사용할 수 있는 return의 표기법을 정의해보자.

강화학습은 표기법에 있어서 다양한 상황을 반영해야하므로 이것저것 많이 붙게되는데 논문을 읽을 때 이러한 convention에 익숙하지 않으면 무슨소리인가 싶을 때가 많아지므로 표기법 자체도 유의해서 살펴보아야 한다. 예를 들어, 지금까지 상태는 $S_{t}$로 표현해왔다. 하지만 time step $t$는 다양한 episode에서 존재할 수 있으므로 엄밀하게 $i$번 째 episode의 time step $t$를 지칭한다면 $S_{t, i}$와 같이 표기해야한다. 하지만 다행(?)스럽게도 대부분의 경우 문맥상 하나의 episode내에서 이야기를 하기 때문에 episode를 직접 표기하는 일은 거의 없다. 따라서 앞으로도 특정 episode의 time step $t$는 편의상 $S_{t}$로 표기한다. 강화학습에서는 엄밀하게 super/sub script를 모두 쓰면 붙는게 너무 많아서 이런 식의 편의상 생략이 자주 일어나는 편이다.

다음으로 episodic task와 continuing task를 구분하지 않고 하나의 표기법을 사용하기 위해서는 두 task를 하나의 task로 표현하는 것이 먼저이다. 특성상 무한히 진행될 수 있는 continuing task를 episodic task의 형태로 바꾸는 것은 불가능하다. 하지만 다음과 같이 바라보면 반대는 가능하다.

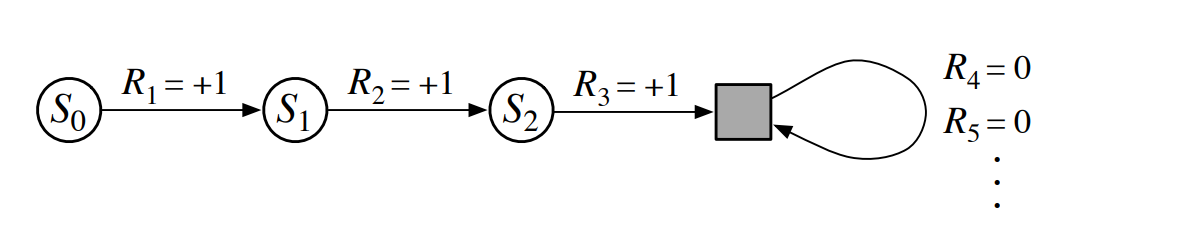
Episodic task에 대해서 위의 회색 박스로 표현된 absorbing state라는 특수한 상태를 사용해 continuing task처럼 처리할 수 있다. Absorbing state는 0의 보상을 반환하면서 자기 자신의 상태로 돌아오는 상태이다. 이러한 성질은 discounting이 있는 상황에서도 그대로 사용할 수 있다는 이점을 갖는다.

따라서 이제 두 가지 task 모두에 적용할 수 있는 return을 다음과 같이 쓸 수 있다.

$$G_{t} \doteq \sum_{k=t+1}^{T} \gamma^{k-t-1} R_{k}$$

이 때, $T=\infty$이거나 $\gamma=1$일 수 있으나 둘 다여서는 안된다.

이제 문서 전반에 걸쳐서 위 형태의 return식을 사용한다.

3.5 Policies and Value Functions

강화학습의 목표는 최적정책(optimal policy) 또는 최적가치함수(optimal value function)을 찾는 것이다. 강화학습에서 핵심개념인 정책과 가치함수에 대해 다루어보자. 이 둘은 강화학습을 공부하는데 있어서 가장 중요한 개념들로 교재공부할 때 필요한 것은 물론, 정확히 알아야 강화학습 알고리즘과 관련된 논문을 읽을 수 있다.

가치함수이 $v_{\pi}$와 $q_{\pi}$는 정책 $\pi$를 따르는 trajectory를 통해 경험으로 학습할 수 있다. 앞으로도 여러차례 강조될 내용이지만 강화학습에서 기대값 연산자는 매우 중요한 역할을 담당한다 위의 상태가치나 행동가치도 기대값으로 표현되어있는데 이는 기대값 연산자 안의 항 각각은 정학한 estimate이 되지는 않지만 이들의 평균은 unbiased estimate이 된다는 것을 의미한다. 다시 말해, sample기반 방법을 사용할 수 있게 해주는 중요한 연산자이다.

이렇게 실제 관측한 sampling된 결과들을 평균을 내서 추정하는 과정을 Monte Carlo methods라고 한다. Monte Carlo methods는 5장에서 다루게 된다. 여기서 MDP가 작다면 표의 형태로 작성해 각 상태에서 받은 return을 기록해 Monte Carlo를 적용할 수 있겠지만 MDP가 크다면 불가능하다. 상태도, 행동도 많다면 특정 상태에서 특정행동을 하는 것 자체가 매우 희소하므로 이론적으로 가능하더라도 현실적으로 불가능한 경우가 많다. 따라서 MDP가 클 때는 $v_{\pi}$나 $q_{\pi}$를 parameterized function으로 잡고 이 함수를 학습시키는 방법을 사용하게 되는 것이다. Parameterized function으로 neural network를 사용한 것이 Deep RL이다. 이 parameterized function을 function approximator라고도 부른다. 책의 Part I은 tabular method로 지금 말한 경우 중 MDP가 작은 경우이다. 따라서 표에 기록하면서 필요한 값들을 추적할 수 있다. MDP가 커져서 이런 방법이 불가능한 경우가 책의 Part II에서 다루는 내용이다.

가치함수의 중요한 특징 중 하나는 recursive하게 표현이 된다는 것이다. 그리고 이는 dynamic programming, 즉 문제를 작은 문제들로 나누어 푼다는 측면에서 매우 유용한 성질이다. 가치함수는 여러가지의 표현형을 갖는데, 특히 Bellman equation으로 표현되는 표현형은 모두 외워두면 이후 과정을 이해하는데 매우 편리하다.

첫 번째 줄은 그 자체로 상태가치의 정의이다. 그리고 return의 recursive형태로 바꾸어 준 것이 두번째 줄이다. 그 다음부터는 기대값을 전개하는데 가중평균으로 보면 된다. 두번째에서 세번째줄로 가는 과정은 다음을 순차적으로 대입하면 쉽게 이해가 된다.

$$ \begin{aligned} v_{\pi}(s) &= \sum_{a \in \mathcal{A}} \pi (a \mid s) q_{\pi}(s, a)\cr q_{\pi}(s, a) &= r_{s}^{a} + \gamma \sum_{s^{\prime} \in \mathcal{S}}p(s^{\prime}, r \mid s, a) v_{\pi}(s^{\prime}) \end{aligned} $$

Bellman equation과 관련된 표현형은 뒤에서 정리하도록 한다. 마지막 식을 보면서 MDP에 대한 정보를 알아야만 사용할 수 있음을 볼 수 있다. 보상과 확률전이행렬에 대한 정보를 필요로 하는데 이 정보는 MDP, 즉 환경에 대한 정보로 이를 알 수 있으면 사용할 수 있고 만약 모른다면 MDP에 대한 정보 없이 사용할 수 있는 $\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right]$를 사용하면 된다.

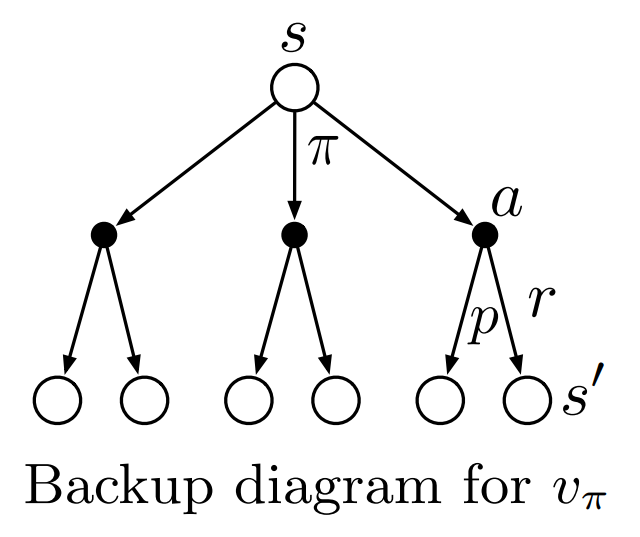
위의 그램은 backup diagram인데 강화학습에서 상태와 $s-a-s^{\prime}$으로의 과정을 이해할 때 도움이 많이 된다. 흰 원은 상태, 검은 원은 state-action pair이다. 여기서 중요한 것은 현재 상태 $s$와 다음 상태 $s^{\prime}$ 사이에는 두 개의 확률과정이 있다는 것이다. 첫 번째는 정책에 의한 확률로 $s$는 정책 $\pi$가 정의하는 확률 $\pi(a \mid s)$에 따라 $a$를 선택한다. 그리고 해당 행동 $a$를 실행하면 그 다음에는 환경이 갖고 있는 확률에 의해 다음 상태인 $s^{\prime}$이 보상과 함께 결정된다. 위의 Bellman euqation은 backup diagram에 보이는 과정들을 확률에 대한 가중평균을 했다고 이해하면 훨씬 이해하기도, 암기하기도 쉽다.

가치함수 $v_{\pi}$는 Bellman equation의 유일한 해이며 이는 이후에 $v_{\pi}$를 계산하고 근사하고 학습하는 과정에서 자세히 다루게 된다.

Bellman Expectation Equation

Bellman Expectation Equation은 강화학습분야에서 전반적으로 사용되는 핵심 개념으로 모두 이해하고 암기하자. 앞서 다룬 내용을 이해하였다면 식을 외우는 것은 그리 어렵지 않다.

3.6 Optimal Policies and Optimal Value Functions

강화학습 문제를 푼다는 것은 주어진 MDP의 최적정책을 찾았다는 것과 같다. 최적정책이란 앞으로의 기대보상을 최대로 하는 정책이며 최적정책은 다른 어떤 정책보다도 높은 expected return을 보장하므로 최적정책을 찾으면 강화학습 문제의 목적을 달성하게 되는 것이다.

이를 식으로 표현하기 위해 정책에 부등식을 사용하게 되는데, 정책 $\pi$가 $\pi^{\prime}$ 모든 상태 $s \in \mathcal{S}$에 대해 $v_{\pi}(s) \geq v_{\pi^{\prime}}(s)$일 때, $\pi \geq \pi^{\prime}$이라고 쓴다. 식에서 말하듯 어느 한 상태에서라도 $\pi{^\prime}$이 $\pi$보다 높은 expected return갖는다면 이와 같이 쓸 수 없다.

여기서 신비로운(?) 정리 하나를 확인하고 가자.

최적정책에서의 상태가치와 행동가치 함수는 다음과 같다.

위의 상태/행동가치는 최적정책에서의 상태와 행동가치이므로 Bellman expectation equation은 최적정책을 반영해 다음과 같이 쓸 수 있게 된다.

최적정책에서의 backup diagram은 다음과 같이 그려진다.

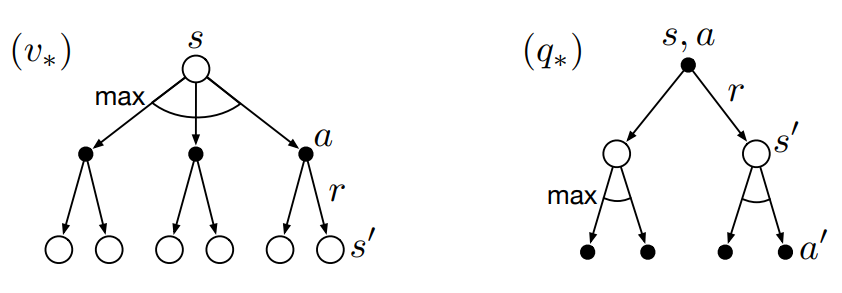
부채꼴 모양의 $\operatorname{max}$연산자는 앞서 보았던 Bellman expectation equation이 기댓값을 계산했던 것과는 달리 최대값을 취함을 의미한다.

앞서 말한바와 같이, finite MDP에 대해서 Bellman optimality equation이 유일한(unique) 해를 가진다는 것이 밝혀져 있다.

그렇다면 상태/행동가치에 대해서 optimal equation을 푸는 것이 최적정책과 어떻게 연결될까? Optimal state/action value function을 구했다면 최적정책은 간단하게 각 상태에서 최대의 return을 주는 상태 또는 행동을 선택하면 된다. 다르게 말하면 optimal state/action value function에 대해서 greedy한 선택을 하면 이 자체가 최적정책이 되는 것이다.

Bellman optimality equation을 풀면 강화학습의 문제를 푸는 것과 같지만 이는 쉽지가 않다. 예를들어 앞서 확인한 상태가치에 대한 Bellman optimality equation을 보자. $$v_{*}(s) = \max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right]$$ 결과적으로 위 식을 풀면 되는 것인데 위 식은 생각보다 많은 조건을 필요로한다. 일단 위의 식을 보면 $p$를 사용하고 있는데 $p$를 안다는 것은 MDP의 dynamics를 알고 있어야 한다는 것이다. 즉, 문제환경이 어떻게 움직일지 알고 있어야 한다는 상당히 강력한 전제조건이 붙게된다. 이와 더불어 수 많은 상태와 행동에 대해 각각 $\sum$, $\max$가 사용되므로 계산량도 상당할 뿐더러, MDP이므로 Markov property를 만족해야 한다. 따라서 현실적으로 Bellman optimality equation을 정확하게 풀기는 어려우며 근사적으로 푸는 방법들이 사용된다. 예로, 교재의 다음단원에서 다루는 dynamic programming도 그 중 하나의 방법이다.

Bellman Optimality Equation

앞에서 Bellman expectation equation과 마찬가지로 Bellman optimality equation도 아래와 같이 요약할 수 있다. Bellman expectation equation과 Bellman optimality equation 모두 이후 강화학습 개념이해에 매우 중요한 내용으로 모두 암기하는 것을 권장한다.

3.7 Optimality and Approximation

앞서 언급한 바와 같이 optimal policy를 찾는데에는 여러 어려움이 따른다. 우선 대부분의 경우 환경이 어떻게 변화할지에 대해 모르는 경우(model-free)가 많다. 환경의 dynamics를 안다고 해도 계산량의 문제는 결코 작은 문제가 아니다. 당장 바둑을 예로 보더라도 바둑은 환경과 규칙을 모두 알고 있는 상황이지만 수 많은 경우의 수가 존재한다. 그렇기에 AlphaGo가 바둑에서 프로기사를 압도한 것이 유의미한 발전으로 여겨지는 것이다. 그마저도 좋은 정책을 학습한 것이지 최적정책으로 수렴했는지를 이야기하기는 어렵다.

교재에서 언급하는 다른 어려움으로 memory를 언급한다. 지금 다루는 tabular case, 즉 표의 각 축에 상태와 행동을, 그리고 값으로는 가치를 사용하는 접근을 사용하려면 수 많은 상태와 각 상태별 행동을 모두 나타낼 수 있는 아주 거대한 표를 만들어야 한다. 그리고 많은 경우 이런 거대한 표를 사용하는 접근은 현실적으로 불가능하다. 따라서 상태와 행동에서 가치를 추정하기 위해 함수를 사용하는 방법을 고려해보아야 한다. 다행스럽게도 neural network의 등장덕분에 아주 복잡한 비선형함수를 만드는 것이 가능해졌고 이러한 접근이 강화학습과 만나 deep reinforcement learning이라는 분야로 발전하는 중이다.

강화학습은 기본적으로 return이 높은 행동을 강화하고 return이 낮은 행동을 억제하는 방식으로 학습을 하게된다. 따라서 마주칠 일이 거의 없는 상태에서의 학습을 덜 하면서 자주 발생하는 상황에서의 판단을 향상시키는 방향으로 학습을 전개할 수 있으며, 이는 일반적인 MDP를 근사적으로 푸는 방법과 대비되는 강화학습의 특징 중 하나이다.

3.8 Summary

이번 문서에서는 강화학습의 구성요소와 MDP에 대해 알아보았다. 강화학습은 학습의 주체인 agent와 agent와 상호작용하는 환경이 있으며 이 상호작용은 time step이라는 단위에서 상호작용을 정의하게 된다. 그리고 이 때, agent가 환경에 가하는 작용을 행동(action)으로, 행동을 판단하는 agent가 인식하는 환경을 상태(agent)로 정의한다. 그리고 환경은 행동이 주어지면 그에 대한 보상(rewards)을 agent에게 행동의 결과인 상태와 함께 제공하게 된다. 이 때, agent입장에서 환경에 대한 정보는 완전히 알 수도, 완전히 모를 수도 있다. 정책(policy)은 상태에서 행동으로의 확률분포이다. Agent는 궁극적으로 expected return을 최대화하는 것을 목적으로 삼는다.

강화학습의 문제를 풀기 위해 MDP의 개념을 도입하게 되는데 다루는 범위를 finite MDP, 즉 상태, 행동, 보상이 유한개인 공간으로 정의해 다루게 된다.

Return은 앞으로 받게 될 보상의 총합이다. 다만, 수학적 편의성과 continuing task에 일관성있게 정용하기 위해 discount라는 개념을 도입해 미래의 보상에 대해 일정비율로 discount하게 된다.

가치함수는 상태가치와 행동가치로 나누어 볼 수 있다. 주어진 정책을 따를 때 특정 상태에서의 expected return을 상태가치라 하며, 특정 상태와 행동의 쌍에 대한 expected return을 행동가치라고 한다. 이 둘은 Bellman expectation equation으로 표현할 수 있다. 최적정책(optimal policy)는 다른 어떤 정책보다도 더 크거나 같은 expected return을 보장하는 정책으로, 이러한 정책에서의 상태가치와 행동가치를 각각 최적상태가치, 최적행동가치라고하며 이는 Bellman optimality equation으로 표현할 수 있다.

Agent가 환경에 대한 dynamics를 모두 알고 있는지(complete knowledge), 일부라도 모르고 있는지(incomplete knowledge)에 따라서 문제에 대한 접근방법이 달라지게 된다. 이 때 dynamics를 알고 있다면 다음 단원에서 다룰 dynamic programming기반의 방법을 적용해 접근할 수 있으며, dynamics를 모른다면 Monte Carlo나 temporal difference와 같은 방식을 사용하게 된다. 환경에 대한 dynamics를 모두 알고 있다고 하더라도 환경이 복잡해서 상태와 행동을 표에 적는 방식으로 나타내는 것이 현실적으로 어렵다면 approximator를 사용해 가치를 추정하는 방식을 사용하게 되면 neural network가 도입된 이후로는 approximator로 neural network를 활용하는 방식이 많이 사용되고 있다.

이처럼 강화학습이 다루는 공간은 복잡한 공간으로 여러가지 제약이 필요하다. 따라서 앞으로 다루게 되는 내용들을 볼 때 이론적으로 최적정책을 구하는 방법과 현실적으로 agent가 최적정책을 근사하는 방법으로 구분해서 보는 것이 좋다.

Reference

• Sutton, R. S., Barto, A. G. (2018). Reinforcement learning: An introduction. Cambridge, MA: The MIT Press.
• Wikipedia: Reinforcement Learning