Chapter 2: Multi-armed Bandits

강화학습 공부를 시작할 때 예제로 Multi-armed bandit 문제가 자주 사용된다. 이 문제는 슬롯머신에서 파생한 것으로, 상대방(여기서는 슬롯머신)이 어떻게 행동하는지에 대한 정보를 모르는 상태에서 최적의 전략을 선택해야 한다는 점에서 좋은 강화학습 예제가 된다.

강화학습을 다른 기계학습방법과 구분지어주는 가장 큰 특징은 학습하는 과정에 있다. 강화학습은 기계학습처럼 정답을 알려주면서 학습하는 것이 아니라 각 행동을 스스로 평가하면서 학습한다. 즉, 학습을 하기위한 feedback의 종류가 다르며 교재에서는 선택한 행동을 기반으로 하는 feedback을 evaluative feedback, 그리고 선택한 행동과 상관없이 주어지는 feedback을 instructive feedback으로 설명한다.

Evaluative feedback은 행동이 얼마나 좋았는지에 대한 추정일 뿐, 최선의 행동이었는지를 의미하지는 않는다. 미로찾기에서 agent는 특정 상태에서 “오른쪽으로 가는 선택을 할 경우, 기대되는 보상은 1.3정도입니다"와 같은 feedback을 받는다고 생각하면 된다. 대조적으로, instructive feedback은 지도학습의 target label로 생각하면 이해가 편하다. Agent에게 “이 행동이 정답이다!“라고 명시적으로 알려주는 것이다. 이미지 분류문제에서 특정 이미지가 자동차면 자동차고 의자면 의자이지 target label을 “꽤나 자동차 사진인것 같군요!“라고 하지 않는 것으로 생각하면 된다.

Chapter 2에서 다루는 multi-armed bandit문제는 한 가지 상황에서 어떻게 행동해야 하는지만을 다루는 문제로 evaluative feedback을 이해할 수 있는 토대를 제공하며 나아가 instructive feedback과 어떻게 조합할 수 있는지를 알게 해준다. 슬롯머신과 같은 One-armed bandit상황에 비유하면 슬롯머신을 하는 사람을 레버를 당기는게 가능한 유일한 행동이며 그 결과 얻을 수 있는 상황은 슬롯머신의 결과(state)와 이에 따른 보상일 뿐이므로 한 가지 상황이라 볼 수 있다.

이번 챕터에서는 non-associative setting에서의 evaluative aspect를 다룬다. Non-associative setting은 어떤 setting을 말하는지를 먼저 간단히 알아보자.

• Non-associative:

  • 상황에 대해 독립적이다. 즉 각각의 상황은 독립사건으로 생각할 수 있다.
  • 다른 상황에서의 행동 연관지을 필요가 없다.
  • Stationary한 문제라면 최선의 행동이 존재하며 이를 선택하면 된다. Non-stationary하다면 최선의 행동을 추적하면서 선택하면 된다.
  • 예) 슬롯머신에서 지금 레버를 당기는 것과 이전에 레버를 당기는 상황은 동일하다. 슬롯머신이 고정된 확률에 의해 결과를 보여준다면 이는 Stationary & non-associative한 상황이다.

• Associative:

  • 상황에 의존적이다.
  • 해당 상황에서 행동으로의 함수(정책)를 통해 최적의 행동을 결정한다.
  • 예) 게임의 진행을 생각해보면 내가 현재 보고있는 상황은 이전에 선택한 행동의 결과이다.

그러면 본격적으로 multi-armed bandit problem을 살펴보자.

2.1 A k-armed Bandit Problem

당신은 슬롯머신앞에 앉아있다. 그런데 일반적인 슬롯머신과 달리 이 슬롯머신은 $k$개의 레버를 가지고 있다. 당신이 레버를 당길때마다 슬롯머신은 점수를 보여줄 것이고 점수는 각각의 레버가 갖고 있는 고유의 고정된 확률분포(stationary probability distribution)에 의해 결정된다. 당신의 목표는 점수의 총합을 최대한 크게 만드는 것이며 당신은 레버를 1000번 당겨볼 수 있다. 이 때 당신은 어떤 전략을 선택할 것인가?

이 상황이 바로 $k$-armed bandit problem문제가 다루는 상황이다. 가장 높은 점수를 주는 레버가 무엇인지 알면 주구장창 그 레버만 당겨버리면 되겠지만 우리는 각 레버의 확률분포에 대한 사전지식이 없다.

그렇다면 레버마다 가지고 있는 확률분포에 대해 우리가 필요한 정보는 무엇일까? 바로 그 레버를 선택했을 때 점수에 대한 기댓값이다.

$$ q_{*}(a) \doteq \mathbb{E}[R_t \vert A_t = a] $$

즉, 레버마다 time step $t$에서 행동 $a$를 선택했을 때의 점수에 대한 기댓값을 알 수 있다면 그 다음 선택은 그 레버만 신나게 당기면 되는 것이다. 우리는 정확한 값은 알 수 없고 추정만 할 수 있으므로 time step $t$에서 추정한 행동 $a$에 대한 가치를 $Q_t(a)$라고 하며 이 값을 실제 가치인 $q_{*}(a)$와 최대한 가깝게 추정해내는 것이 목표가 되는 것이다.

그렇다면 학습 중의 상황을 생각하자. 행동가치를 추정하는 과정에서 그 값이 얼마나 정확한지를 떠나서 time step $t$에서 가장 큰 가치를 갖는 행동이 존재하게 된다. 이러한 행동을 greedy action이라 한다. 해당 시점에서 가장 큰 가치를 갖는 행동을 선택하는 것을 현재 알고있는 행동가치에 대한 지식을 exploiting한다고 한다. Nongreedy action을 선택하는 것은 exploring한다고 한다. 이미 확률분포에 대한 확신이 있다면 exploiting하는 것이 효율적이지만 불확실성이 크고 앞으로 많은 시도를 해볼 수 있다면 exploring을 통해 더 좋은 결과를 얻을 가능성을 탐색하는 것이 좋을 것이다. Exploring하는 동안 단기적으로는 보상이 적을 수 있지만 더 나은 행동을 찾게 된다면 새로운 행동을 exploit하면서 장기적으로 더 큰 보상을 기대할 수 있다. Exploitation과 exploration을 동시에 할 수는 없으므로 이 둘의 균형을 조절하는 것은 그 자체로 강화학습에서 중요한 문제이다.

교재에서는 기초적인 방식의 Balancing methods를 사용해 항상 exploitation을 사용하는 것 보다 balancing method를 쓰는게 더 좋은 결과를 보여준다는 것을 보여주며 복잡한 형태의 balancing method는 따로 다루지 않는다.

2.2 Action-value Methods

행동가치를 추정하는 다양한 방식이 있다. 이러한 방식을 통틀어 action-value methods 라고 부른다. 행동가치란 해당 행동을 선택하였을 때 보상의 기댓값임을 상기하자.

그렇다면 행동가치는 어떻게 계산하는지에 대해 살펴보자. 다음은 sample-average method라는 방식으로 행동가치를 평균으로 간단하게 구하는 방법이다. 행동을 통해 얻은 보상을 해당 행동을 시행한 횟수로 나누면 나누면 얻을 수 있다.

행동가치를 추정하는 가장 간단한 방법으로 행동을 취했을 때 얻은 결과에 단순 평균을 취하는 방법을 생각해 볼 수 있다. 이러한 방식을 Sample-average Method 라고 한다. $$\begin{aligned}Q_t(a) &\doteq \frac{\text{sum of rewards when } a \text{ taken prior to }t}{\text{number of times } a \text{ taken prior to }t} \ &= \frac{\sum_{i=1}^{t-1} R_i \cdot \mathbb{1}_{A_i=a}}{\sum_{i=1}^{t-1} \mathbb{1}_{A_i=a}} \end{aligned}$$ 위 식에서 $\mathbb{1}_{\text{predicate}}$은 predicate이 True일 때 1, 아닐 때 0인 random variable이다. 만약 분모가 0이라면 사전에 정의된 default값을 value로 반환하며 분모가 무한히 커지면, 즉 time step $t$에서의 행동이 무한히 커지면 큰 수의 법칙(The law of large numbers)에 의해 $Q_t(a)$는 $q_{*}(a)$로 수렴한다.

행동가치에 대해 greedy한 선택은 다음과 같이 표현할 수 있다.

$$ A_t = \argmax_{a}Q_{t}(a) $$

단순하게 행동가치가 가장 큰 행동 $a$를 선택하는 것이다. 하지만 앞서 언급되었듯, greedy한 방식만 사용하게 되면 더 나은 행동을 찾을 수 있는 기회를 갖지 못한다. 따라서 간단한 대안으로 사용할 수 있는 방식은 일정 확률 $\varepsilon$에 대해 추정한 행동가치와 상관없이 선택 가능한 행동들 중에서 임의로 행동을 선택하는 것이다. 이 방식의 장점은 단순하면서도 시행이 많아지게 되면 모든 행동들이 sampling되면서 $Q_t(a)$가 $q_{*}(a)$로 수렴하게 된다는 것이다. 이러한 방식을 $\boldsymbol{\varepsilon}$-greedy 방법이라고 부른다.

2.3 The 10-armed Testbed

$\varepsilon$-greedy 방법이 greedy방법에 비해 정말 효과가 있는지를 알아보기 위해 다음과 같은 실험을 살펴보자.

2,000번 랜덤시행을 한 10-armed bandit이 있다고 해보자. 각기 다른 값이 설정된 슬롯머신 10대가 있는 것이다. 그리고 행동 각각 $a = 1, \ldots, 10$이라 하고 $q_{*}(a)$는 평균 0, 분산이 1인 정규분포로 선택된 값이다. $q_{*}$는 실제 행동가치로 agent는 알 수 없는 값임에 유의한다. agent는 회색밴드로 표현된 분포에 따라 보상을 받게 되며 이 값이 agent가 관측할 수 있는 보상이다. 이러한 테스트 상황을 10-armed testbed라고 부른다.

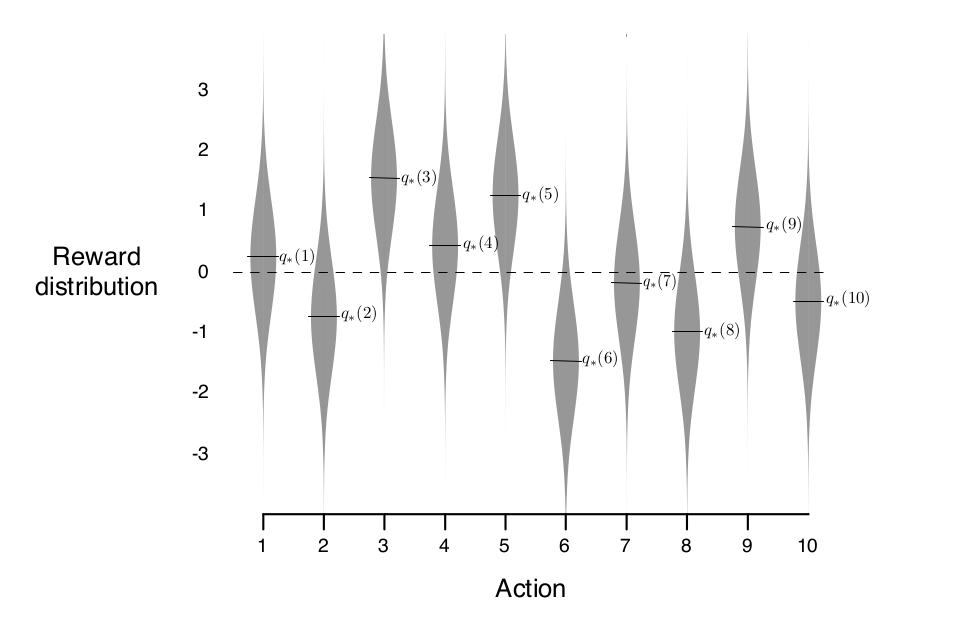
이 문제에 대해 sample-average method의 $\varepsilon$을 0, 0.01, 0.1로 다르게 적용해 각각 2000번 시행한 평균은 다음과 같다.

먼저 greedy한 전략을 썼을 떄의 평균 보상을 보면 1에 도착하고 증가하지 않는다. 행동 3의 기댓값이 1.55로 행동 3을 선택하는 최고의 전략에 비할 때 greedy한 agent는 suboptimal에 최적화 되었음을 알 수 있다. 아래의 optimal action비율(여기서는 행동 3을 선택한 경우)를 보더라도 greedy agent는 33%정도에 머무르고 있다. 대조적으로 $\varepsilon$-greedy agent는 모두 점진적으로 평균 보상과 optimal action비율이 향상되는 것을 볼 수 있다. (물론 무한정 좋아지지는 않는다. 0.1로 설정된 경우 91% 확률로 optimal action을 선택한다) 충분히 exploration이 일어났다면 $\varepsilon$을 점차 줄여 더 높은 return을 기대할 수도 있다.

$\varepsilon$-greedy의 선택은 testbed의 노이즈에 따라 다르게 선택될 수 있다. 지금은 testbed가 평균 0, 분산이 1이었지만, 분산이 10이었다면 더 많은 exploration이 필요했을 것이고 $\varepsilon$-greedy와 greedy의 차이는 더 커졌을 것이다. 하지만 분산이 0이었다면 greedy는 시행 즉시 $q_{*}$를 알 수있게 될 것이므로 $\varepsilon$-greedy가 필요없는 상황이 된다. 하지만 이런 deterministic한 상황이라 하더라도 $q_{*}$가 조금씩 변하는 non-stationary한 상황이라면 nongreedy action이 기존의 greedy action보다 높은 return을 제공할 가능성이 있으므로 exploration이 필요하다.

2.4 Incremental implementation

단순하지만 행동가치를 추정하는 방법인 sample-average method를 보았다. 이번에는 제한된 자원만 있는 상황에서 어떻게 sample-average method를 적용할 수 있는지, 그리고 실제 행동가치가 고정된채로 유지되는 것이 아니라 변화하는 환경에서는 어떻게 대응할지에 대해 알아보자.

Incremental implemenation에서 다루는 내용은 간단하게 말하면 이동평균으로 평균을 구하는 방식이다. 어떤 armed bandit의 행동가치를 다음과 같이 정의해보자.

$$ Q_{n} \doteq \frac{R_{1} + R_{2} + \cdots + R_{n-1}}{n - 1} $$

위 식은 $n-1$ time step까지의 보상 평균에 해당하는 값으로 보상을 모두 들고다닐 필요 없이 평균값 하나만 저장하면 되어 많은 메모리공간을 차지하지 않는다. 아래 유도는 이전까지의 행동가치와 현재 보상, 이 두 정보만 알면 행동가치를 update할 수 있음을 보인다.

$$ \begin{aligned} Q_{n+1} &= \frac{1}{n} \sum_{i=1}^{n} R_{i} \cr &= \frac{1}{n} \left( R_{n} + \sum_{i=1}^{n-1} R_{i} \right) \cr &= \frac{1}{n} \left( R_{n} + (n-1) \frac{1}{n-1} \sum_{i=1}^{n-1} R_{i} \right) \cr &= \frac{1}{n} \left( R_{n} + (n-1) Q_{n} \right) \cr &= \frac{1}{n} \left( R_{n} + n Q_{n} - Q_{n} \right) \cr &= Q_{n} + \frac{1}{n} \left[ R_{n} - Q_{n} \right] \end{aligned} $$

행동가치를 위와 같이 update 할 수 있다는 것은 간단하게 확인이 되지만 더 중요한 것은 위와 같은 update의 형태이다. 이 책 전반에 걸쳐서 다음과 같은 update 방식은 매우 자주 등장한다.

$$ \operatorname{NewEstimate} \leftarrow \operatorname{OldEstimate} + \operatorname{StepSize} \left[ \operatorname{Target} - \operatorname{OldEstimate} \right] $$

여기서 $ \left[ \operatorname{Target} - \operatorname{OldEstimate} \right] $부분을 추정에 대한 error라고 한다. 또한 $\operatorname{StepSize}$는 time step이 증가할수록 점점 작아지는 변화하는 값임에 유의하자.($n$번째 행동에 대한 보상은 $\operatorname{StepSize}$가 $\frac{1}{n}$만큼 적용된다) 이후 책에서는 $ \operatorname{StepSize} $를 $\alpha$, 또는 $\alpha_{t}(a)$로 표기한다.

Simple Bandit Algorithm

Sample average method와 $\varepsilon$-greedy을 사용해 armed-bandit의 행동가치를 추정하는 bandit 알고리즘의 pseudocode는 다음과 같다.

우선 모든 행동 대해 행동가치와 시행횟수는 0으로 초기화가 된다. 그리고 시행이 발생할때 마다 loop을 돌면서 값을 update 하는 구조이다. $\varepsilon$-greedy이므로 $1-\varepsilon$의 확률로 행동가치가 가장 큰 행동을 선택하고 $\varepsilon$의 확률로 무작위 행동을 선택한다. 선택한 행동으로 bandit의 레버를 당기면 보상이 주어지고 해당 게임은 끝나게 된다. (후에 다루겠지만 이러한 성질로 인해 bandit은 1-step MDP로 볼 수 있다) 시행을 했으니 counter 역할을 하는 $N(A)$를 1 올려주고 위의 식을 이용해 행동가치를 update해주면 된다.

2.5 Tracking a Nonstationary Problem

지금까지 다룬 bandit 문제는 초기 분포가 주어지고 그 분포가 변하지 않는다고 가정하였다. 하지만 조금더 영악한 bandit일 때를 생각해보자. 만약 특정 bandit의 return 기댓값이 높다는 것이 알려지면 사람들은 주구장창 해당 bandit의 레버만 당겨버릴 것이다. 만약 bandit이 스스로의 분포를 조금씩 바꾸어간다면 어떻게 될까? 문제가 더 dynamic해지게 된다. 지금의 최선책이 이후에도 최선책임을 보장할 수 없게 되는 것이다. 그리고 실제 문제들은 고정된 확률분포(stationary)보다는 바뀌는(nonstationary) 경우가 더 많다. 문제가 바뀌었으므로 전략도 바뀌어야 한다. 이에 대응하는 방법으로 최근 보상에 더 집중하는, 즉 가중치를 더 주는 방법을 생각해볼 수 있다. 아무래도 최근 값이 행동가치 더 많은 영향을 준다면 nonstationary한 실제 행동가치를 추종(tracking)할 수 있을 것이라는게 기본적인 아이디어다. 위의 공식에서 가중치에 해당하는 부분은 step-size parameter였다. 앞에서는 모든 step에 대해 동일한 가중치를 주었다면 이번에는 최근 가중치를 더 크게 주도록 설정하면 된다. Step-size parameter를 $\alpha$라고 하고 위의 식을 전개하면 다음과 같이 정리할 수 있다.

$$ \begin{aligned} Q_{n+1} &\doteq Q_{n} + \alpha[R_{n} - Q_{n}] \cr &= \alpha R_{n} + (1-\alpha) Q_{n} \cr &= \alpha R_{n} + (1-\alpha) [\alpha R_{n-1} + (1-\alpha) Q_{n-1}] \cr &= \alpha R_{n} + (1-\alpha)\alpha R_{n-1} + (1-\alpha)^{2} Q_{n-1} \cr &= \alpha R_{n} + (1-\alpha)\alpha R_{n-1} + (1-\alpha)^{2} \alpha R_{n-2} + \cr &\quad \cdots +(1-\alpha)^{n-1} \alpha R_{1} + (1-\alpha)^{n} Q_{1} \cr &= (1-\alpha)^{n} Q_{1} + \sum_{i=1}^{n} \alpha (1-\alpha)^{n-i} R_{i} \end{aligned} $$

$\alpha \in (0, 1]$이며 첫번째 줄을 보면 $\alpha$라는 가중치가 현재 보상에 적용되고 나머지 $1-\alpha$는 최근 행동가치의 가중치로 들어간 것을 볼 수 있다. 이후 전개식은 식을 바꾸어 쓴 것일 뿐이므로 가중치의 합은 1로 보존된다. 즉, $ (1-\alpha)^{n} + \sum_{i=1}^{n} \alpha(1-\alpha)^{n-i} = 1 $이다. 주목할 부분은 현재의 보상 $R_{i}$의 가중치인 $ \alpha(1-\alpha)^{n-i} $인데, 가장 최근인 $R_{n}$의 가중치는 $\alpha$이다. 반면 최초의 보상 $R_{1}$의 계수는 $\alpha (1 - \alpha)^{n-1}$이다. 시행 $i$가 커질수록 $ (1-\alpha) < 1$이므로 더 큰 가중치를 받게 된다. 매 time step이 커질수록 $1/(1-\alpha) $배만큼 큰 가중치를 받으므로 이를 exponential recency-weighted average라고도 한다.

이 때, 아무 step-size parameter나 사용한다고 해서 행동가치가 수렴하지는 않는다. 수렴성을 보장하기 위해서 step-size parameter는 다음 두 조건을 만족해야 한다.

$$ \begin{aligned} \sum_{n=1}^{\infty} \alpha_{n}(a) &= \infty \cr \sum_{n=1}^{\infty} \alpha_{n}^{2}(a) &< \infty \end{aligned} $$

첫번째 식은 initial condition과 random fluctuation을 넘어서기 위해서 step-size parameter는 충분히 커야한다는 의미이고 두번째 식은 수렴을 보장해야 하므로 충분히 작아야 한다는 것이다. Sample-average method에서 사용한 step-size parameter는 $\alpha_{n}(a) = \frac{1}{n}$이었는데 이는 위의 두 식을 만족한다.

$$ \begin{aligned} \sum_{n=1}^{\infty} \frac{1}{n} &= \infty \cr \sum_{n=1}^{\infty} \frac{1}{n^{2}} &= \frac{\pi^{2}}{6} < \infty \end{aligned} $$

하지만 실무적으로는 위의 두 조건을 만족한다고 해도 수렴하는 속도가 너무 느리거나 수렴속도를 맞추기 위해서 상당한 tuning을 거쳐야 한다는 문제가 있다. 따라서 step-size parameter의 수렴조건은 이론적인 의의는 있지만 application이나 실험적 연구에서는 거의 사용되지 않는다.

2.6 Optimistic Initial Values

학습을 더 잘 시키기위한 기법 중 하나인 optimistic initial value에 대해서 알아보자.

지금까지 다룬 행동가치기반의 접근방법뿐만 아니라 앞으로 다룰 방법들 중 대부분은 어떠한 형태로든 초기값을 설정해주어야 한다. 사전지식(prior)이 없는 상황이라면 uniform하게 설정하거나 단순하게 난수로 생성하는 경우가 많다. 물론 사전지식이 있다면 이를 반영해 초기값을 설정할 수도 있다. 학습과정의 시작점은 이 초기값에 의해 정해지는 만큼 초기값을 기준으로 하는 iterative algorithm들은 초기값에 bias될 수 밖에 없다.

Optimistic inital value는 exploration을 장려하는 방향으로 초기값을 설정하는 기법이다. 아이디어는 매우 간단하다. 모든 행동에 대한 행동가치를 양의 특정 값으로 설정하는 것이다. 이렇게되면 agent입장에서는 초반에 모든 행동들이 가치있는 행동으로 보이게 된다. 학습과정에서 특정한 행동의 결과가 좋지 않았다면 여기서 오는 실망은 해당 행동의 행동가치를 감소시키게 될 것이다. 초기값이 모두 양수로 설정되었으므로 agent는 방금 시도한 행동을 제외한 나머지 행동을 더 가치있다고 생각하며 optimistic inital value는 이를 이용해 exploration을 촉진시킬 수 있다.

위의 그림은 optimistic initial value와 $\varepsilon$-greedy를 10-armed bandit에 적용했을 때의 결과이다. Optimistic inital value를 적용한 setting에서는 모든 행동에 대한 행동가치를 5로 부여하였다. Agent는 모르는 정보지만, 실제 행동가치는 $q_{*}(a)$가 $\mathcal{N}(0, 1)$에서 추출된 것임을 감안하면 매우 optimistic한 값으로 초기값을 설정했음을 알 수 있다. 그리고 이러한 설정으로 인해 agent는 baseline보다 훨씬 더 exploration을 적극적으로 하게 된다. Initial value $Q_1(a) = 5$로 시작하지만 학습이 진행됨에 따라 행동의 추정가치는 감소하기 시작할 것이고 초반부에 다양한 행동을 시도할 것임을 짐작할 수 있다. 대조군인 baeline은 $\varepsilon$-greedy를 사용하고 initial value가 $Q_1(a) = 0$으로 설정되었다.

초반부를 살펴보면 optimistic initial value의 특징이 두드러지는데, 더 많은 탐색을 하게 되므로 optimial action 선택비율이 $\varepsilon$-greedy에 비해 훨씬 낮다. 하지만 시간이 지나면서 optimal action을 baseline인 $\varepsilon$-greedy 보다 더 빠르게 찾아 optimal action의 선택비율이 급격하게 높아지는 것을 볼 수 있다. 방법이 아주 간단한 점을 감안할 때, 유의한 이점이라고 볼 수 있다.

하지만 이러한 optimistic initial value를 범용적으로 사용할 수 있는 것은 아니다. 당장 nonstationary 문제들에는 적용하기가 어렵다. 초반부 exploration을 장려하는 효과는 있지만 문제가 nonstationary라면 확률분포가 바뀌게되어 초반의 exploration 결과를 계속 사용할 수 없으므로 효율적이지 않다. 이처럼 초기값에 사용하는 trick들은 대게 nonstationary문제에 적용하기 어렵다는 단점이 있다.

2.7 Upper-Confidence-Bound Action Selection

Optimistic initial value가 초기값에 대한 trick이었다면 Upper-Confidence-Bound(UCB)는 행동선택에 대한 trick이다. $\varepsilon$-greedy는 non-greedy한 방식으로 새로운 행동을 시도하며 exploration을 해볼 수 있는 간단하지만 강력한 방법이다. 하지만 UCB는 $\varepsilon$-greedy가 $\varepsilon$의 확률로 무작위로 action을 고른다는 것에 주목한다. Q-value, 즉 행동가치 중에는 이미 여러번 해당 행동을 시도해서 거의 수렴한 Q-value도 있을 것이고, 정말 시도를 아예 해보지 않아 Q값을 제대로 추정하지 앟은 Q-value도 있을 것이다.

UCB는 Exploration을 할 때, “무작위로 행동을 고르지 말고, 지금까지 선택이 덜 되어 더 불확실한 행동가치를 갖는 행동을 선택하도록 유도할 수는 없을까?”

UCB는 이러한 문제의식을 반영한 방법이다. UCB에서 non-greedy action은 다음의 식에 따라 선택한다.

$$ A_{t} \doteq \argmax_{a} \left[ Q_{t}(a) + c \sqrt{\frac{\ln t}{N_{t}(a)}} \right] $$

$\argmax_{a} Q_{t}(a)$로만 고른다면 greedy방법이다. 하지만 뒤의 항이 UCB의 특징을 설명해준다. 우선 분자의 log를 보면, log는 증가함수이므로 time step $t$가 증가할수록 선택할 가능성이 커진다고 볼 수 있다. 반면 $N_{t}(a)$는 해당 time step이전까지 행동 a가 선택된 횟수를 의미한다. 더 많이 선택될수록 분모가 커지면서 Q-value 추정에 대한 불확실성이 적어진다는 것을 반영해준다. 이 둘의 조합인 $\sqrt{\frac{\ln t}{N_{t}(a)}}$가 UCB의 불확실성을 표현하게 된다. 행동 a가 선택되면 $N_{t}(a)$가 증가하면서 해당 행동의 불확실성은 감소하게 된다. 반면, 분자인 $\ln t$는 행동 a의 선택여부와 상관없이 증가하게 된다. log값이므로 증가폭은 점점 감소하지만 여전히 상한(upper bound)이 정해지지는 않는다. 따라서 분자항은 불확실성을 계속 증가시키며 선택되지 않은 행동이 선택될 가능성을 크게 만들어주고 분모항에서는 실제 행동 a가 발생했을 경우에 커지게되면서 불확실성을 낮추어주게 된다. 예로, 꽤 많은 time step이 지났는데 한번도 실행되지 않은 action의 경우 $ \underset{a}{\operatorname{argmax}} \left[ Q_{t}(a) + c \sqrt{\frac{\ln t}{N_{t}(a)}} \right] $에 의해 선택될 가능성이 상대적으로 커지게 될 것이다. $c$는 양수로 exploration의 정도를 결정하게 된다. $c$값이 크다면 행동선택에 있어서 불확실성의 가중치가 더 커지게 될 것이다.

Optimistic initial value와 마찬가지로 UCB를 적용한 것과 $\varepsilon$-greedy의 결과를 10-armed bandit에서 비교하면 다음과 같다.

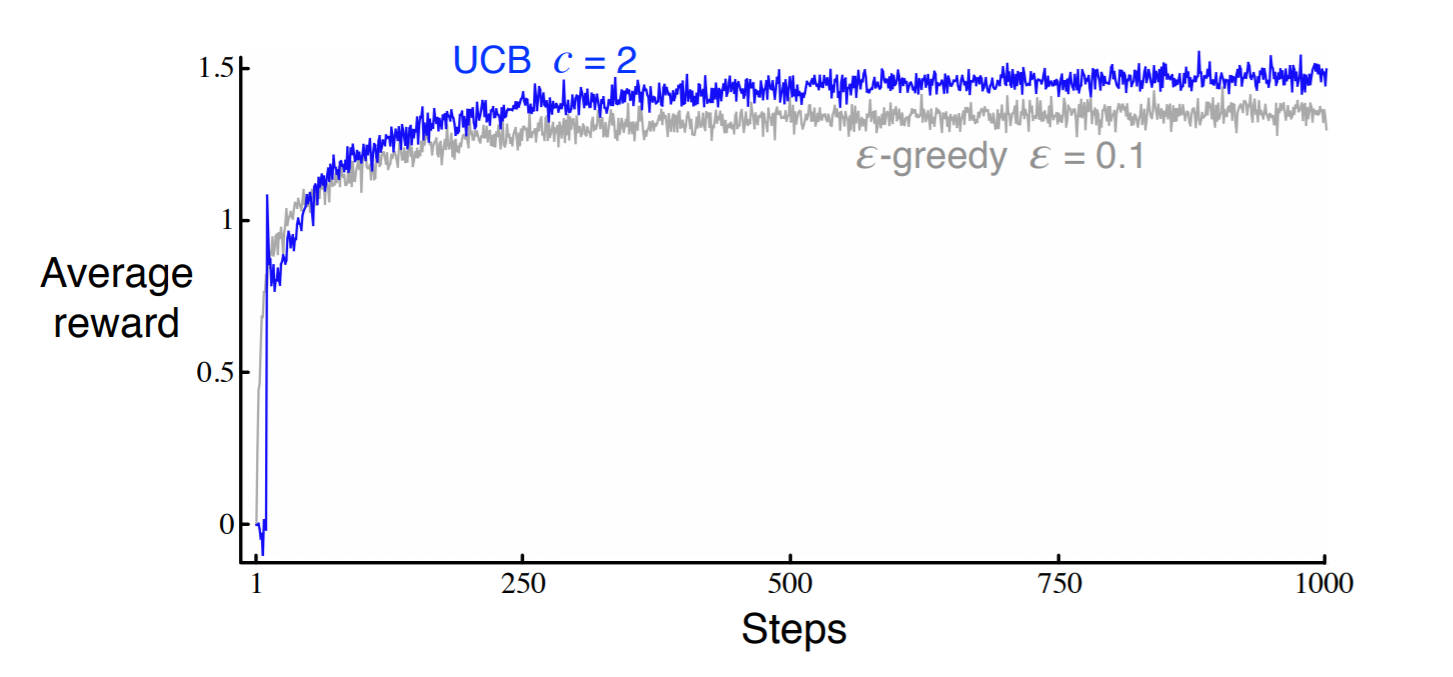
UCB는 전반적으로 잘 작동하지만 bandit문제와 같이 단순한 문제를 벗어나면 적용하기가 어렵다는 단점이 존재한다. UCB 역시도 nonstationary 문제에 취약하며 상태공간이 큰 경우에도 적용하기가 어렵다. $N_{t}(a)$를 충분히 확보해야 불확실성을 잘 추정할 수 있는데, 상태공간이 매우 크다면 각 상태에서 특정 행동을 하는 횟수 자체가 매우 적어질 것이기 때문이다. 특히, 이렇게 상태공간이 큰 상황에서는 function approximator를 사용해 상태공간에 대해 근사를 하게 되는데 이러한 function approximation을 하게 될 경우 불확실성을 반영하기가 어려워져 UCB 사용에 어려움이 생긴다.

2.8 Gradient Bandit Algorithms

Sample-average method에서는 행동가치를 추정해서 행동에 대한 가치를 부여하였다. 하지만 좌우로 가는 두 가지 행동에서 선택해야하는 상황일 때, 왼쪽과 오른쪽의 행동가치가 10, 100이든 1, 10이든 greedy하게 결정한다면 행동가치의 절대적인 크기는 중요하지 않다. “그렇다면 행동을 결정할 때 상대적인 크기 비교로 접근해보는건 어떨까?“라는 관점이 여기서 다룰 gradient bandit algorithm의 핵심이다.

Gradient bandit algorithm에서는 절대적인 행동가치가 아닌 행동에 대한 preference에 중점을 둔다. Time step $t$에서 action $a$에 대한 numerical preference를 $H_{t}(a) \in \mathbb{R}$라고 할 때, preference가 큰 $H_{t}(a)$를 더 자주 고르게 될 것이다. 행동가치는 현재 상태에서 받을 것으로 기대되는 return의 기댓값이었다. 하지만 preference는 보상의 관점으로 해석되지는 않는다. 물론, 궁극적으로는 더 높은 return을 제공하는 행동에 대해 더 높은 preference를 가져야하겠지만 preference가 가리키는 값이 return을 직접적으로 의미하지는 않는다는 차이가 있다. 이렇게 각 행동에 대한 preference인 $H_{t}(a)$가 있을 때, 이를 확률 다루기위해 soft-max distribution을 사용한다.

$$ \text{Pr} \lbrace A_{t} = a } \doteq \frac{\exp^{H_{t} (a)}}{\sum_{b=1}^{k} \exp^{H_{t}(b)}} \doteq \pi_{t} (a) $$

여기서 $\pi_{t} (a)$는 time step $t$에서 action $a$를 선택할 확률을 말한다. 이외에는 앞에서 다룬 방식과 비슷하다. 초기값으로는 특정 action에 대해 preference를 갖지 않도록 0과 같은 값으로 할당해준다. 이후에는 stochastic gradient descent를 활용해 학습을 시키면 된다.

The Bandit Gradient Algorithm as Stochastic Gradient Ascent

Preference도 결국에는 더 높은 reward의 기댓값을 갖도록 업데이트해야한다. $\left( \mathbb{E}[R_{t}] = \sum_{x} \pi_{t}(x) q_{*}(x) \right)$

$$ H_{t+1} (a) \doteq H_{t} (a) + \alpha \frac{\partial \mathbb{E}[R_{t}]}{\partial H_{t} (a)} $$

물론 실제 행동가치인 $q_{*}$를 알 수는 없으므로 정확한 gradient를 구할 수는 없다. 하지만 이후에 나올 업데이트 방법의 기댓값은 위 식의 업데이트와 같음이 보장된다. 모든 가능한 sample에 대해 업데이트를하면 정확하게 일치할 것이고 stochastic하게 접근하더라도 많은 minibatch들에 대해 적용하면 위의 ideal update에 근사시킬 수 있다.

이제 위의 식을 바탕으로 실제 알고리즘에서 사용할 업데이트 식을 유도해보자.

$$ \begin{aligned} \frac{\partial \mathbb{E}[R_{t}]}{\partial H_{t} (a)} &= \frac{\partial}{\partial H_{t} (a)} \left[ \sum_{x} \pi_{t} (x) q_{*}(x) \right] \cr &= \sum_{x} q_{*}(x) \frac{\partial \pi_{t} (x)}{\partial H_{t} (a)} \cr &= \sum_{x} \left( q_{*}(x) - B_{t} \right) \frac{\partial \pi_{t}(x)}{\partial H_{t} (a)} \end{aligned} $$

$B_{t}$는 baseline으로 $x$와 무관하게 구성된다. 여기서 임의로 $b_{t}$를 추가해도 상관이 없는 이유는 $ \sum_{x} \frac{\partial \pi_{t}(x)}{\partial H_{t} (a)} = 0 $이기 때문이다. $H_{t} (a)$에 의한 확률 $\pi$의 변화량은 각기 다를 수 있으나 확률이므로 이 모두를 더한 값은 0이되어야 하기 때문이다.

그 다음에 사용하는 계산 trick은 $ \pi_{t}(x) $를 분모분자에 곱해주는 것이다. 이렇게 하는 것은 $ \mathbb{E}[R_{t}] = \sum_{x} \pi_{t}(x) q_{*}(x) $형태로 바꾸어주기 위함이다.

$$ \begin{aligned} \frac{\partial \mathbb{E}\left[R_{t}\right]}{\partial H_{t}(a)} &= \sum_{x} \pi_{t}(x)\left(q_{*}(x)-B_{t}\right) \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)} / \pi_{t}(x) \cr &= \mathbb{E} \left[ \left( q_{*} \left( A_{t} \right) -B_{t} \right) \frac{\partial \pi_{t} \left( A_{t} \right) }{\partial H_{t}(a)} / \pi_{t} \left( A_{t} \right) \right] \cr &= \mathbb{E} \left[ \left( R_{t}-\bar{R}_{t} \right) \frac{\partial \pi_{t} \left( A_{t} \right) }{\partial H_{t}(a)} / \pi_{t} \left( A_{t} \right) \right] \end{aligned} $$

여기서 baseline $B_{t}$는 time step $t$에서의 평균보상 $\bar{R}$로 설정되었다. 그리고 $\mathbb{E} \left[ R_{t} \mid A_{t} \right] = q_{*}(A_{t})$이므로 $A_{t}$의 이상적인 행동가치는 해당 행동에 대한 보상의 기댓값이라는 점에서 위와 같이 쓸 수 있다.

이제 편미분항을 정리해보자. Quotient rule을 사용해 편미분항은 아래와 같이 바꾸어 쓸 수 있다.

$$ \begin{aligned} \frac{\partial \pi_{t}(x)}{\partial H_{t}(a)} &=\frac{\partial}{\partial H_{t}(a)} \pi_{t}(x) \cr &=\frac{\partial}{\partial H_{t}(a)} \left[ \frac{e^{H_{t} (x)}}{\sum_{y=1}^{k} e^{H_{t} (y)}} \right] \cr &=\frac{\frac{\partial e^{H_{t} (x)}}{\partial H_{t}(a)} \sum_{y=1}^{k} e^{H_{t} (y)}-e^{H_{t} (x)} \frac{\partial \sum_{y=1}^{k} e^{H_{t} (y)}}{\partial H_{t}(a)}}{ \left(\sum_{y=1}^{k} e^{H_{t} (y)} \right)^{2}} \cr &=\frac{\mathbb{1}_{a=x} e^{H_{t} (x)} \sum_{y=1}^{k} e^{H_{t} (y)}-e^{H_{t} (x)} e^{H_{t}(a)}}{ \left(\sum_{y=1}^{k} e^{H_{t} (y)} \right)^{2}} \cr &=\frac{\mathbb{1}_{a=x} e^{H_{t} (x)}}{\sum_{y=1}^{k} e^{H_{t} (y)}}-\frac{e^{H_{t} (x)} e^{H_{t}(a)}}{ \left(\sum_{y=1}^{k} e^{H_{t} (y)} \right)^{2}} \cr &=\mathbb{1}_{a=x} \pi_{t} (x)-\pi_{t} (x) \pi_{t}(a) \cr &=\pi_{t} (x) \left(\mathbb{1}_{a=x}-\pi_{t}(a) \right) \end{aligned} $$

이 결과를 다시 대입해주면,

$$ \begin{aligned} \frac{\partial \mathbb{E} [R_{t}]}{\partial H_{t}(a)} &= \mathbb{E} \left[ \left( R_{t} - \bar{R}_{t} \right) \pi_{t} \left( A_{t} \right) \left( \mathbb{1}_{a=A_{t}} - \pi_{t} (a) \right) / \pi_{t} \left( A_{t} \right) \right] \cr &= \mathbb{E}\left[\left(R_{t}-\bar{R}_{t}\right)\left(\mathbb{1}_{a=A_{t}}-\pi_{t} (a)\right)\right] \end{aligned} $$

강화학습에서는 식을 기댓값을 사용하는 형태로 나타내려고 노력하는 경우가 많다. 이는 해당 방법을 현실의 문제에 적용하기 위해서 매우 중요한 접근이다. 이유는 기댓값으로 표현이 되었다면 매 time step마다의 정보를 통해 incremental하게 접근할 수 있기 때문이다.

위 식을 한 줄로 표현한다면 다음과 같다.

$$ \begin{aligned} &H_{t+1}(a)=H_{t}(a)+\alpha\left(R_{t}-\bar{R}_{t}\right)\left(\mathbb{1}_{a=A_{t}}-\pi_{t}(a)\right) &\text { for all } a \end{aligned} $$

$a$에 따라 나누어 포현하면 다음과 같다.

$$ \begin{aligned} H_{t+1}\left(A_{t}\right) & \doteq H_{t}\left(A_{t}\right)+\alpha\left(R_{t}-\bar{R}_{t}\right)\left(1-\pi_{t}\left(A_{t}\right)\right), & & \text { and } \cr H_{t+1}(a) & \doteq H_{t}(a)-\alpha\left(R_{t}-\bar{R}_{t}\right) \pi_{t}(a), & & \text { for all } a \neq A_{t} \end{aligned} $$

여기서 $ \alpha $는 step-size parameter이고 $\bar{R}_{t} \in \mathbb{R}$는 time step $t$이전까지의 평균보상이다. 따라서 위의 업데이트식은 incremental하게 적용할 수 있다. 식을 통해 time step $t$에서 선택한 action이 baseline보다 컸다면 해당 행동의 preference는 증가하고 나머지 action에 대해서는 감소할 것임을 알 수 있다. 반대로 선택한 action이 baseline보다 작았다면 해당 행동의 preference는 감소하고 나머지 행동의 preference는 증가하게 만들어준다. 위 식에서 각각 뒤에 붙는 $\left(1-\pi_{t}\left(A_{t}\right)\right)$와 $\pi_{t}(a)$는 모든 행동에 대한 preference의 총 합은 변하지 않도록 해준다는 관점에서 보면 이해가 편하다.

Performance

그렇다면 gradient bandit algorithm의 성능은 어떨까? 앞서와 마찬가지로 10-armed bandit에 대한 성능을 살펴보자. 이번에는 앞의 testbed와는 다르게 10개의 bandit 각각의 실제 기댓값은 평균이 0이 아닌 4인 정규분포에서 정해진다. (분산은 1로 동일) 따라서 모든 bandit에 대한 기대보상이 상향되는 결과를 가져올 것이다. 하지만 gradient bandit은 baseline term이 몇번의 시도 뒤에 +4에 가까운 값으로 설정되어 전체적으로 향상된 reward의 영향을 받지 않고 optimal action을 더 잘 추정할 수 있다.

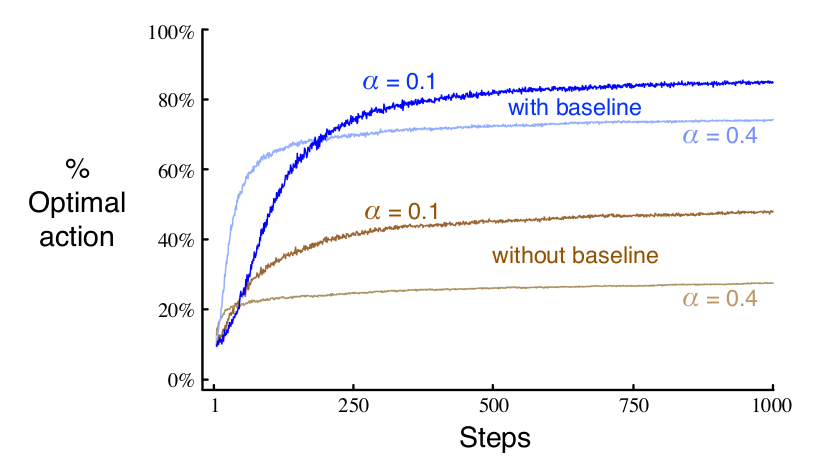
위의 그림을 보면 우선 with baseline과 without baseline을 통해 baseline term이 있는 경우 optimal action을 훨씬 빠르게 찾는다는 것을 볼 수 있다. 그리고 step-size parameter가 클수록 더 빠르게 수렴하는 것을 볼 수있다. 동시에, step-size parameter가 더 높아진다고 해서 optimal action 비율이 더 높아짐을 보장하지 않는다는 것 또한 볼 수 있다.

2.9 Asssociative Search (Contextual Bandits)

지금까지 다룬 bandit 문제는 모두 nonassociative task에 속한다. 그렇다면 무엇이 연관되지 않았다는 걸까? 상황에 따라 다른 행동이 연관된어 있지 않다는 것을 의미한다. Stationary와는 구분해서 생각해야한다. Nonassociative문제에서는 stationary일때, 최적인 하나의 action을 찾는 문제가 되고, nonassociative & nonstationary라면 시간이 지남에 따라 최적의 action을 잘 추적하는 방식을 찾으면 된다. 여기서 bandit의 상황은 고정이 되어 있다는 점에 유의해야한다. Bandit의 상태는 1개이다. (one-step MDP) 실제 강화학습 문제는 한번의 상황으로 끝나는 경우는 거의 없다. 강화학습이 다루는 중요한 주제가 sequential decision making이라는 점만 보아도 강화학습이 다루는 문제의 영역은 한 개 이상의 상황을 다룰 것임을 짐작할 수 있다.

그렇다면 bandit문제를 어떻게 하면 associative한 문제로서 생각해볼 수 있을까? 좀 특이한 bandit을 생각해보자. $k$-armed bandit이 있기는 한데 bandit을 직접 볼 수는 없고 어떤 화면이 있어서 화면을 통해 bandit을 보게 된다. 문제는 보고 있는 bandit이 어떤 bandit인지는 모른다. 그리고 화면을 보고 어떤 bandit을 당길지를 결정해야한다고 해보자. 매 step 내가 보는 화면의 bandit이 이전 step과 같은 bandit인지 아닌지 구분할 방법이 없는 상태인 것이다. 이렇게 되면 행동가치든, preference든 추정한 값을 어디에 배정해야될지 모른다는 문제가 생긴다. 여기서 조건을 약간 느슨하게해보자. Bandit마다 다행히 모두 똑같은 화면은 아니라고 가정해보자. 예를 들어 1번 bandit 화면이 보여질때는 약간 푸르딩딩하고 4번 bandit의 화면이 보여질때는 누리끼끼한 것처럼 단서들이 주어진다고 해보자. 이러면 하나의 화면을 보고 결정하더라도 지금 보고있는 화면의 색깔에 따라 bandit을 추정해볼 수 있고 그에 맞는 정책을 취할 수 있게 된다. 화면의 색깔에 따라 다른 행동을 선택해야하는 이 상황이 associative한 상황이다. 즉, 화면의 색깔(상태)과 행동이 연관되게 된다. 이러한 문제는 시행착오를 통해 상황에 따라 최적의 행동을 탐색해야하는 associative search 문제가 되는 것이다. 문맥이 생겼다는 의미에서 contextual bandits라고 부르기도 한다.

그렇다면 이러한 associative search task는 full reinforcement learning problem 문제라고 할 수 있을까? 그렇지는 않다. 교재에서 associative search는 full reinforcement learning과 $k$-armed bandits의 중간에 있다고 말한다. 상황에 따라 action을 최적화해야하는, 즉 policy학습 개념을 포함하기는 하지만 여전히 bandit 문제는 즉각적인 보상만 고려하면 되는 one-step MDP이기 때문이다. 행동이 보상을 주는 것뿐만 아니라 다음 상황에도 영향을 준다면, 그 때 비로소 full reinforcement learning 문제가 된다.

2.10 Summary

이번 문서에서는 bandit문제를 바탕으로 강화학습의 기본적인 개념인 exploration-exploitation balancing과 이에 대한 기법인 $\varepsilon$-greedy 방법을 보았다. 또한 성능향상을 위한 trick으로 optimistic inital value나 UCB와 같은 방법을 알아보았으며 마지막으로 행동가치가 아닌 preference를 추정하는 gradient bandit algorithm과 associative 문제의 정의를 보았다.

문제에 따라 다르겠지만 교재에서는 그렇다면 10-armbed bandit testbed에 대해서 어떤 방법이 가장 효과적이었는지를 비교해준다. 아래의 그래프는 이번 장에서 다룬 방법들에 대해 parameter변화에 따른 평균보상을 보여준다. 이와 같은 그래프를 parameter study라고 한다.

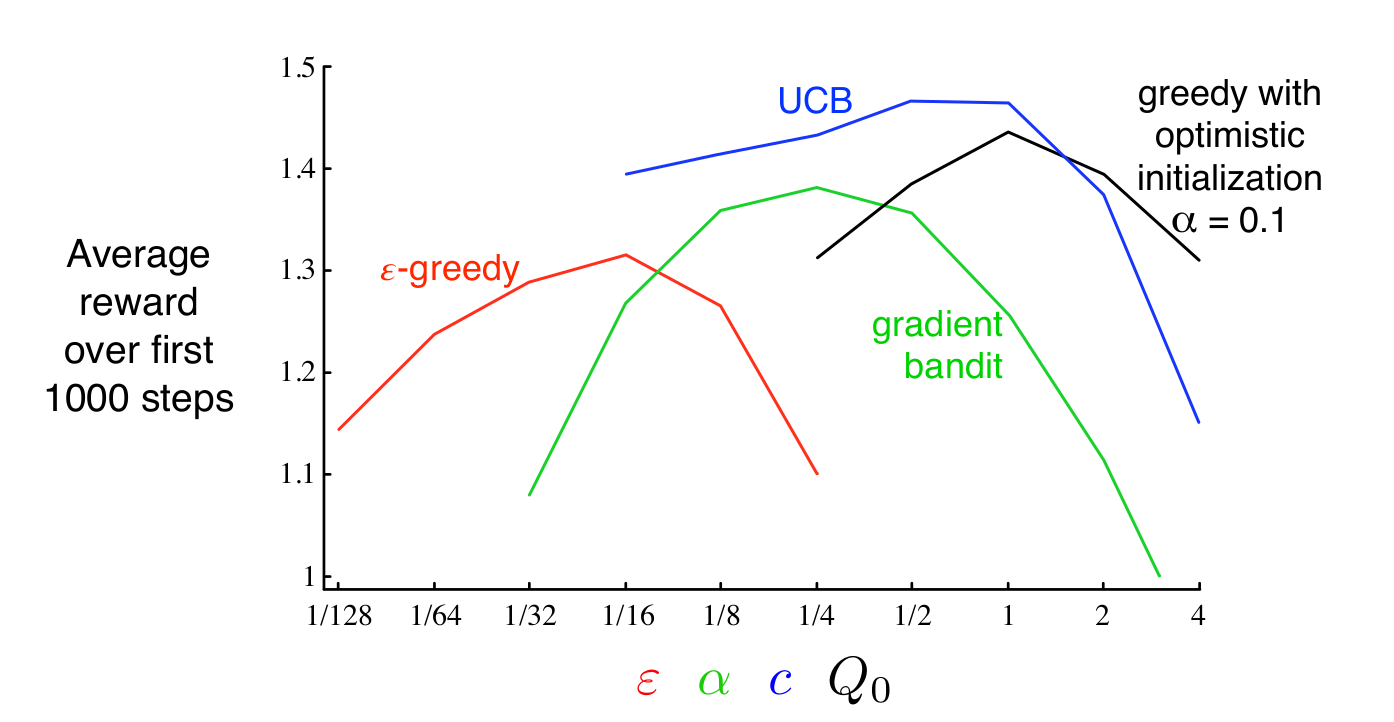
10-armed testbed에서는 UCB가 전반적으로 가장 잘 작동하는 양상을 보인다. 교재에서는 이번 장에서 다룬 알고리즘들은 매우 단순하지만 그만큼 가정과 복잡성이 단순해 SOTA로 충분히 가치가 있다고 말한다. 이후에 더 복잡한 방식들을 다루게 되겠지만 그런 방법들은 더 강한 가정을 필요로하며 이로 인해 full reinforcement learning에 적용하기 어렵다는 한계 또한 존재한다. 이후 full reinforcement learning 문제를 푸는 방법에서도 이번 문서에서 다룬 기법들을 부분적으로 사용하게 된다.

$k$-armed bandit 문제에서 exploration exploitation balancing을 다루는 방법 중 하나로 행동가치의 특수한 형태인 Gittins index를 활용할 수도 있다. 일반적으로는 가능하지 않지만 문제의 prior 분포에 대해 완전한 정보(complete knowledge)가 있을 경우에 Gittins index를 사용하면 tractable하며 optimal solution을 직접적으로 구할 수 있게된다. 하지만 full reinforcement learning 문제로 확장이 어렵다는 문제가 있다.

Gittins index 자체는 Bayesian 방법의 하나로, 행동가치에 대한 초기 분포와 이른 매 step마다 update하는 방법을 사용한다. 일반적으로 이 과정은 연산하기가 매우 까다로우나 conjugate prior를 사용하는 경우에 한해서는 효율적인 update가 가능하다. 일단, 이렇게 행동가치에 대한 posterior분포가 계산되면 행동의 posterior 분포에서 각각 sampling을 하고 그 중 가장 큰 값을 사용한 결과로 update한다. 이러한 방식을 posterior sampling 또는 Thomson sampling이라고 한다.

Bayesian setting을 사용하면 행동가치 뿐만이 아니라 exploration과 exploitation의 optimal balance를 계산하는 것도 생각해 볼 수 있다. 가능한 행동 각각에 대해서 즉각적인 보상과 행동가치에 대한 posterior 분포를 계산할 수 있으며 이 과정에서 update되는 posterior분포는 문제에 대한 information state가 된다. 예를 들어 1000개의 sequnetial decision making 문제가 있을 때, 각 step에 대해서 모든 행동, 보상을 계산할 수 있을 것이다. 그림으로 그려보면 매우 큰 tree를 그려가는 것으로 비유할 수 있다. 가정을 추가하면, 보상과 각 사건에 이르는 확률까지도 계산할 수 있게 된다. 하지만 다시 생각해보면, 이렇게 큰 tree를 완성하는 것이 가능할까? 이렇게 가능한 모든 경우를 고려할 때, tree는 매우 빠르게 커지게 된다. 1000개의 step이 각 step에서 두 개의 행동과 두 개의 보상값만 가진다 하더라도 tree는 $2^{2000}$개의 leaf를 갖는다. 결론적으로 모든 경우에 대해서 일일히 계산하는 접근은 현실적으로 불가능하다. 이에 대한 대안은 효율적으로 근사를 시켜보는 것이다. 이러한 근사를 도입하게 되면 bandit 문제는 full reinforcement learning 문제로 바뀌게 되며, Part 2에서 소개되는 approximated reinforcement learning 방법을 사용할 수 있게 된다.

Reference

• Sutton, R. S., Barto, A. G. (2018). Reinforcement learning: An introduction. Cambridge, MA: The MIT Press.